Просмотр содержимого документа
«Конспект урока по алгебре в 8 классе "Сложение и вычитание дробей с разными знаменателями"»
Правило сложения и вычитания дробей
с одинаковыми знаменателями
Ход урока
I. Организационный момент.
II. Устная работа.
– Вычислите:
а) 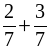 ; б)
; б)  ; в)
; в) 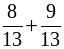 ; г)
; г)  ;
;
д)  ; е)
; е) 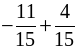 ; ж)
; ж) 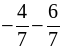 ; з)
; з)  .
.
III. Объяснение нового материала.
Устная работа дает возможность актуализировать знания учащихся о сложении и вычитании обыкновенных дробей с одинаковыми знаменателями.
После этой работы следует сообщить учащимся, что рациональные дроби с одинаковыми знаменателями складываются и вычитаются по тем же правилам, которые учащиеся способны сформулировать самостоятельно.
После формулировки правил на доску выносится их буквенная запись:
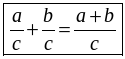 и
и 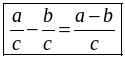 .
.
Далее следует рассмотреть примеры 1–3 из учебника. Вопрос о сложении и вычитании дробей с противоположными знаменателями целесообразно рассмотреть на следующем уроке.
IV. Формирование умений и навыков.
1. № 53, № 55, № 57.
При вычитании дробей учащиеся могут допускать распространенную ошибку: не учитывать, что «минус» перед дробью вносится в числитель, и неправильно расставлять знаки.
Поэтому важно следить, чтобы первое время учащиеся вели подробные записи.
№ 57.
в) 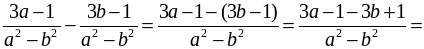
= 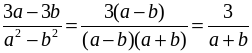 .
.
2. № 58 (а), № 59 (а).
3. № 60.
Р е ш е н и е

= 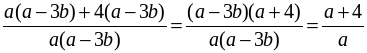 .
.
При а = –0,8 дробь 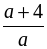 равна –4, то есть данное в условии значение b является лишним.
равна –4, то есть данное в условии значение b является лишним.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Сформулируйте правило сложения рациональных дробей с одинаковыми знаменателями.
– Сформулируйте правило вычитания рациональных дробей с одинаковыми знаменателями.
Домашнее задание: № 54, № 56, № 59 (б)
Сложение и вычитание дробей
с противоположными знаменателями
Цели: формировать умение складывать и вычитать рациональные дроби с противоположными знаменателями.
Ход урока
I. Организационный момент.
II. Устная работа.
– Вычислите:
а) 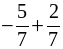 ; д)
; д)  ;
;
б) 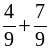 ; е)
; е) 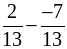 ;
;
в)  ; ж)
; ж) 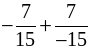 ;
;
г) 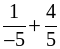 ; з)
; з)  .
.
III. Объяснение нового материала.
Сначала необходимо, чтобы учащиеся вспомнили следствие из основного свойства дроби, и предложить им выполнить задание, в котором нужно поменять знак числителя или знаменателя рациональной дроби.
а) 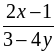 ; в)
; в) 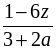 ;
;
б) ; г) .
Затем продемонстрировать пример 4 из учебника и сделать вывод о том, как сложить или вычесть две рациональные дроби с противоположными знаменателями.
IV. Формирование умений и навыков.
1. Выполните сложение или вычитание дробей:
а)  ; в)
; в)  ;
;
б)  ; г) .
; г) .
2. № 61, № 63.
3. Преобразуйте выражение:
а) ;
б) ;
в) ;
4. № 66.
5. № 68.
Р е ш е н и е
.
Полученное выражение принимает натуральные значения, если дробь  является натуральным числом, то есть когда 6 делится на п. Значит, п = 1; 2; 3; 6.
является натуральным числом, то есть когда 6 делится на п. Значит, п = 1; 2; 3; 6.
О т в е т: 1; 2; 3; 6.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Сформулируйте правило сложения и вычитания рациональных дробей с одинаковыми знаменателями.
– Как выполнить сложение или вычитание рациональных дробей, знаменатели которых являются противоположными выражениями?
Домашнее задание: № 62, № 64






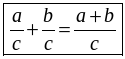 и
и 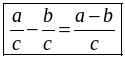 .
.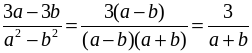 .
.
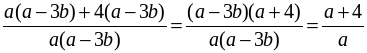 .
.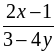 ; в)
; в) 









