Логические формулы и функциональные схемы сумматоров
ПОНЯТЬ
Функциональную схему устройства удобнее всего строить по его логической формуле. Но в реальной практике логическая формула часто изначально неизвестна, зато легко построить таблицу истинности.
Вспомним модель «чёрного ящика». Подавая на входы поочерёдно все возможные комбинации сигналов и записывая сигналы, полученные на выходе, можно получить таблицу истинности любого конечного автомата.
Иногда таблица истинности логично вытекает из условия задачи.
Пример
На олимпиаду по информатике нужно отобрать задания из предложенного списка. Три эксперта по каждому заданию высказывают своё мнение – лёгкое оно (0) или трудное (1). Задание остаётся для последующего обсуждения (1), если ровно два эксперта оценили её как трудную.
Автоматизированная система голосования моделируется следующей таблицей истинности.
| Входы | Выход |
| X | Y | Z | Результат F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 * |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 * |
| 1 | 1 | 0 | 1 * |
| 1 | 1 | 1 | 0 |
Важно, что и формула алгебры логики, и соответствующие ей таблица истинности и функциональная схема являются информационными моделями. Причем все эти модели взаимозаменяемы: зная логическую формулу можно легко построить таблицу истинности и функциональную схему. По функциональной схеме можно восстановить формулу и таблицу истинности. Очевидно, что и от таблицы истинности можно перейти к логической формуле и функциональной схеме.
Приведем один из способов построения логической формулы по таблице истинности. Рассмотрим его на примере таблицы истинности устройства для голосования, описанной в примере.
В устройстве будет 3 входа - Х, Y, Z (n=3) и один выход (F).
1 шаг. Отмечаем те строки, значение F в которых равно 1. В нашем случае таких строк три (m=3).
2 шаг. Для каждой отмеченной строки записываем конъюнкцию всех переменных-входов. Причём, если в соответствующей строке значение какой-либо переменной равно 0, то добавляем к переменной операцию отрицания. В нашем случае получаем: 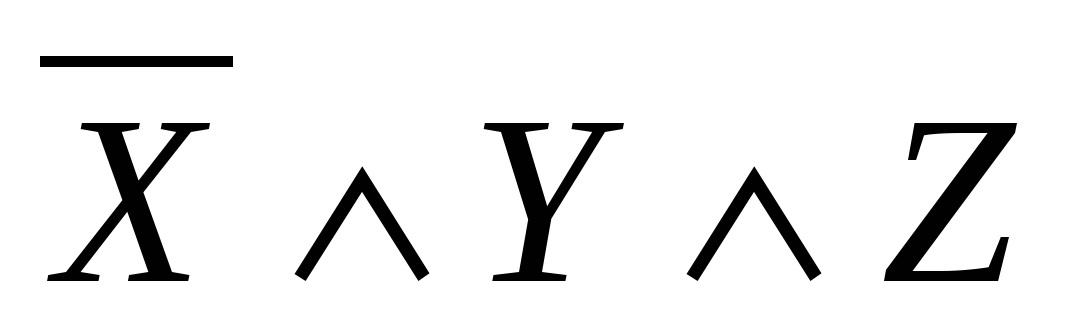 ,
, 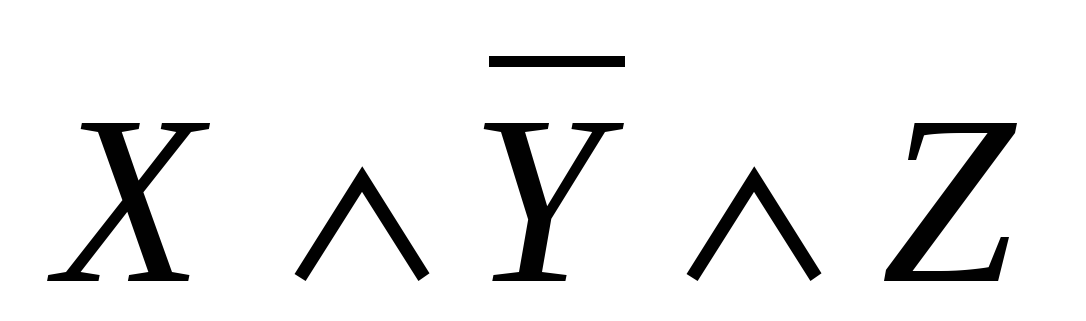 ,
, 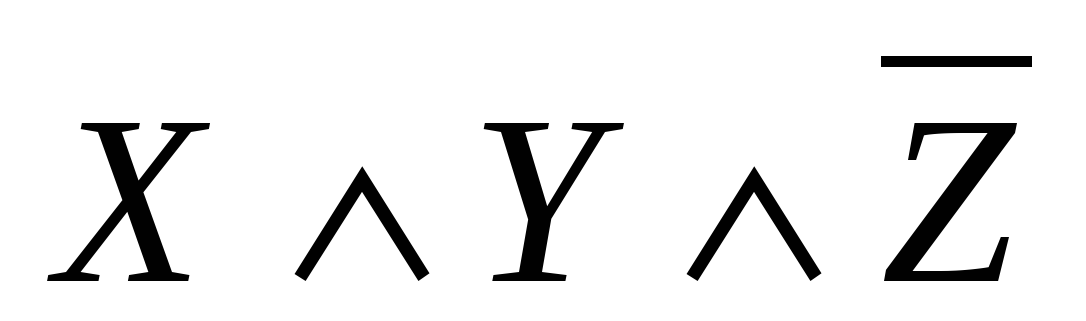 .
.
3 шаг. Объединяем полученные конъюнкции операцией дизъюнкции. Получаем: 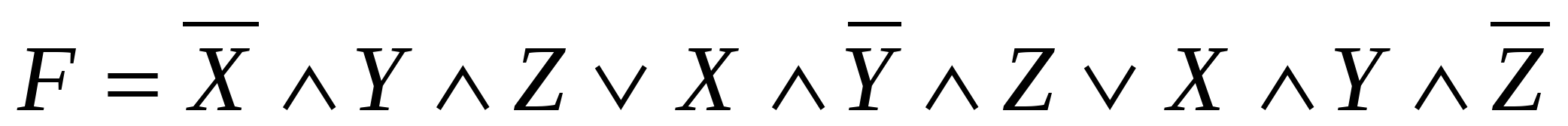 .
.
Итоговая формула содержит дизъюнкцию m конъюнкций, в каждую из которых входят все n переменных с отрицанием или без него. Заметим, что построенная таким образом формула называется в математике совершенной дизъюнктивной нормальной формой (СДНФ).
При решении практических задач полученная СДНФ максимально упрощается с помощью законов алгебры логики, и функциональная схема устройства строится уже по упрощенному варианту, который эквивалентен исходной СДНФ.
Рассмотрим, как осуществляется сложение двоичных чисел в арифметико-логическом устройстве процессора.
Пусть надо сложить два двоичных числа Х=10112 и Y=11012.
1 1 1 1 - перенос
10112 - первое слагаемое
11012 - второе слагаемое
110002 - сумма
В результате мы получим число 110002.
При сложении нам пришлось делать переносы в первый, второй, третий и четвертый разряды.
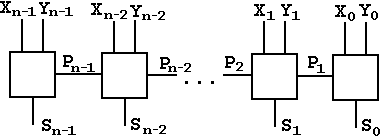
Обозначив цифры первого слагаемого X3X2X1X0, цифры второго слагаемого Y3Y2Y1Y0, переносы в следующий разряд Р4Р3Р2Р1 и сумму S4S3S2S1S0 можно схематично представить суммирование так:
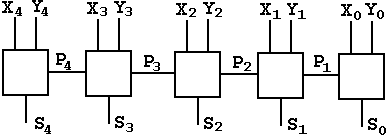
Рис. Схема 5-разрядного автомата для сложения двух двоичных кодов
Крайний правый элемент в схеме суммирующего автомата имеет два входа (X0 и Y0) и два выхода (S0 и Р1). Этот элемент называется полусумматором.
Устройства для суммирования разрядов с первого и дальше имеют три входа (Xk, Yk, Pk) и два выхода (Sk и Рk+1). Называются они сумматорами на три входа.
Обратите внимание, что схема даёт наглядное представление о том, как возникает переполнение при сложении кодов чисел: у суммирующего элемента старшего разряд нет переноса в следующий разряд, то есть этот сигнал «теряется».
Построим функциональную схему полусумматора. Для этого вначале составим таблицу истинности и по ней – логическую формулу. Таблицу истинности полусумматора построим в соответствии с правилами двоичной арифметики
| Входы | Выходы |
| Х0 | Y0 | Р1 | S0 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
По данной таблице истинности построим логические формулы:
P1 = X0Y0
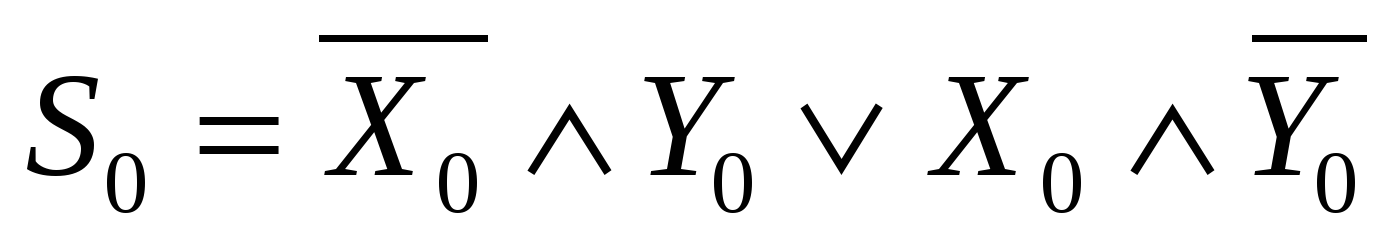 . После преобразований по законам алгебры логики получим
. После преобразований по законам алгебры логики получим 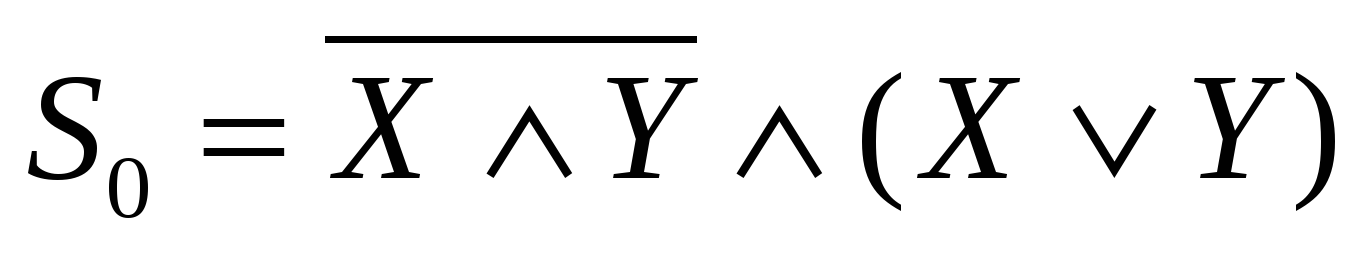
Функциональная схема полусумматора, построенного по данным формулам, имеет вид
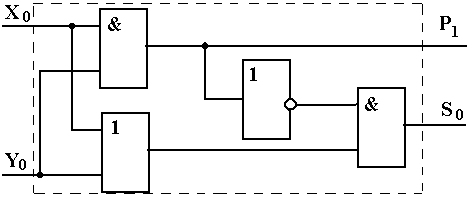
Аналогично сроятся таблица истинности, логическая формула и функциональная схема сумматора на три входа.
Таблица истинности сумматора на три входа
| Входы | Выходы |
| Xk | Yk | Pk | Pk+1 | Sk |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Логические формулы сумматора на три входа (СДНФ, ПОСТРОЕННАЯ ПО ТАБЛИЦЫ ИСТИННОСТИ, и после упрощения по законам алгебры логики; индексы k не указаны):
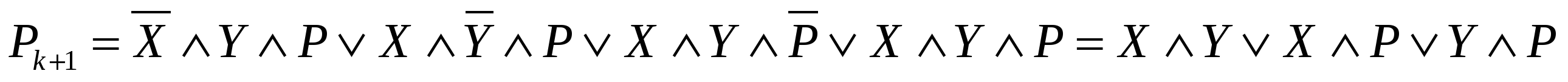
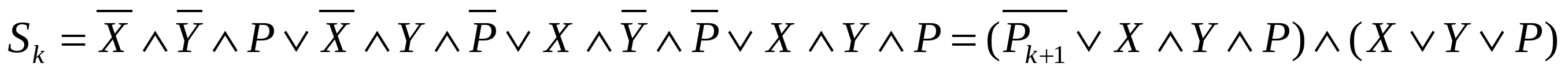
Обратите внимание, что формулы симметричны относительно x, y, p, то есть все входы «равноправны».
ЗНАТЬ
Таблица истинности, логическая формула и функциональная схема – взаимозаменяемые информационные модели устройства.
Таблицу истинности конечного автомата можно построить, исходя из условий задачи, или проведя эксперименты, рассматривая автомат как «чёрный ящик».
Если известна таблица истинности работы какого-либо устройства, в которой представлены все возможные значения входов и соответствующие им значения выходов, то можно построить логическую формулу (совершенную дизъюнктивную нормальную форму) по следующему алгоритму:
отметить все «1» в столбце выхода, пусть их будет m;
для каждой отмеченной строки выписываем логическое произведение (конъюнкцию) всех n переменных, причём, если в данной строке значение какой-то переменной равно «0», то записываем её со знаком отрицания (инверсии);
объединяем полученные произведения с помощью логического сложения (дизъюнкции);
упрощаем полученную формулу (совершенную дизъюнктивную нормальную форму) по законам алгебры логики, если это возможно.
N-разрядный автомат для сложения двух двоичных кодов состоит из одного полусумматора и n-1 сумматора на три входа.
Модели полусумматора:
| Таблица истинности | Функциональная схема | Логические формулы |
| Входы | Выходы | | Х0 | Y0 | Р1 | S0 | | 0 | 0 | 0 | 0 | | 0 | 1 | 0 | 1 | | 1 | 0 | 0 | 1 | | 1 | 1 | 1 | 0 |
|  |
P1 = X0Y0
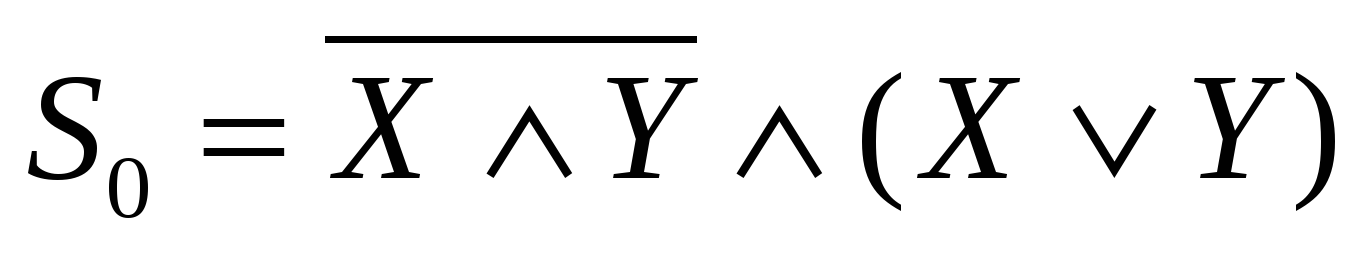
|
УМЕТЬ
Постройте функциональную схему сумматора на три входа (обратите внимание, что у дизъюнкторов и конъюнкторов может быть более двух входов).
Постройте таблицу истинности, логическую формулу и функциональную схему устройства, которое проверяет, попадает ли t в интервал (-∞,0) (10, 20). Переменные-входы пусть соответствуют значениям истинности следующих суждений: Х = «tY= «tZ= «t
В комнате находится люстра и два выключателя, размещенные в разных местах комнаты. Построить таблицу истинности, логическую формулу и функциональную схему устройства, которое будет регулировать работу люстры по такому правилу: нажатие на любой выключатель включает люстру, если она была выключена, и выключает люстру, если она была включена (обратите внимание, что это пример автомата «с памятью», сигнал на выходе которого зависит не только от сигналов на входах, но и от состояния самого устройства).
***В параграфе, посвященном моделям кибернетики, рассматривался пример кибернетической системы «Умный отец». Постройте логическую формулу и функциональную схему автоматического устройства по приведённой там таблице.
5
































