Математика. Герона треугольник.

Герона треугольник — треугольник, длины сторон и площадь которого выражаются целыми числами. Назван по имени греческого математика Герона Александрийского (ок. I в. н. э.), рас- смотревшего треугольники со сторонами 13, 14, 15 и 5, 12, 13, площади которых соответственно равны 84 и 30.

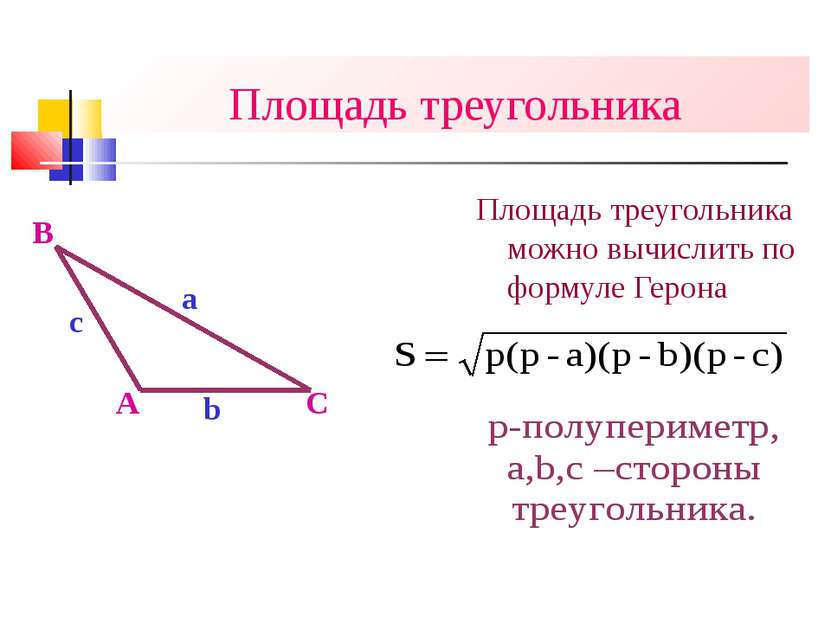
Геронов треугольник – треугольник, длины всех трех сторон и площадь которого выражаются рациональными числами. Интересна задача о нахождении всех героновых треугольников. Домножая длины сторон такого треугольника на соответствующий общий множитель, можно получить подобный треугольник с целочисленными сторонами и площадью, поэтому по формуле Герона эта задача сводится к решению в целых числах a, b, c, S уравнения:

S² = p(p – a)(p – b)(p – c), где p = (a + b + c) / 2.

Брахмагупта нашел его решение в параметрическом виде: длины сторон целочисленного геронова треугольника равны k(m² + n²), n(m² + k²), (n + k)(m² – nk), где k, m, n – произвольные натуральные числа, причем m² > nk; при этом площадь равна kmn(m + n)(m² – nk). Несколько примеров: (3, 4, 5), (5, 5, 6), (5, 5, 8), (6, 8, 10), (10, 10, 12), (5, 12, 13), (10, 13, 13), (9, 12, 15), (4, 13, 15), … . Заметим, что все эти примеры, кроме последнего, – т.н. «пифагоровы треугольники», т.е. прямоугольные треугольники с рациональными сторонами или равнобедренные треугольники, состоящие из двух равных пифагоровых. Треугольник из последнего примера состоит из двух неравных пифагоровых треугольников со сторонами (12/5; 16/5, 4) и (16/5, 63/5, 13) с общим катетом длины 16/5. Нетрудно показать, что любой геронов треугольник либо прямоугольный (пифагоров), либо составлен из двух пифагоровых.