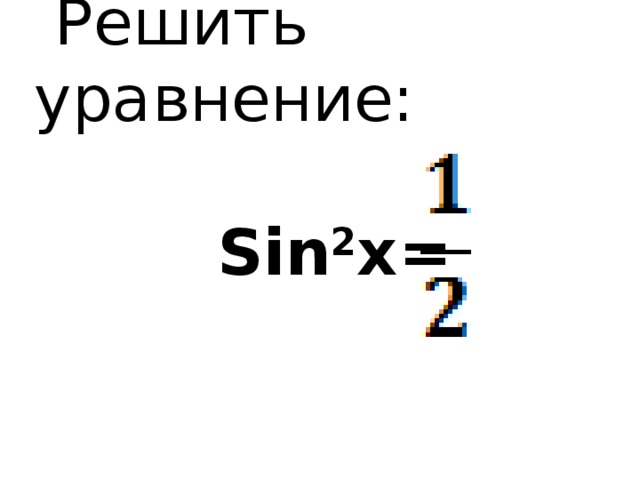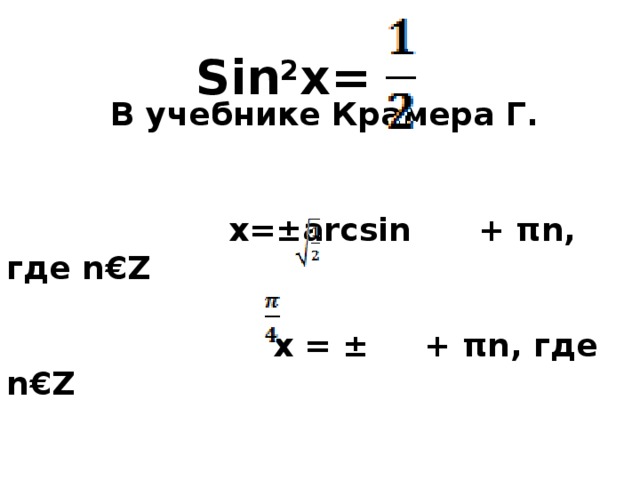Обобщающий мастер-класс по теме:«Задания для подготовки к ЕГЭ. Решение тригонометрических уравнений (задание №13)»

Обобщающий мастер-класс по теме: «Задания для подготовки к ЕГЭ. Решение тригонометрических уравнений (задание №13)»

Автор:

Набиева Роза Мусаевна,

учитель математики высшей квалификационной категории

МКОУ СОШ №4

г. Южно-Сухокумск

Ян Амос Коменский

Чешский педагог

История тригонометрии

Тригонометрия - с греч. измерение треугольников. Возникла тригонометрия в результате решения задач, связанных с землемерием, астрономией и строительным делом. Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (II в. до н. э.) и Клавдием Птолемеем (II в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями. Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII в. Леонардом Эйлером (1707-1783гг.). Дальнейшее развитие теории было положено в XIX в. Н. И. Лобачевским и другими учёными.

Актуальность темы:

• Знания тригонометрии применяются во многих областях науки;
• Изучение тригонометрии помогает развить логику, нестандартное мышление человека;
• Затрачивается огромное количество различных ресурсов человека на решение тригонометрических уравнений, поэтому методы и способы их решения необходимо систематизировать;
• Тригонометрические уравнения из года в год встречаются среди заданий ЕГЭ;
• В школьной программе отводится мало времени на изучение данной темы;
• Уравнения повышенной сложности изучаются на факультативных занятиях в ознакомительном порядке.

ЦЕЛЬ РАБОТЫ:

Систематизировать, обобщить, расширить знания и умения, связанные с применением методов решения тригонометрических уравнений

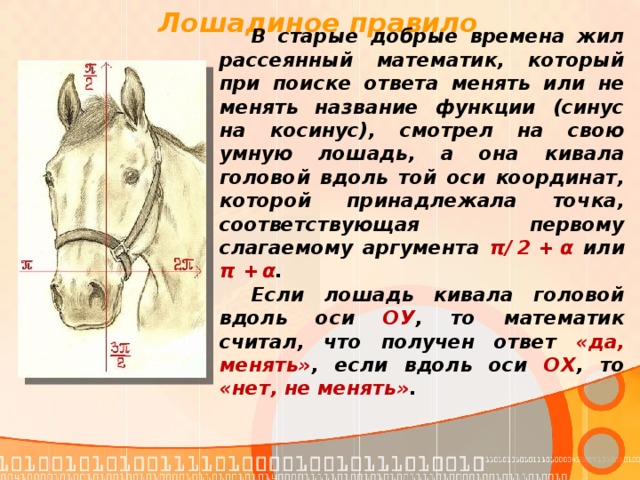
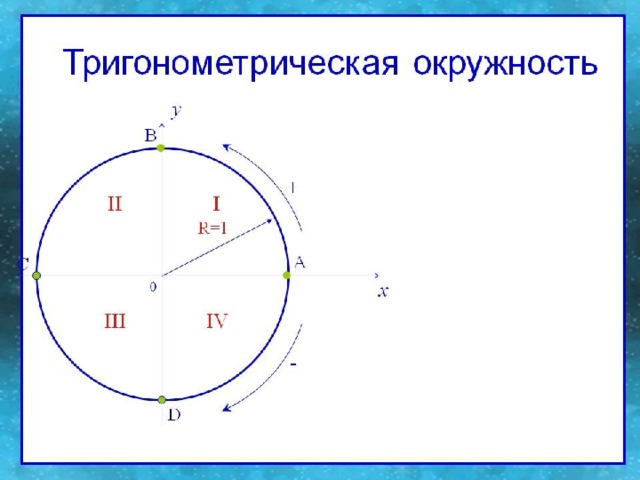
Лошадиное правило

В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции (синус на косинус), смотрел на свою умную лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/ 2 + α или π + α .

Если лошадь кивала головой вдоль оси ОУ , то математик считал, что получен ответ «да, менять» , если вдоль оси ОХ , то «нет, не менять» .

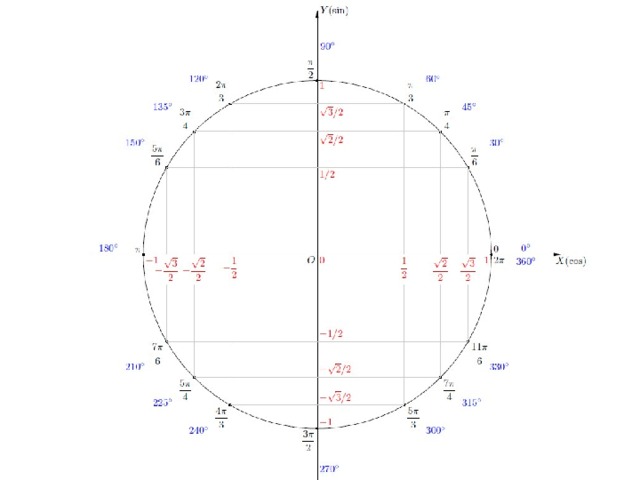
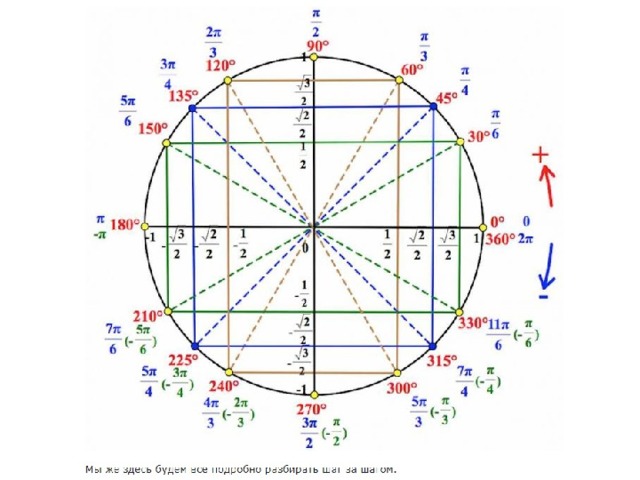
Очень часто требуется знать наизусть значения cos , sin , tg , ctg для углов 0° , 30° , 45° , 60° , 90° .

Но если вдруг какое-либо значение забудется, то можно воспользоваться правилом руки.

Правило: Если провести линии через мизинец и большой палец, то они пересекутся в точке, называемой “лунный бугор”.

Мнемоническое правило “Тригонометрия на ладони”

Образуется угол 90° . Линия мизинца образует угол 0° .

Проведя лучи из “лунного бугра” через безымянный, средний, указательный пальцы, получаем углы соответственно 30° , 45° , 60° .

Подставляя вместо n : 0 , 1 , 2 , 3 , 4 , получаем значения sin , для углов 0° , 30° , 45° , 60° , 90° .

Для cos отсчет происходит в обратном порядке.

Функция у = sin x.

1. Областью определения функции является множество

всех действительных чисел ( R )

2. Областью значений [ - 1; 1 ].

3. Функция у = sin α нечетная, т.к. sin (- α) = - sin α

4. Функция периодическая, с главным периодом 2π

Функция у = соs x.

1. Областью определения функции является множество

всех действительных чисел ( R )

2. Областью изменений (Областью значений) - [ - 1; 1 ]

3. Функция у = cos α четная, т.к. cos (- α) = cos α

4. Функция периодическая, с главным периодом 2π.

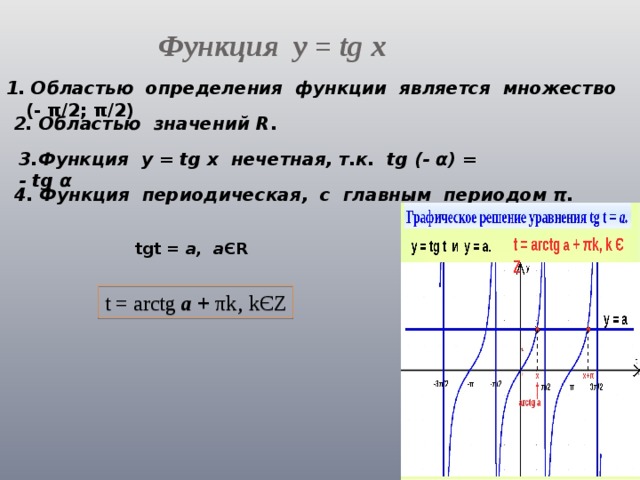
Функция у = tg x

1. Областью определения функции является множество (- π/2; π/2)

2. Областью значений R .

3.Функция у = tg x нечетная, т.к. tg (- α) = - tg α

4. Функция периодическая, с главным периодом π.

tgt = а, а ЄR

t = arctg а + πk‚ kЄZ

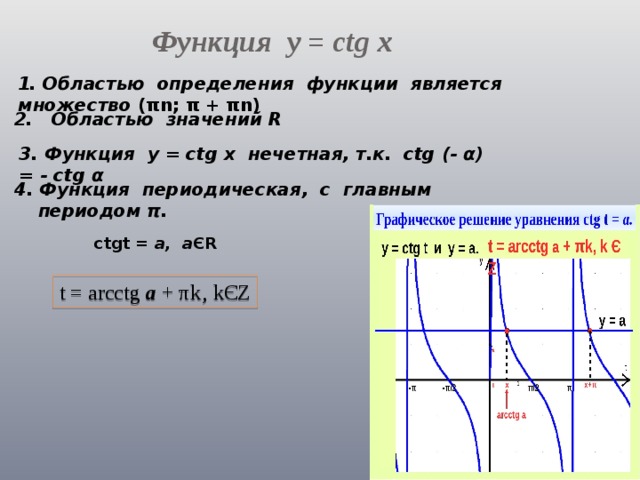
Функция у = ctg x

1. Областью определения функции является множество (πn; π + πn)

2. Областью значений R

3. Функция у = ctg x нечетная, т.к. ctg (- α) = - ctg α

4. Функция периодическая, с главным периодом π.

ctgt = а, а ЄR

t = arcctg а + πk‚ kЄZ

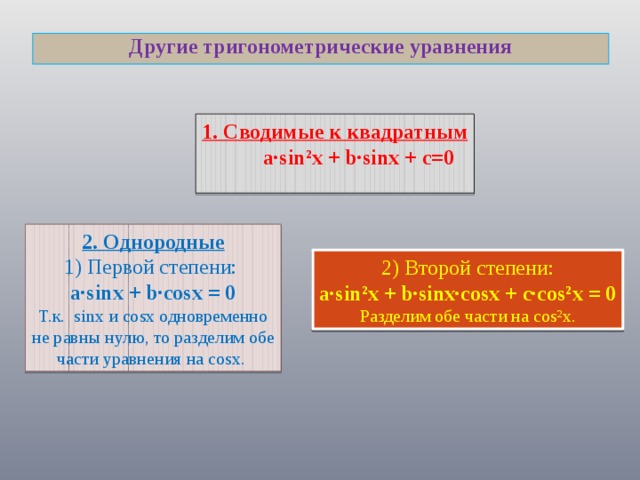
Другие тригонометрические уравнения

1. Сводимые к квадратным

a∙sin²x + b∙sinx + c=0

2. Однородные

1) Первой степени:

a∙sinx + b∙cosx = 0

Т.к. sinx и cosx одновременно

не равны нулю, то разделим обе

части уравнения на cosx.

2) Второй степени:

a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0

Разделим обе части на cos²x.

Содержание

• Метод замены переменной
• Метод разложения на множители
• С помощью тригонометрических формул:

• Формул сложения
• Формул приведения
• Формул двойного аргумента

Алгоритм решения уравнения графическим способом

• Привести уравнение к виду f(x)=g(x), где у=f(x) и у=g(x) известные нам функции.
• Построить графики функции у=f(x) и у=g(x).
• Отметить ВСЕ точки пересечения графиков.
• Найти абсциссы точек пересечения (это и есть корни уравнения).
• Записать ответ.

Разложение левой части уравнения на множители.

Решим функционально-графическим методом:

sin x – cos x = 1

sin x = cos x + 1

y = sin x – график синусоида

y = cos x + 1 – синусоида, смещенная на единицу вверх

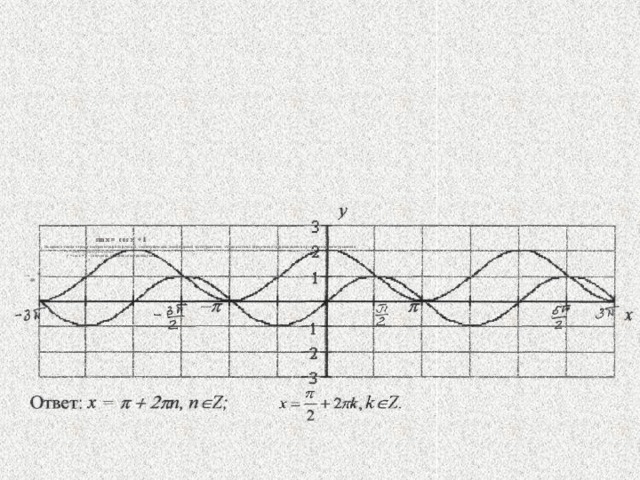
sin x = cos x + 1 На одном и том же чертеже построим графики функций, соответствующих левой и правой части уравнения. Абсциссы точек пересечения графиков являются решением данного уравнения, у = sin х - график синусоида. у = соs х + 1 – синусоида, смещённая на единицу вверх.

Решим аналитическим и графическим методами уравнение:

sin 2x – cos x = 0

2 sin x*cos x – cos x=0

cos x*(2 sin x – 1)=0

2 sin x – 1=0

или

cos x=0

sin x = 1/2

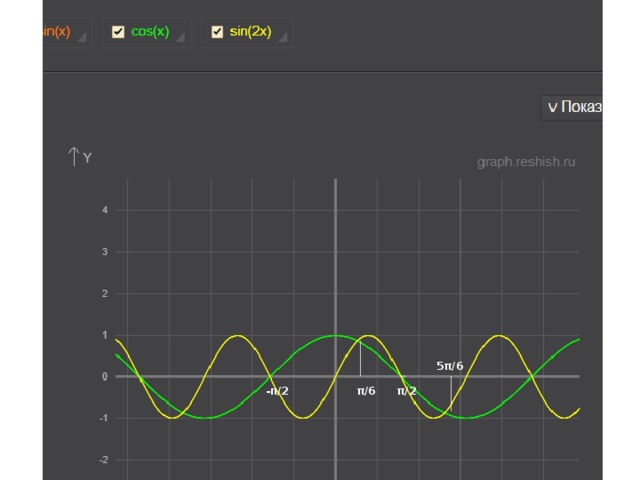
5π/6

π/6

π/2

-п/2

a) Решить уравнение 2 cos 2x + 4 sin (3π/2+x) – 1=0 б) Найти все корни, принадлежащие отрезку [- 3π; - π]

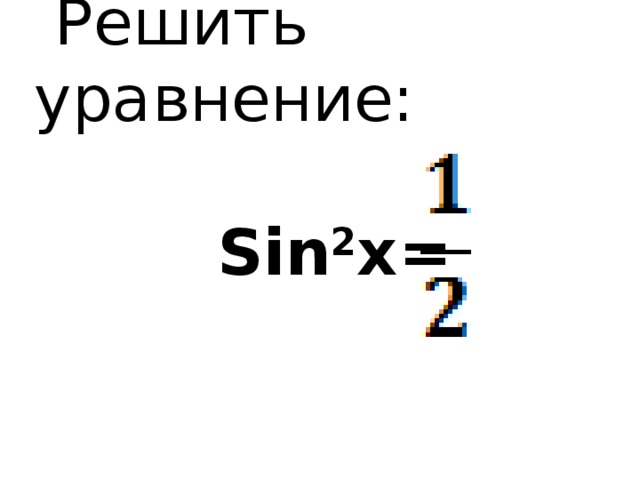
Решить уравнение: Sin 2 x=

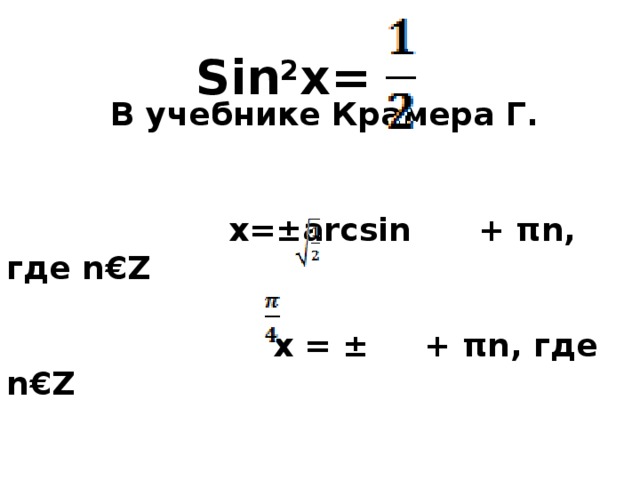
Sin 2 x=

В учебнике Крамера Г.

x=±arcsin + πn, где n€Z

x = ± + πn, где n€Z

Восемь способов решения одного тригонометрического уравнения.

1.Приведение уравнения к однородному.

2.Разложение левой части уравнения на множители.

3.Введение вспомогательного угла.

4.Преобразование разности (или суммы) тригонометрических функций в произведение.

5.Приведение к квадратному уравнению.

6.Возведение обеих частей уравнения в квадрат.

7.Универсальная подстановка.

8.Графическое решение.

Заключение

В своей работе я изучила историю возникновения и применение на практике знаний о тригонометрии. Повторила решения тригонометрических уравнений школьного курса и познакомилась с различными методами решения тригонометрических уравнений.

Кроме того, я исследовала классификацию уравнений по способу их решения, подобрала примеры уравнений, встречающихся на Едином государственном экзамене, и изучила способы отбора корней на заданном промежутке, на единичной окружности, методом неравенств.

« То, что мы знаем, - ограниченно, а то чего мы не знаем, - бесконечно». Пьер Лаплас:

Используемые источники:

• ЕГЭ: 4000 задач с ответами по математике . Все задания «Закрытый сегмент». Базовый и профильный уровни /И.В.Ященко, И.Р.Высоцкий, А.В.Забелин и др.; под редакцией И.В.Ященко. – М.: Издательство «Экзамен», 2016. – 640 с. (Серия «Банк заданий ЕГЭ»)
• Математика. ЕГЭ – 2013: экспресс – курс для подготовки к экзамену/ Дмитрий Гущин. – М, : Издательский дом «Учительская газета», 2013. – 256 с. (Библиотечка «Учительской газеты». Готовимся к ЕГЭ с лучшими учителями России)
• http://reshuege.ru /
• https://graph.reshish.ru/

СПАСИБО ЗА ВНИМАНИЕ