Окружность -подготовка к ОГЭ . Примеры решения задач.

Подготовка к ОГЭ.

Окружность.

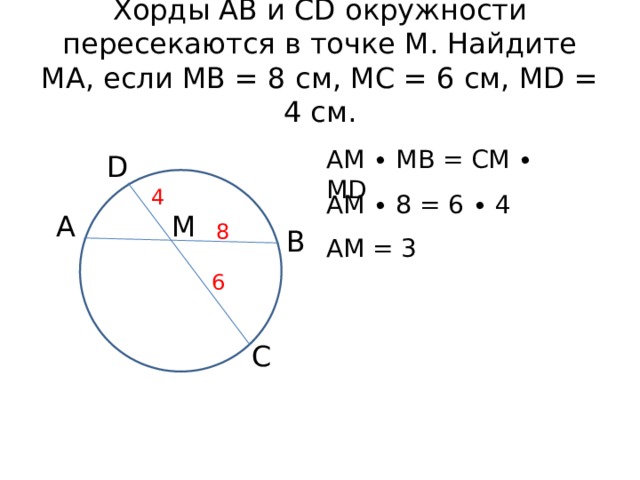
Хорды АВ и CD окружности пересекаются в точке М. Найдите МА, если МВ = 8 см, МС = 6 см, МD = 4 см.

AМ ∙ МВ = СМ ∙ MD

D

4

AМ ∙ 8 = 6 ∙ 4

А

M

8

В

AМ = 3

6

С

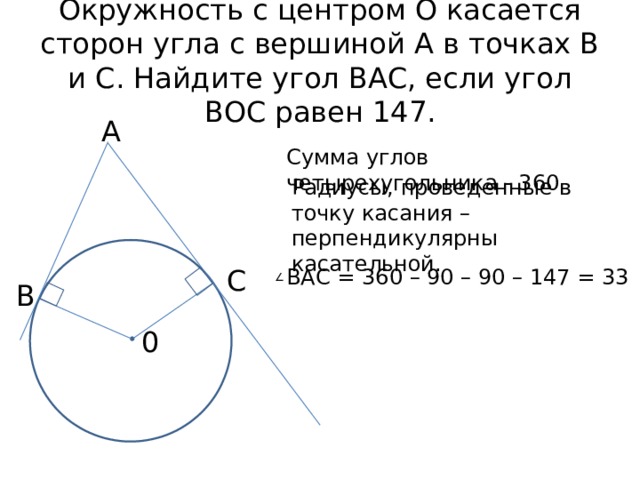
Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если угол ВОС равен 147.

А

Сумма углов четырехугольника - 360

Радиусы, проведенные в точку касания – перпендикулярны касательной.

С

ВАС = 360 – 90 – 90 – 147 = 33

В

0

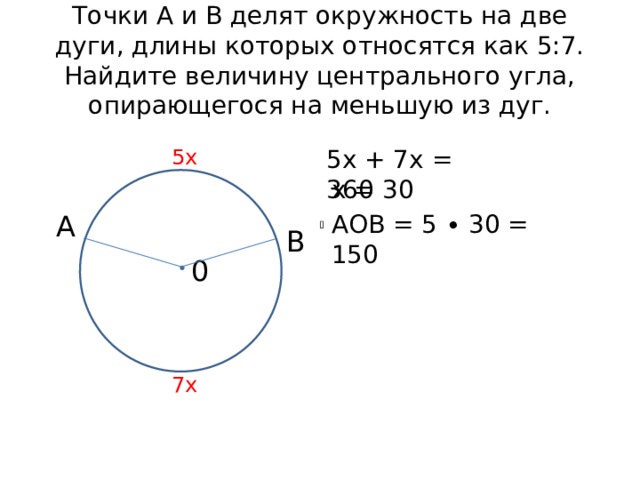
Точки А и В делят окружность на две дуги, длины которых относятся как 5:7. Найдите величину центрального угла, опирающегося на меньшую из дуг.

5х

5х + 7х = 360

х = 30

А

АОВ = 5 ∙ 30 = 150

В

0

7х

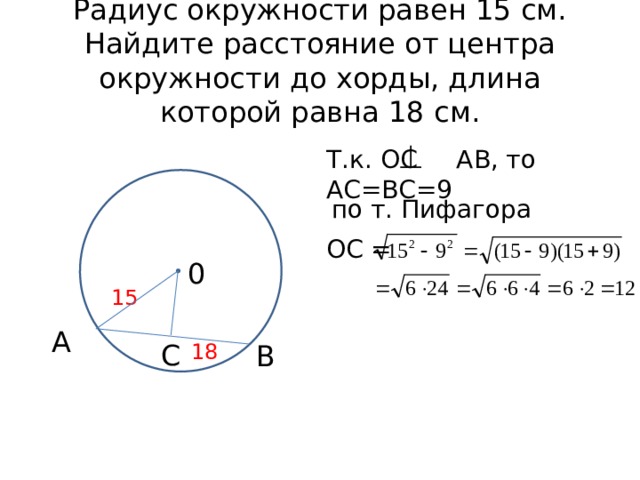
Радиус окружности равен 15 см. Найдите расстояние от центра окружности до хорды, длина которой равна 18 см.

Т.к. ОС АВ, то АС=ВС=9

по т. Пифагора

ОС =

0

15

А

С

18

В

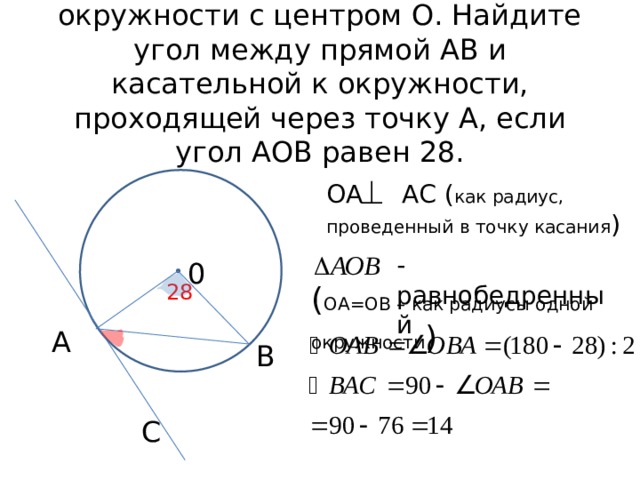
Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 28.

ОА АС ( как радиус, проведенный в точку касания )

- равнобедренный

0

( ОА=ОВ – как радиусы одной окружности )

28

А

В

С

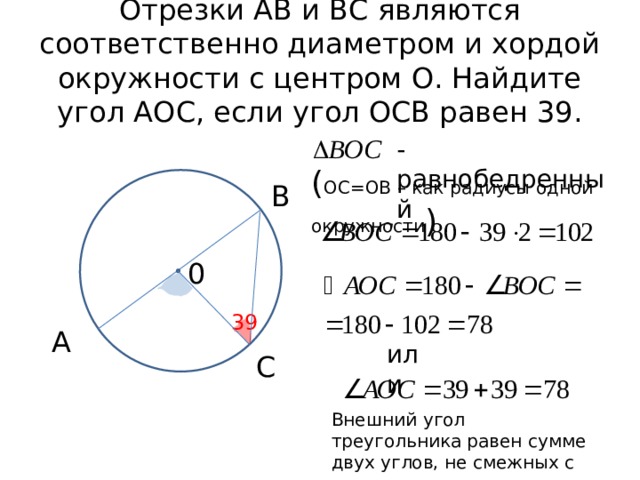
Отрезки АВ и ВС являются соответственно диаметром и хордой окружности с центром О. Найдите угол АОС, если угол ОСВ равен 39.

- равнобедренный

( ОС=ОВ – как радиусы одной окружности )

В

0

39

А

или

С

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

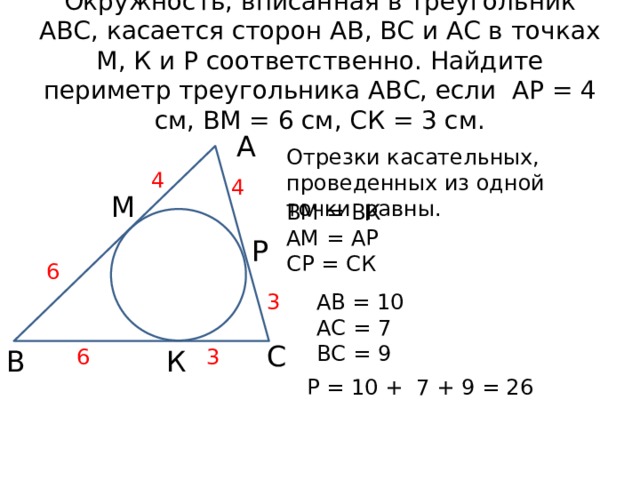
Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр треугольника АВС, если АР = 4 см, ВМ = 6 см, СК = 3 см.

А

Отрезки касательных, проведенных из одной точки равны.

4

4

М

ВМ = ВК

АМ = АР

СР = СК

Р

6

АВ = 10

3

АС = 7

ВС = 9

С

3

К

6

В

Р = 10 + 7 + 9 = 26

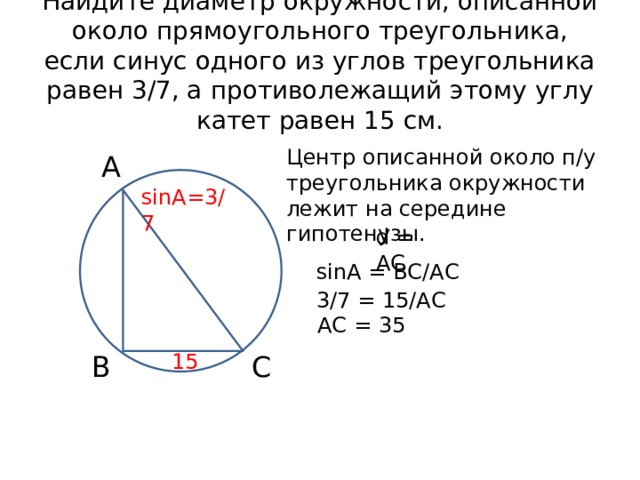
Найдите диаметр окружности, описанной около прямоугольного треугольника, если синус одного из углов треугольника равен 3/7, а противолежащий этому углу катет равен 15 см.

Центр описанной около п/у треугольника окружности лежит на середине гипотенузы.

А

sinA=3/7

d = AC

sinA = ВС/АС

3/7 = 15/АС

АС = 35

15

В

С

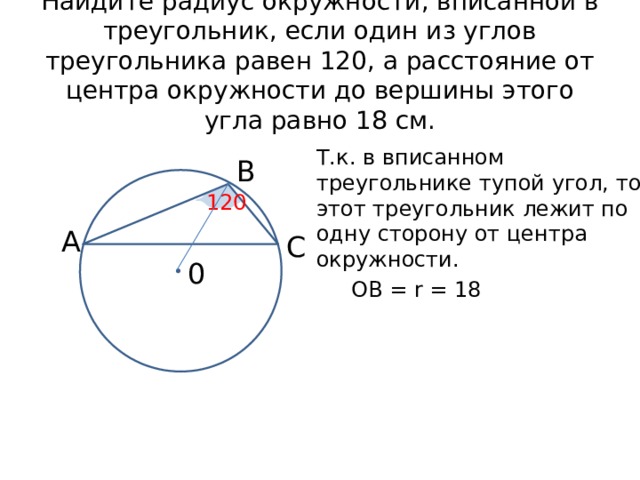
Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 120, а расстояние от центра окружности до вершины этого угла равно 18 см.

Т.к. в вписанном треугольнике тупой угол, то этот треугольник лежит по одну сторону от центра окружности.

В

120

А

С

0

ОВ = r = 18

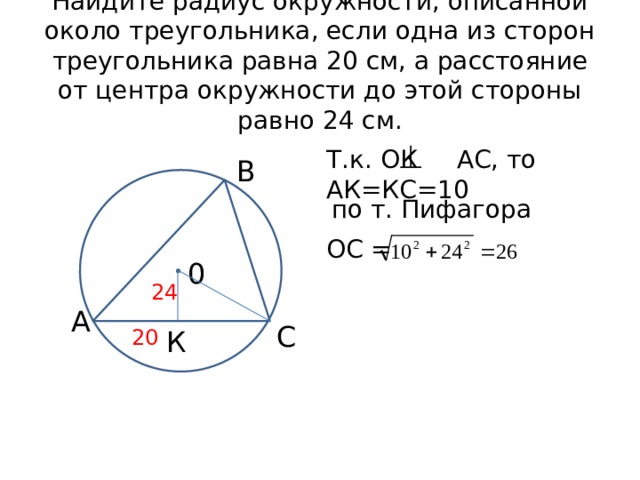
Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от центра окружности до этой стороны равно 24 см.

Т.к. ОК АС, то АК=КС=10

В

по т. Пифагора

ОС =

0

24

А

С

20

К

Уровень В

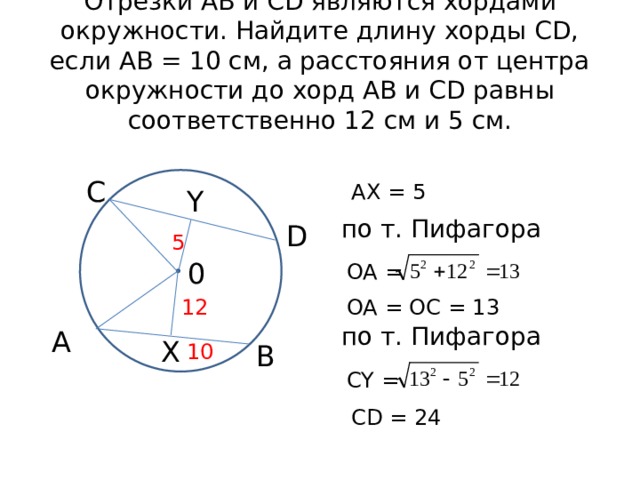
Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD, если АВ = 10 см, а расстояния от центра окружности до хорд АВ и CD равны соответственно 12 см и 5 см.

C

АХ = 5

Y

по т. Пифагора

D

5

0

ОА =

12

ОА = ОС = 13

по т. Пифагора

А

X

10

В

СY =

CD = 24

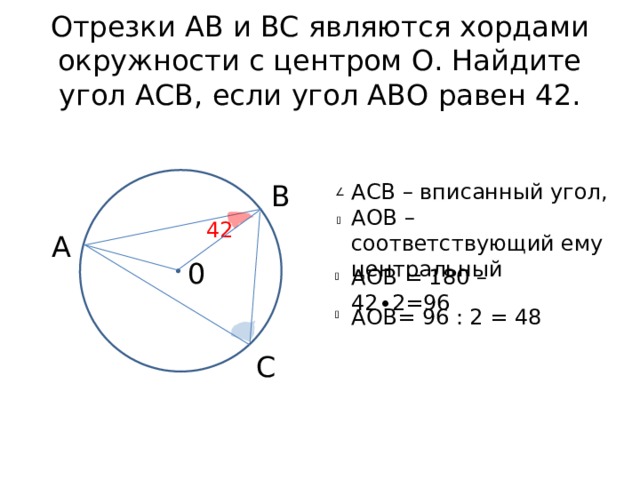
Отрезки АВ и BC являются хордами окружности с центром О. Найдите угол АСВ, если угол АВО равен 42.

В

АСВ – вписанный угол,

АОВ – соответствующий ему центральный

42

А

0

АОВ = 180 – 42∙2=96

АОВ= 96 : 2 = 48

С

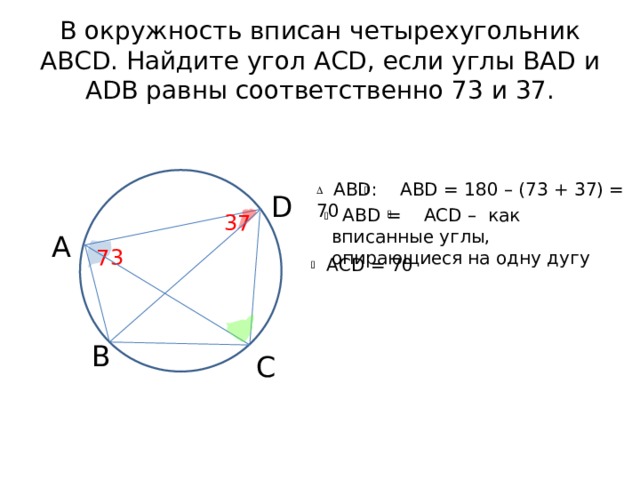
В окружность вписан четырехугольник АВСD. Найдите угол АСD, если углы BAD и ADB равны соответственно 73 и 37.

ABD: ABD = 180 – (73 + 37) = 70

D

АВD = ACD – как вписанные углы, опирающиеся на одну дугу

37

А

73

AСD = 70

В

С

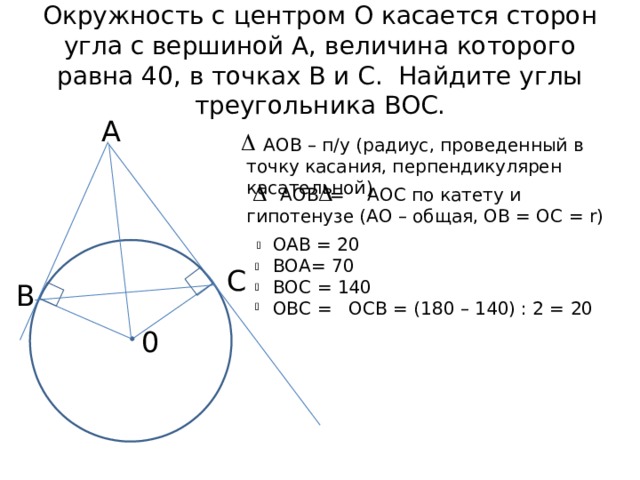
Окружность с центром О касается сторон угла с вершиной А, величина которого равна 40, в точках В и С. Найдите углы треугольника ВОС.

А

АОВ – п/у (радиус, проведенный в точку касания, перпендикулярен касательной)

АОВ = АОС по катету и гипотенузе (АО – общая, ОВ = ОС = r)

ОАВ = 20

ВОА= 70

ВОС = 140

ОВС = ОСВ = (180 – 140) : 2 = 20

С

В

0

Отрезки АВ и АС являются хордами окружности с центром О. Найдите угол ВАС, если известно, что он является острым и что углы АВО и АСО равны соответственно 23 и 32.

Угол ВАС – острый, значит его стороны лежат по разные стороны от центра окружности.

В

23

А

- равнобедренный

0

ОАВ = 23

- равнобедренный

32

ОАС = 32

ВАС = 23 + 32 = 55

С

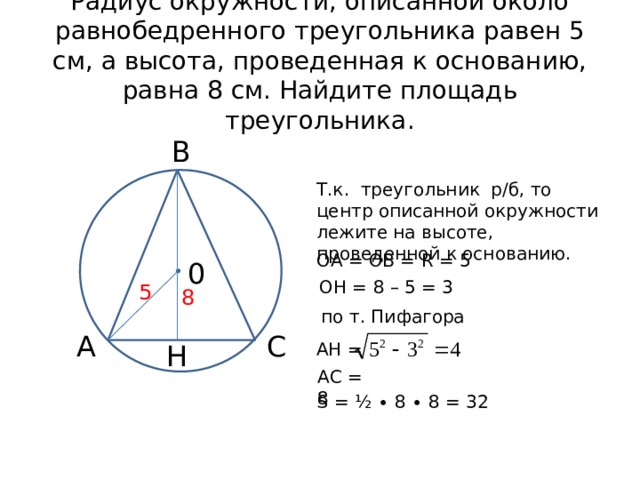
Радиус окружности, описанной около равнобедренного треугольника равен 5 см, а высота, проведенная к основанию, равна 8 см. Найдите площадь треугольника.

В

Т.к. треугольник р/б, то центр описанной окружности лежите на высоте, проведенной к основанию.

ОА = ОВ = R = 5

0

ОН = 8 – 5 = 3

5

8

по т. Пифагора

А

С

Н

АН =

АС = 8

S = ½ ∙ 8 ∙ 8 = 32

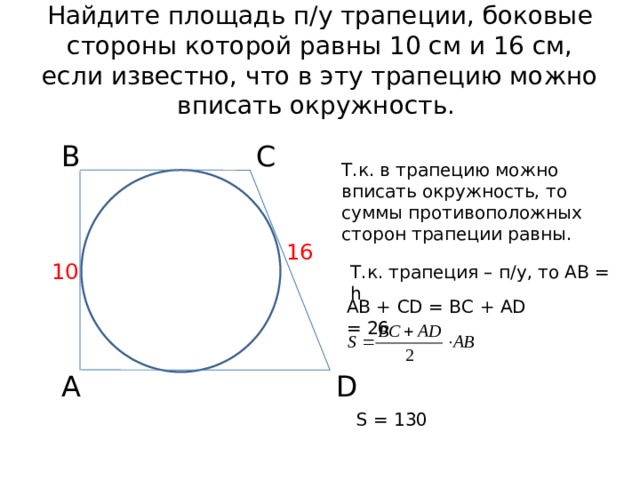
Найдите площадь п/у трапеции, боковые стороны которой равны 10 см и 16 см, если известно, что в эту трапецию можно вписать окружность.

В

С

Т.к. в трапецию можно вписать окружность, то суммы противоположных сторон трапеции равны.

16

10

Т.к. трапеция – п/у, то АВ = h

АВ + CD = ВС + AD = 26

А

D

S = 130

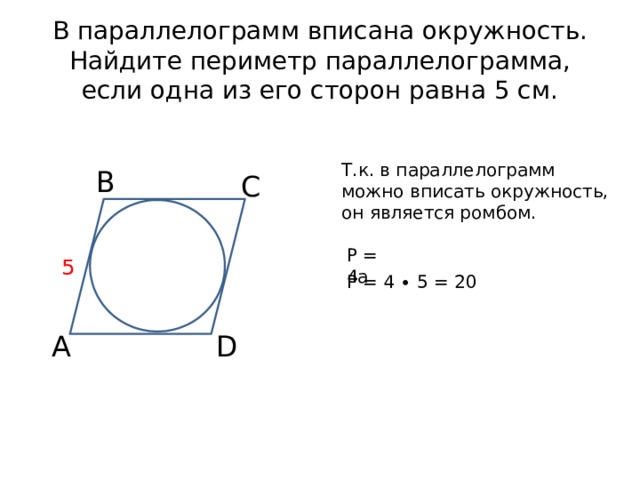
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5 см.

Т.к. в параллелограмм можно вписать окружность, он является ромбом.

В

С

Р = 4а

5

Р = 4 ∙ 5 = 20

А

D

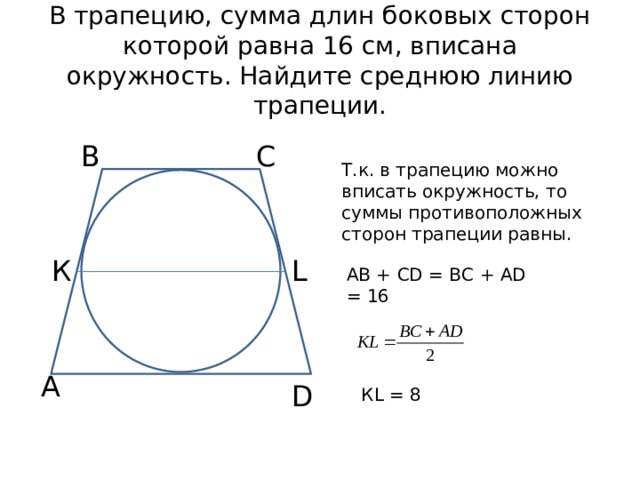
В трапецию, сумма длин боковых сторон которой равна 16 см, вписана окружность. Найдите среднюю линию трапеции.

В

С

Т.к. в трапецию можно вписать окружность, то суммы противоположных сторон трапеции равны.

К

L

АВ + CD = ВС + AD = 16

А

D

КL = 8