Всероссийская олимпиада школьников по физике (2014-2015 уч.г.)
Школьный этап, 7 класс
Решения
Задача 1. Ночью температура была -50С, а днем стала +120С. На сколько градусов изменилась температура воздуха? (5 баллов)
Ответ: температура увеличилась на 17 градусов.
Решение: изменение температуры +120С – (-50С) = 120С+50С = +170С.
Задача 2. Расположите в порядке возрастания: 0.02 м2, 5000мм2, 400см2, 0.7 дм2. (10 баллов)
Ответ: 5000 мм2; 0.7 дм2; 0.02 м2; 400 см2
Решение:
т.к. 1м = 10 дм = 100 см = 1000 мм,
то 1м2 = 102 дм2 = 104 см2 = 106 мм2,
поэтому: 0.02 м2 = 2∙10-2 м2 = 2∙100 дм2 = 2∙102 см2 = 2∙104 мм2
5000 мм2 = 5∙10-3 м2 = 5∙10-1 дм2 = 5∙101 см2 = 5∙103 мм2
400 см2 = 4∙10-2 м2 = 4∙100 дм2 = 4∙102 см2 = 4∙104 мм2
0.7 дм2 = 7∙10-3 м2 = 7∙10-1 дм2 = 7∙101 см2 = 7∙103 мм2
Сравнение необходимо проводить в одинаковых единицах измерения.
Задача 3.
Хочу я купить сапоги – скороходы,
Ходить в скороходах отлично в походы:
Шагнул один шаг – и проделал семь миль.
Обгонишь автобус, автомобиль…
За час не спеша обойдешь вокруг света,
Догнать тебя сможет только ракета!
Приняв 1 милю примерно за 1,6 км, длительность шага за 1с, а длину экватора за 40000км, рассчитайте, действительно ли можно обойти всю Землю за один час. (20 баллов)
Ответ: Можно.
Решение: Скорость движения семимильными шагами рассчитывается по длине шага 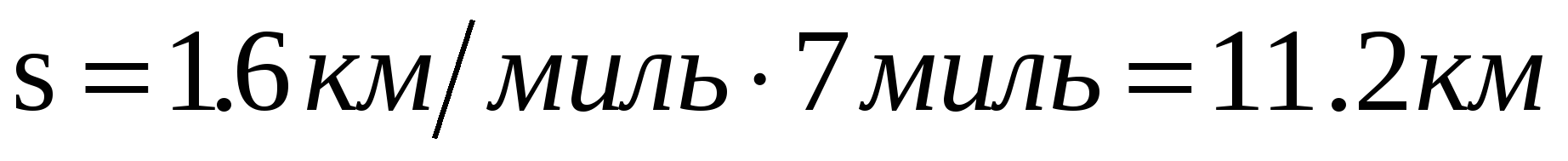 и времени его совершения
и времени его совершения 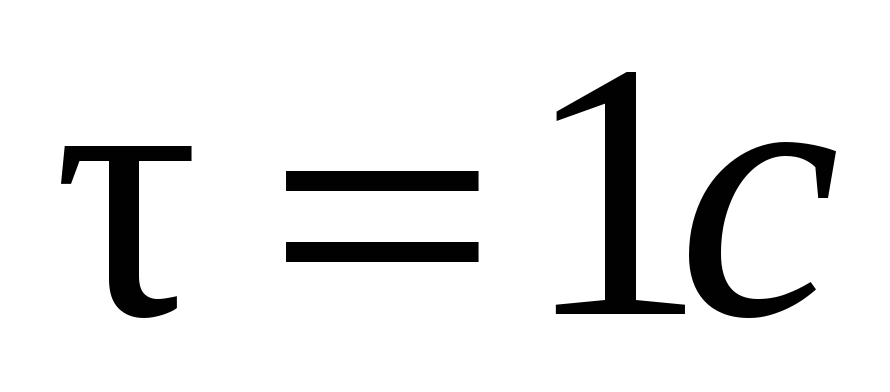 по формуле
по формуле  . Тогда время обхода экватора длиной
. Тогда время обхода экватора длиной  равно
равно  , что меньше чем 1час=3600с.
, что меньше чем 1час=3600с.
Задача 4. Длину ребра кубика увеличили в 3 раза. Во сколько раз изменились вследствие этого:
а) объем кубика;
б) площадь поверхности кубика;
в) суммарная длина всех ребер кубика?
(10 баллов)
Ответ: Увеличились а) в 27 раз; б) в 9 раз; в) в 3 раза.
Решение: Все линейные размеры кубика изменяются пропорционально 1-й степени длины его ребра. Все поверхностные размеры кубика изменяются пропорционально квадрату (2-й степени) длины его ребра. Все объемные размеры кубика изменяются пропорционально кубу (3-й степени) длины его ребра.
Задача 5. Если необходимо вынести из теплого помещения на холод музыкальные инструменты, то рекомендуют несколько уменьшить натяжение струн. Для чего это нужно сделать? (5 баллов)
Решение: При охлаждении струны становятся короче, их натяжение увеличивается. Это может привести к разрыву струн. Поэтому натяжение струн заранее уменьшают при выходе на холод.
Критерии оценки заданий:
| Приведено полное правильное решение, включающее следующие элементы: 1) Правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом. 2) выполнены (если необходимо для решения) рисунки и пояснения к ним. 3) проведены необходимые преобразования и расчёты, приводящие к правильному числовому ответу, и представлен ответ (для задач в общем виде приведена конечная формула), при этом допускается решение «по частям» (с промежуточными вычислениями). | 100% От количества баллов |
| Представлено правильное решение только в общем виде, без каких-либо числовых расчётов, (не относится к задачам в общем виде). Или правильно записаны необходимые формулы, записан правильный ответ, но не представлены преобразования, приводящие к ответу. | 70% |
| Правильно записаны необходимые формулы, но в математических преобразованиях или в вычислениях допущена ошибка, которая привела к неверному ответу. | 40% |
| Приведены формулы и размышления по теме задачи, но отсутствует решение. | 10% |
Всероссийская олимпиада школьников по физике (2014-2015 уч.г.)
Школьный этап, 8 класс
Решения
Задача 1. Колонна пехоты длиной L=400 м движется со скоростью u=4км/ч. Командир, находящийся во главе колонны, послал адъютанта с приказом к замыкающему. Через какое время адъютант вернется, если он едет на лошади со скоростью v=20км/ч? (10 баллов)
Ответ: 2,5 мин.
Решение:
Время движения против хода колонны  , время движения по ходу колонны
, время движения по ходу колонны 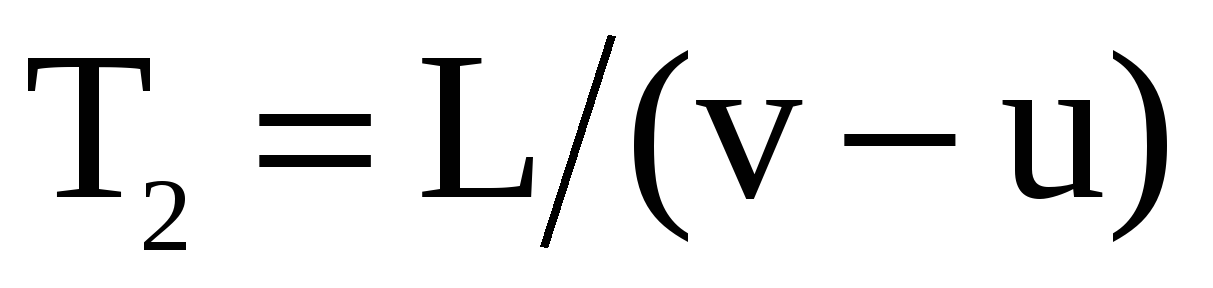 . Общее время движения
. Общее время движения 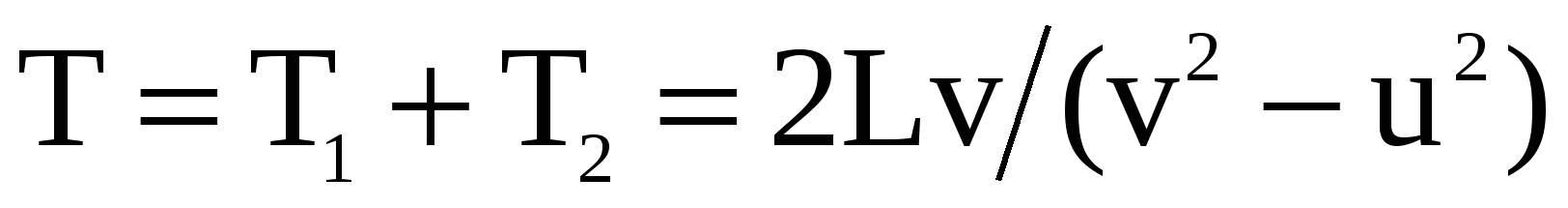 .
.
После подстановки численных данных получаем
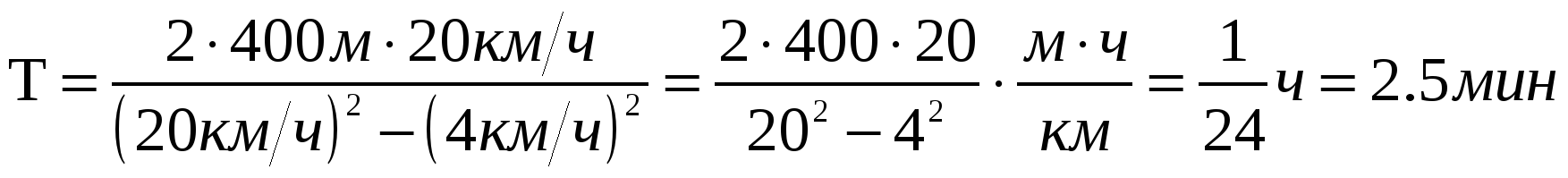
Задача 2. Масса каждого из двух одинаковых сосудов, заполненных свинцовой дробью, равна 2100 г. Когда в один из сосудов налили доверху воду, а в другой – неизвестную жидкость, массы сосудов стали соответственно 2200 г и 2185 г. Какова плотность неизвестной жидкости? (15 баллов)
Ответ: 850 кг/м3.
Решение: Массы воды и неизвестной жидкости в сосудах равны соответственно m1 = 2200г-2100г=100г и m2=2185г-2100г=85г. Т.к. сосуды одинаковы и вместе с дробью имеют одинаковые массы, то объемы V жидкостей в сосудах также одинаковы. Тогда по определению плотности 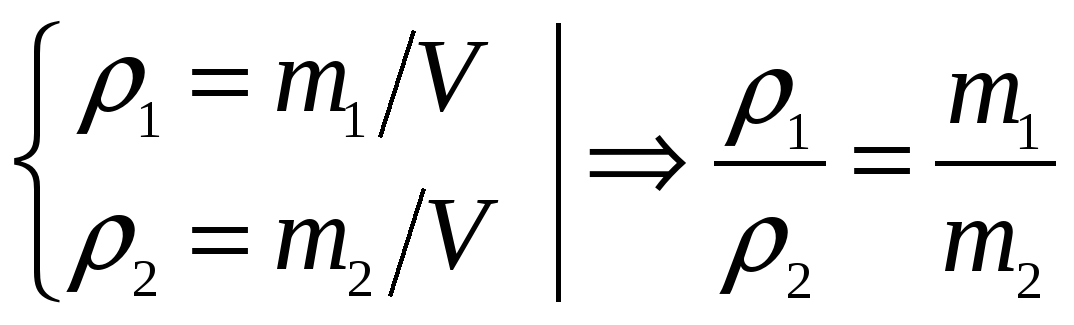 . Поэтому
. Поэтому 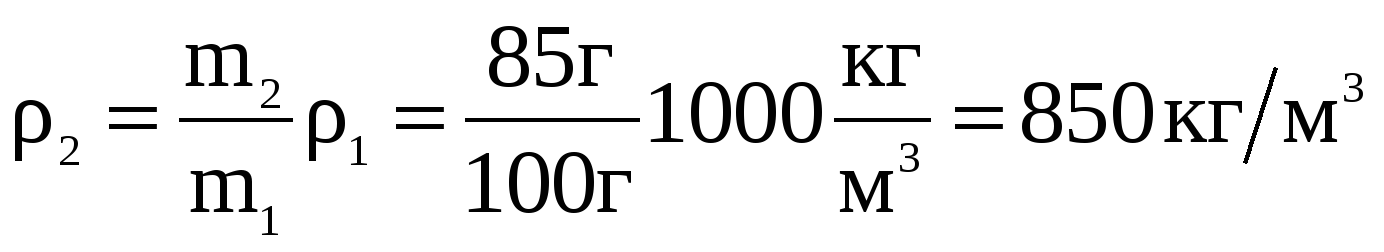
Задача 3. В мультфильме «Ну, погоди!» волк проглотил воздушный шарик и поднялся в воздух. Каким должен был стать объем волка, чтобы такое могло произойти? Считайте, что масса волка равна 30 кг. Плотность воздуха 1.29 кг/м3. (5 баллов)
Ответ: примерно 23.3м3.
Решение: Для того, чтобы такое могло произойти, средняя плотность волка (масса волка – m=30кг), проглотившего воздушный шарик, должна быть не больше плотности воздуха 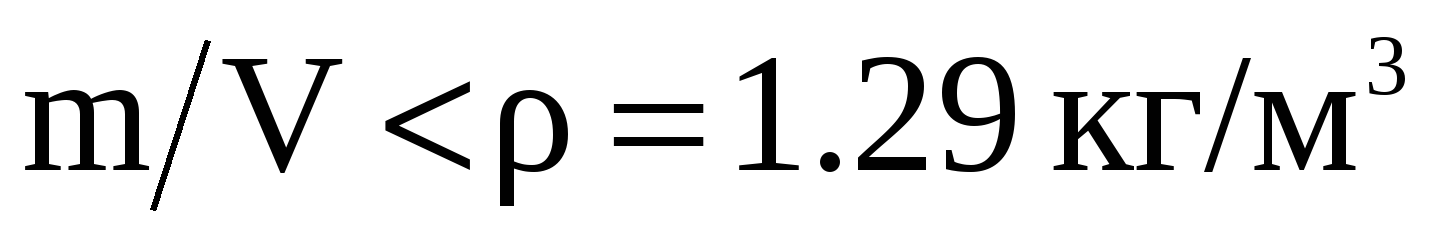 , что приводит к условию на объем волка
, что приводит к условию на объем волка  .
.
Задача 4. Прямолинейный кусок проволоки массой 40г подвешен за середину. Левую половину куска согнули пополам, как показано на рисунке. Какой массы груз надо подвесить в точке перегиба, чтобы восстановить равновесие? (20 баллов)
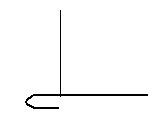
Ответ: 10г.
Решение: Пусть L – длина половины куска проволоки, M=40г – масса всего куска. На правую половину куска действует сила тяжести (M/2) ∙g с плечом L/2, создающая момент силы N1=(M/2) ∙g∙L/2=MgL/4. На левую, сложенную вдвое, половину куска действует сила тяжести (M/2) ∙g с плечом L/4, создающая момент силы N2=(M/2) ∙g∙L/4=MgL/8. На груз с левой стороны действует сила тяжести mg с плечом L/2, создающая момент силы N3=mgL/2.
Условие равновесия имеет вид N1=N2+N3, что приводит к уравнению для определения массы m груза: MgL/4= MgL/8+ mgL/2, решая которое получаем m=M/4=40г/4=10г.
Задача 5. Какой объем воды можно поднять из колодца глубиной 36 м за 1ч, если мощность электродвигателя насоса равна 5 кВт, а КПД установки 70%?
(10 баллов)
Ответ: 35м3.
Решение: Если из колодца глубиной h=36м будет поднят объем воды V, то при этом будет совершена полезная работа 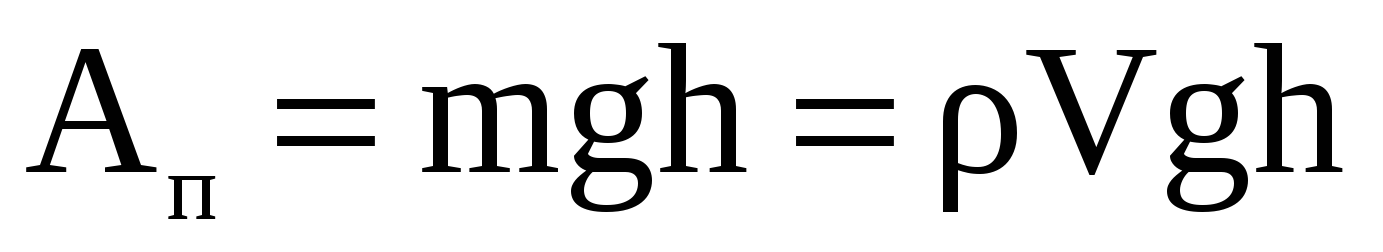 . При этом электродвигатель насоса мощностью P=5кВт за время подъема t=1ч совершит затраченную работу
. При этом электродвигатель насоса мощностью P=5кВт за время подъема t=1ч совершит затраченную работу 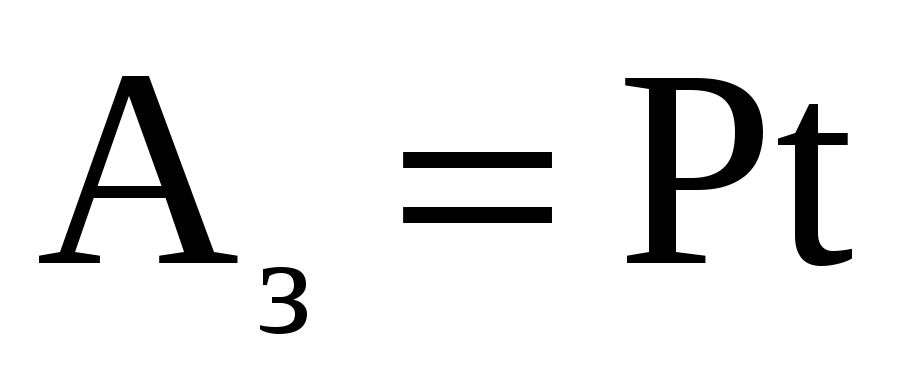 . По определению КПД установки
. По определению КПД установки  , поэтому
, поэтому 
Критерии оценки заданий:
| Приведено полное правильное решение, включающее следующие элементы: 1) Правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом. 2) выполнены (если необходимо для решения) рисунки и пояснения к ним. 3) проведены необходимые преобразования и расчёты, приводящие к правильному числовому ответу, и представлен ответ (для задач в общем виде приведена конечная формула), при этом допускается решение «по частям» (с промежуточными вычислениями). | 100% От количества баллов |
| Представлено правильное решение только в общем виде, без каких-либо числовых расчётов, (не относится к задачам в общем виде). Или правильно записаны необходимые формулы, записан правильный ответ, но не представлены преобразования, приводящие к ответу. | 70% |
| Правильно записаны необходимые формулы, но в математических преобразованиях или в вычислениях допущена ошибка, которая привела к неверному ответу. | 40% |
| Приведены формулы и размышления по теме задачи, но отсутствует решение. | 10% |
Всероссийская олимпиада школьников по физике (2014-2015 уч.г.)
Школьный этап, 9 класс
Решения
Задача 1. В калориметре при температуре 00С находятся вода массой 500 г и лед массой 300 г. Какая температура установится в калориметре, если долить в него 100 г кипятка? Удельная теплоемкость воды 4200 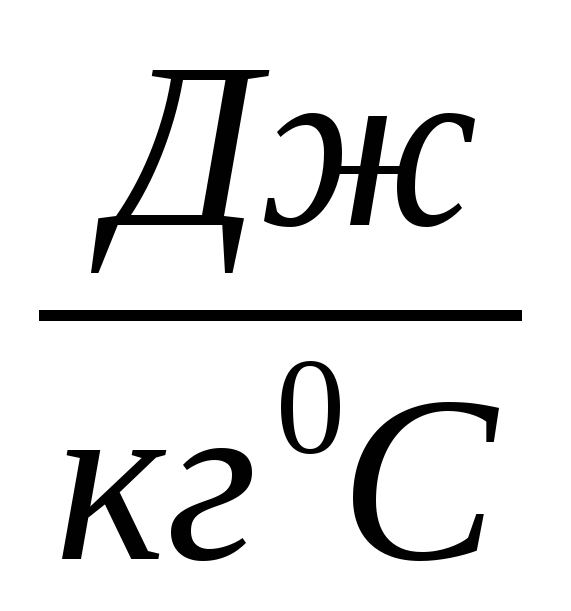 ; удельная теплота плавления льда 330кДж/кг. (10 баллов)
; удельная теплота плавления льда 330кДж/кг. (10 баллов)
Ответ: 00С.
Решение: Если температура в калориметре установится выше 00С, то находившийся в нем лед должен расплавиться, для чего требуется количество тепла  . Тепло для плавления льда может быть получено за счет остывания кипятка. Максимально возможное количество тепла кипяток отдаст при охлаждении до 00С (в этом случае расплавится не весь лед или весь лед расплавится, но дальнейшего повышения температуры сверх 00С не будет)
. Тепло для плавления льда может быть получено за счет остывания кипятка. Максимально возможное количество тепла кипяток отдаст при охлаждении до 00С (в этом случае расплавится не весь лед или весь лед расплавится, но дальнейшего повышения температуры сверх 00С не будет)  .
.
Т.к. 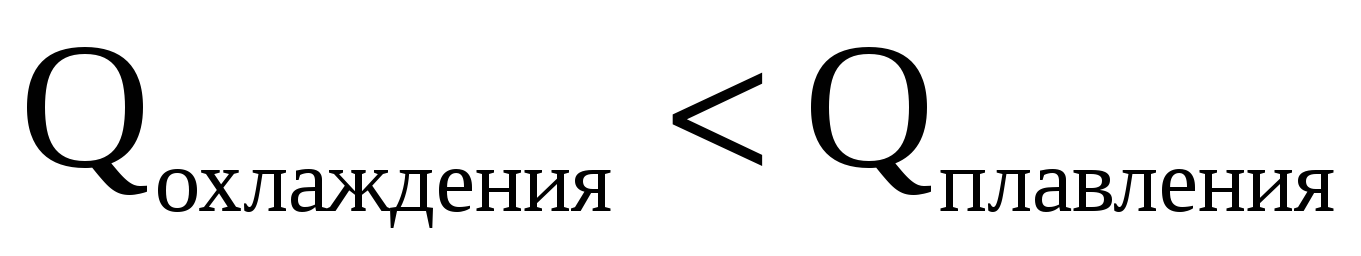 , то максимально возможной теплоты, выделяющейся при охлаждении кипятка, не достаточно, чтобы расплавить лед и температура останется 00С.
, то максимально возможной теплоты, выделяющейся при охлаждении кипятка, не достаточно, чтобы расплавить лед и температура останется 00С.
Задача 2.
Два зеркала взаимно перпендикулярны. Сколько изображений точки А дают эти зеркала? Постройте эти изображения.
A
(10 баллов)
Ответ: 3 изображения.
Решение: Вследствие отражения света от зеркала 1 возникает изображение А1, а вследствие отражения от зеркала 2 – изображение А2. Некоторые же лучи, отразившись сначала от зеркала 1, отражаются затем и от зеркала 2. После первого отражения пучок этих лучей как бы «Исходит» из точки А1 (в этой точке пересекаются продолжения лучей). Значит, после второго отражения появится еще мнимое изображение А3 точки А1 в зеркале 2. Изображение точки А2 в зеркале 1 тоже попадет в точку А3. Более двух отражений не испытывает ни один луч; следовательно, других изображений нет (точка А3 не может отразиться ни от одного из зеркал – для обоих зеркал она находится в «зазеркалье»).
А1 А

А3 А2
Задача 3. Чугунный шарик в воздухе весит 4,9 Н, а в воде – 3,9 Н. Сплошной этот шарик или полый? Если полый, то определите объем полости. Плотность чугуна 7000кг/м3, воды 1000кг/м3. (15 баллов)
Ответ: Имеется полость объемом 30см3.
Решение: Пусть 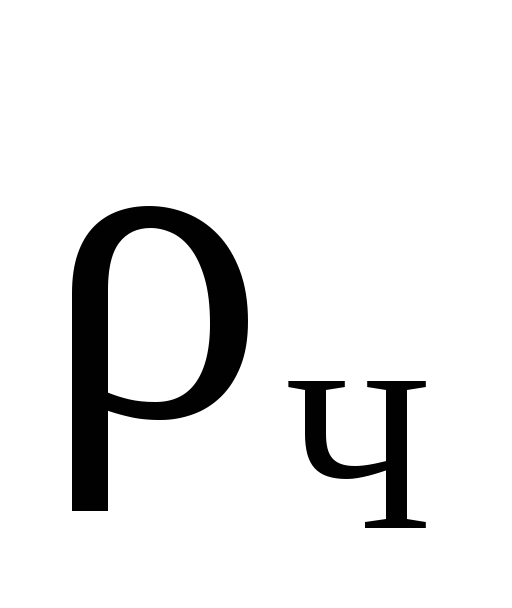 - плотность чугуна. Если пренебречь плотностью воздуха, то вес шарика в воздухе
- плотность чугуна. Если пренебречь плотностью воздуха, то вес шарика в воздухе 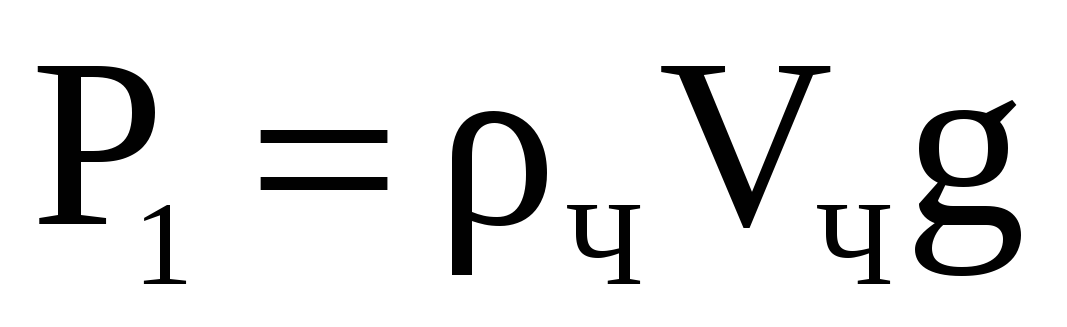 , что позволяет определить объем чугуна, из которого состоит шарик
, что позволяет определить объем чугуна, из которого состоит шарик 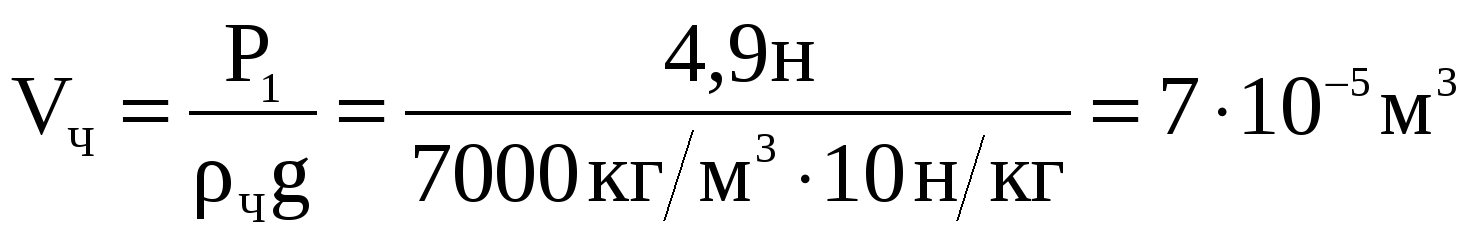 . Если поместить шарик в воду, то его вес уменьшится на величину выталкивающей силы Архимеда и станет равен
. Если поместить шарик в воду, то его вес уменьшится на величину выталкивающей силы Архимеда и станет равен 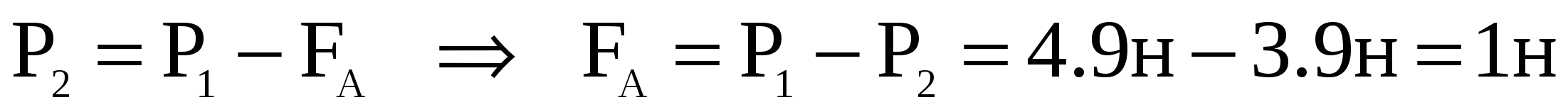 . С другой стороны, сила Архимеда зависит от объема шарика
. С другой стороны, сила Архимеда зависит от объема шарика  как геометрического тела (и следовательно, от наличия полости внутри чугунной оболочки и от ее объема
как геометрического тела (и следовательно, от наличия полости внутри чугунной оболочки и от ее объема  )
) 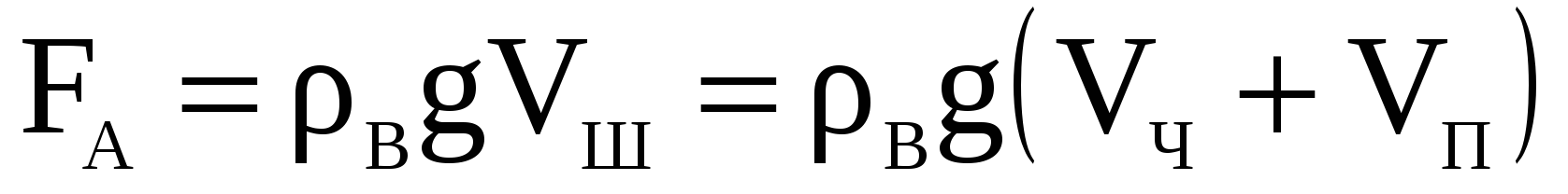 . Последнее уравнение позволяет определить объем полости:
. Последнее уравнение позволяет определить объем полости:
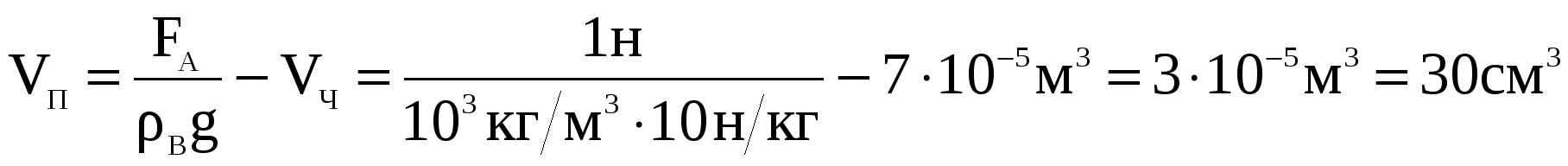
Задача 4. Ослик, пройдя по мосту 3/8 его длины, оглянувшись, увидел движущийся автомобиль. Если ослик повернет назад, то встретит автомобиль в начале моста, а если побежит вперед, то встретит автомобиль в конце моста. С какой скоростью бежал испуганный ослик, если скорость автомобиля υ? (10 баллов)
Ответ: скорость испуганного ослика u=v/4.
Решение: Пусть длина всего моста равна L,. а автомобиль, когда его увидел ослик, находился от моста на расстоянии S. Если ослик со скоростью u побежал назад, то времена движения автомобиля и ослика до начала моста равны по условию  . Аналогично, времена движения автомобиля и ослика до конца моста равны по условию, если ослик со скоростью u побежал вперед
. Аналогично, времена движения автомобиля и ослика до конца моста равны по условию, если ослик со скоростью u побежал вперед 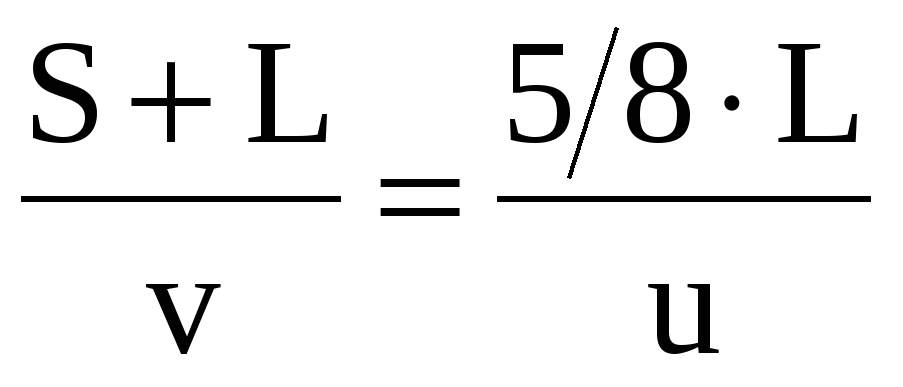 . Почленным делением уравнений друг на друга получаем
. Почленным делением уравнений друг на друга получаем 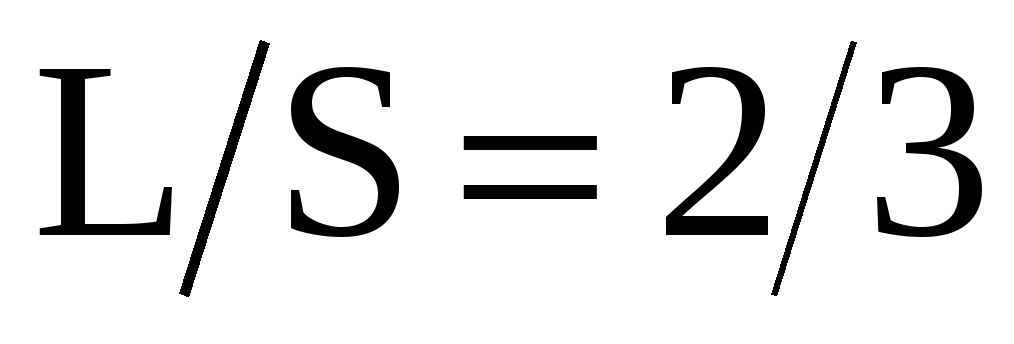 , что после подстановки в любое из исходных уравнений позволяет определить скорость ослика
, что после подстановки в любое из исходных уравнений позволяет определить скорость ослика 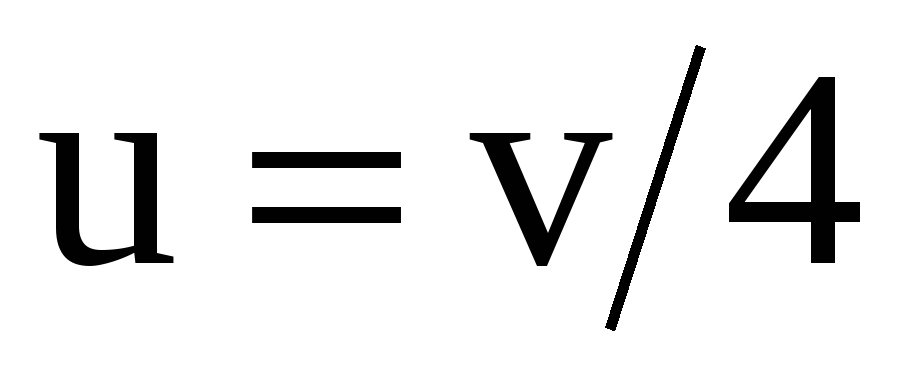 .
.
Задача 5. Предложите способ определения диаметра небольшого шарика, если в Вашем распоряжении имеется мензурка с водой и неограниченное количество одинаковых шариков. (5 баллов)
Решение: Сначала насыпаем в мензурку с водой достаточное количество N маленьких шариков так, чтобы изменение уровня воды в мензурке существенно превышало цену деления мензурки (необходимо для повышения точности измерения объема шариков). По изменению уровня воды в мензурке обычным образом определяем суммарный объем VN всех шариков и рассчитываем объем V= VN/N одного шарика. Диаметр d каждого из шариков находится при помощи формулы объема шара  .
.
Критерии оценки заданий:
| Приведено полное правильное решение, включающее следующие элементы: 1) Правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом. 2) выполнены (если необходимо для решения) рисунки и пояснения к ним. 3) проведены необходимые преобразования и расчёты, приводящие к правильному числовому ответу, и представлен ответ (для задач в общем виде приведена конечная формула), при этом допускается решение «по частям» (с промежуточными вычислениями). | 100% От количества баллов |
| Представлено правильное решение только в общем виде, без каких-либо числовых расчётов, (не относится к задачам в общем виде). Или правильно записаны необходимые формулы, записан правильный ответ, но не представлены преобразования, приводящие к ответу. | 70% |
| Правильно записаны необходимые формулы, но в математических преобразованиях или в вычислениях допущена ошибка, которая привела к неверному ответу. | 40% |
| Приведены формулы и размышления по теме задачи, но отсутствует решение. | 10% |
Всероссийская олимпиада школьников по физике (2014-2015 уч.г.)
Школьный этап, 10 класс
Решения
Задача 1. Два шара одинакового объема, но разной массы: 5кг и 2кг соединены нитью. Определите силу натяжения нити, соединяющей шары, если они плавают в вертикальном положении, полностью погрузившись в воду. (10 баллов)
Ответ: T=15н.
Решение: Очевидно, что более тяжелый шар с массой m1=5кг будет расположен ниже шара с массой m2=3кг. На каждый из шаров действуют различные по величине силы тяжести, одинаковые по величине FА и направлению архимедовы силы и одинаковые по величине T, но противоположные по направлению силы натяжения нити. Условия равновесия шаров в проекции на вертикально вниз направленную ось имеют вид:
m2g-FА-T=0
m1g-FА+T=0
После исключения FА из системы уравнений получаем
T=( m1- m2)g/2=(5кг-2кг)(10н/кг)/2=15н
Задача 2. Как изменилась бы продолжительность земного года, если бы масса Земли стала равной массе Солнца, а расстояние между ними осталось тем же? (15 баллов)
Ответ: Увеличилась в  раз.
раз.
Решение: Уравнения динамики вращательного движения Земли под действием силы гравитационного притяжения к Солнцу в двух предложенных ситуациях имеют вид:

Здесь: 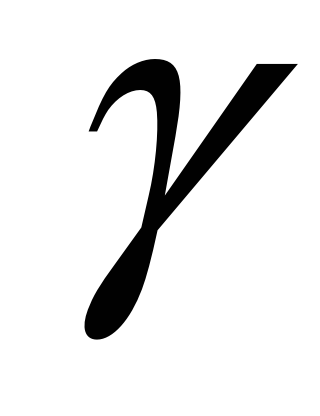 - гравитационная постоянная,
- гравитационная постоянная, 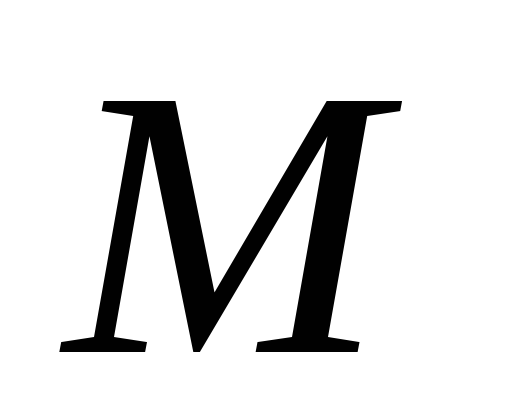 - масса Солнца,
- масса Солнца,  - истинная масса Земли,
- истинная масса Земли, 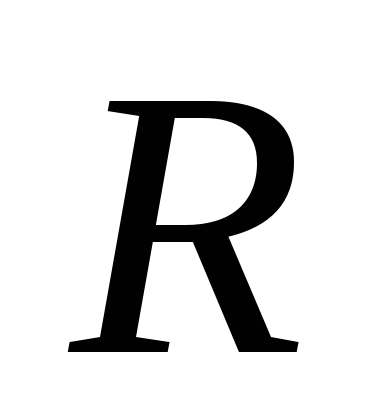 - расстояние между Солнцем и Землей,
- расстояние между Солнцем и Землей,  - угловая скорость движения Земли по орбите. Заметим, что в 1-й ситуации
- угловая скорость движения Земли по орбите. Заметим, что в 1-й ситуации 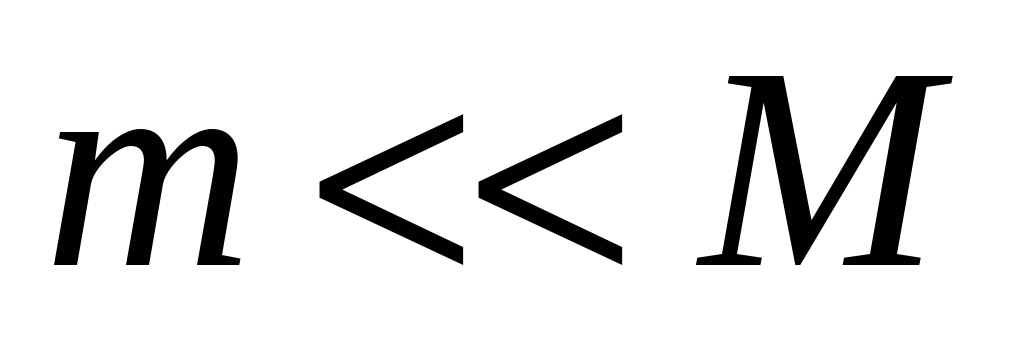 и Солнце является центром орбиты Земли. Во 2-й ситуации
и Солнце является центром орбиты Земли. Во 2-й ситуации 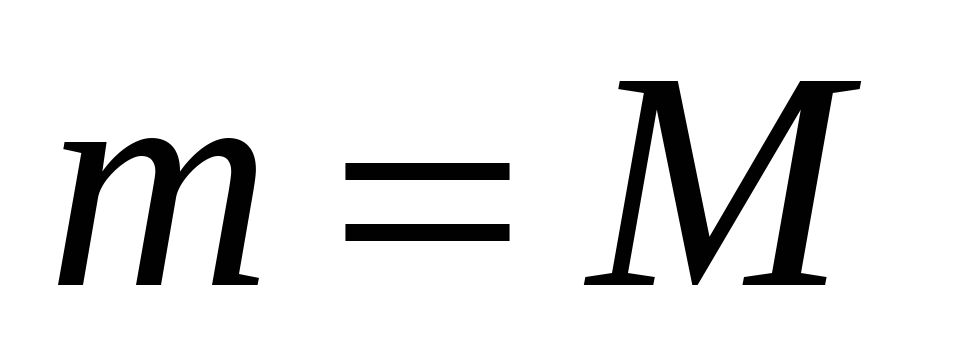 и центр орбиты Земли лежит по середине между Солнцем и Землей, в результате чего радиус орбиты уменьшается в 2 раза. Делением уравнений друг на друга получаем:
и центр орбиты Земли лежит по середине между Солнцем и Землей, в результате чего радиус орбиты уменьшается в 2 раза. Делением уравнений друг на друга получаем: 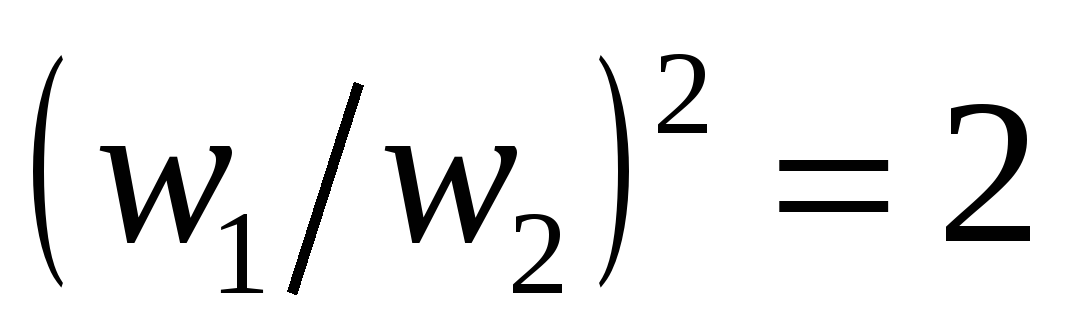 . Поэтому отношение периодов обращения
. Поэтому отношение периодов обращения  .
.
Задача 3. Пять электрических лампочек рассчитаны на 110В каждая. Три из них имеют мощность по 40 Вт, а две - по 60 Вт. Как следует включить их в сеть с напряжением 220 В, чтобы все горели нормальным накалом? (15 баллов).
Ответ: 40Вт
Включать надо так:

60Втт




























60Вт
40Вт
40Вт




Решение: Т.к. выделяющаяся на лампочке мощность равна P=U2/R, то по номинальной мощности P и рабочему напряжению U определяется сопротивление лампы R=U2/P. Т.к. рабочие напряжения всех пяти ламп одинаковы, то сопротивления ламп обратно пропорциональны их номинальным мощностям R60/R40=P40/P60=2/3. Для того, чтобы 220В напряжения питания распределить поровну на рабочие напряжения по 110В необходимо иметь две последовательно включенные группы ламп, причем сопротивления групп должны быть одинаковы. Для того, чтобы лампы горели нормальным накалом, внутри каждой группы лампы должны быть включены параллельно, т.к. при этом каждая из ламп группы будет находиться под рабочим напряжением 110В. Для сопротивления группы параллельно включенных ламп (i-номер лампы) под напряжением U имеем 1/R=∑1/Ri=∑1/(U2/Pi)= ∑Pi/ U2. Т.о. для того, чтобы сопротивления групп были одинаковыми, необходимо, чтобы были одинаковы суммы номинальных мощностей ламп в группах.
Задача 4. Теплый воздух, как известно, поднимается вверх. Почему же на высоте 10 км постоянно держится температура -500С? (5 баллов)
Решение: Давление воздуха уменьшается с высотой. Поэтому при подъеме воздух расширяется. При расширении он совершает работу, расходуя на это часть своей внутренней энергии. Это и является главной причиной охлаждения воздуха.
Задача 5. Предложите способ при помощи линейки без делений и карандаша определить положение центра тяжести однородной Г-образной пластинки, все углы которой прямые. (5 баллов)
Решение: Разобьем мысленно пластинку на два прямоугольника. Как показано пунктиром на рис. а) и б), это можно сделать двумя способами. Центр тяжести каждого прямоугольника будет лежать в точке пересечения его диагоналей. В каждом из вариантов разбиения центр тяжести всей пластины должен лежать на прямой линии, соединяющей центры тяжести составляющих пластину прямоугольников. Но если центр тяжести пластины находится одновременно на двух прямых A1A2 и B1B2, то он должен совпасть с точкой их пересечения (рис. в).
Критерии оценки заданий:
| Приведено полное правильное решение, включающее следующие элементы: 1) Правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом. 2) выполнены (если необходимо для решения) рисунки и пояснения к ним. 3) проведены необходимые преобразования и расчёты, приводящие к правильному числовому ответу, и представлен ответ (для задач в общем виде приведена конечная формула), при этом допускается решение «по частям» (с промежуточными вычислениями). | 100% От количества баллов |
| Представлено правильное решение только в общем виде, без каких-либо числовых расчётов, (не относится к задачам в общем виде). Или правильно записаны необходимые формулы, записан правильный ответ, но не представлены преобразования, приводящие к ответу. | 70% |
| Правильно записаны необходимые формулы, но в математических преобразованиях или в вычислениях допущена ошибка, которая привела к неверному ответу. | 40% |
| Приведены формулы и размышления по теме задачи, но отсутствует решение. | 10% |
Всероссийская олимпиада школьников по физике (2014-2015 уч.г.)
Школьный этап, 11 класс
Решения
Задача 1. Гвоздь забили в доску пятью ударами молотка массой 1кг. Скорость молотка перед ударом была 2м/с. Найдите длину гвоздя, если для начала его удаления из доски потребовалось приложить силу, равную 200Н. (15 баллов)
Ответ: 10см.
Решение: Процесс забивания гвоздя при каждом из ударов можно рассматривать как состоящий из двух этапов. На первом этапе происходит мгновенный (по сравнению с длительностью второго этапа) абсолютно неупругий удар молотка по гвоздю, в результате которого система гвоздь+молоток (СГМ) сразу после удара приобретает единую скорость. T.к. удар происходит мгновенно, то импульсом всех внешних сил (трение гвоздя о доску и воздействие руки человека на молоток) на первом этапе можно пренебречь, что означает выполнение на первом этапе закона сохранения импульса для СГМ. Т.к. масса гвоздя гораздо меньше массы молотка m=1кг, то в результате сохранения импульса скорость СГМ сразу после удара равна скорости v=2м/с молотка до удара, масса СГМ при этом равна массе молотка. Т.о., вследствие мгновенности удара и малости массы гвоздя, молоток при ударе не изменяет скорости, а гвоздь мгновенно разгоняется до скорости молотка v. На втором этапе каждого удара происходит движение гвоздя вглубь доски и торможение СГМ посредством трения гвоздя о доску.
За n=5 ударов вся кинетическая энергия Eк=nmv2/2, сообщенная молотку, будет израсходована на работу по преодолению трения гвоздя о доску. Величина силы трения f прямо пропорциональна длине l забитой части гвоздя, поэтому сила трения f(l) линейно возрастает от ноля до своего максимального значения F=200Н при изменении l от ноля до длины гвоздя L. Работа силы трения может быть найдена как площадь треугольника под графиком зависимости f(l) при 0lL, что дает Aтр=FL/2.
Тогда по закону сохранения энергии:
Задача 2. Холодильник потребляет от сети 400 Вт. При этом его излучение тепла в комнату составляет 450 Вт. За какое время в нем можно заморозить двухлитровый баллон с водой при начальной температуре 20оС? Удельная теплоемкость воды - 4200Дж/кг.оС, плотность воды - 1000кг/м3, удельная теплота плавления льда – 3,3.105Дж/кг. (5 баллов)
Ответ: t=4.6 ч.
Решение: По отношению к окружающей среде холодильник работает как обычный нагреватель, потребляя электрическую энергию от сети и выделяя ее в виде тепла во внешнюю среду. Однако при этом он передает во внешнюю среду еще и тепло, отнятое от продуктов. Это означает, что полезная (отобранная от продуктов) тепловая мощность равна P=450Вт-400Вт=50Вт. Вся полезная тепловая мощность идет на охлаждение и заморозку баллона с водой P.t=cm∆T+mλ. Поэтому:
Задача 3. Ребра проволочного тетраэдра ABCD имеют одинаковое сопротивление . Определите сопротивление 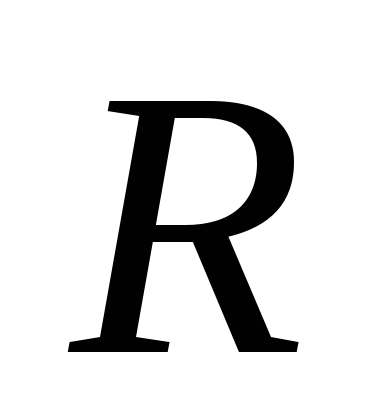 между точками A и B тетраэдра. (10 баллов)
между точками A и B тетраэдра. (10 баллов)
Ответ: r/2.
Решение: Вследствие симметрии ток между точками C и D тетраэдра не течет. Поэтому сопротивление тетраэдра может быть рассчитано, как сопротивление трех параллельно включенных участков AB, ACB, и ADB. Первый из них имеет сопротивление , а оставшиеся два по . Поэтому:
.
Задача 4. Электрическая лампочка объемом V=0.5л наполнена идеальным одноатомным газом до давления P0=2кПа. Лампочку теплоизолировали и подключили к сети постоянного тока напряжением U=12В. Определите давление P газа в лампочке после пропускания тока I=0.5А в течение секунд. (15 баллов)
Ответ: P=82кПа
Решение: Количество тепла, выделяемое спиралью лампочки при пропускании тока . Это тепло пошло на увеличение внутренней энергии молей газа в лампочке и привело к повышению температуры газа на . Объем и количество газа в лампочке не изменяются, поэтому из уравнения Менделеева-Клапейрона следует связь изменений давления и температуры . Тогда для изменения давления имеем:
Конечное давление .
Задача 5. Предложите способ при помощи линейки без делений и карандаша определить положение центра тяжести однородной Г-образной пластинки, все углы которой прямые. (5 баллов)
Решение: Разобьем мысленно пластинку на два прямоугольника. Как показано пунктиром на рис. а) и б), это можно сделать двумя способами. Центр тяжести каждого прямоугольника будет лежать в точке пересечения его диагоналей. В каждом из вариантов разбиения центр тяжести всей пластины должен лежать на прямой линии, соединяющей центры тяжести составляющих пластину прямоугольников. Но если центр тяжести пластины находится одновременно на двух прямых A1A2 и B1B2, то он должен совпасть с точкой их пересечения (рис. в).
Критерии оценки заданий:
| Приведено полное правильное решение, включающее следующие элементы: 1) Правильно записаны формулы, выражающие закономерности, применение которых необходимо для решения задачи выбранным способом. 2) выполнены (если необходимо для решения) рисунки и пояснения к ним. 3) проведены необходимые преобразования и расчёты, приводящие к правильному числовому ответу, и представлен ответ (для задач в общем виде приведена конечная формула), при этом допускается решение «по частям» (с промежуточными вычислениями). | 100% От количества баллов |
| Представлено правильное решение только в общем виде, без каких-либо числовых расчётов, (не относится к задачам в общем виде). Или правильно записаны необходимые формулы, записан правильный ответ, но не представлены преобразования, приводящие к ответу. | 70% |
| Правильно записаны необходимые формулы, но в математических преобразованиях или в вычислениях допущена ошибка, которая привела к неверному ответу. | 40% |
| Приведены формулы и размышления по теме задачи, но отсутствует решение. | 10% |







 некоторых странах, например, США и Канаде измерение температуры производится не по шкале Цельсия, а по шкале Фаренгейта. На рисунке показан такой термометр. Определите цену деления шкалы Цельсия и шкалы Фаренгейта и определите значения температуры.
некоторых странах, например, США и Канаде измерение температуры производится не по шкале Цельсия, а по шкале Фаренгейта. На рисунке показан такой термометр. Определите цену деления шкалы Цельсия и шкалы Фаренгейта и определите значения температуры. 
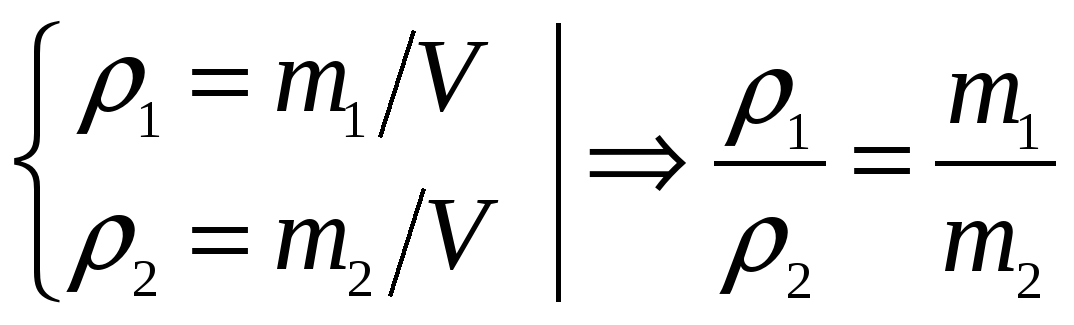 . Поэтому
. Поэтому 


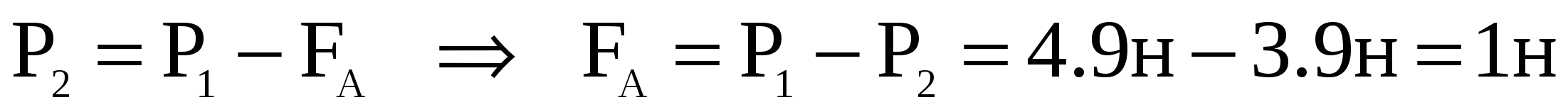 . С другой стороны, сила Архимеда зависит от объема шарика
. С другой стороны, сила Архимеда зависит от объема шарика  .
.












