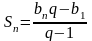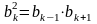Открытый урок алгебры в 9 классе.
Тема урока: «Арифметическая и геометрическая прогрессии»
Цель урока: обобщить, систематизировать и расширить знания, закрепить умения и навыки учащихся при решении задач по теме «Арифметическая и геометрическая прогрессии».
Задачи урока:
-
Обучающая – применение знаний к решению нестандартных задач, расширение кругозора по истории темы, использование знаний по теме в повседневной жизни; проверить полноту и осознанность усвоения знаний учащихся по теме.
-
Развивающая – формирование логического мышления, умения анализировать, сопоставлять и обобщать полученные знания.
-
Воспитательная – показать важность полученных знаний в жизни.
Тип урока: урок комплексного применения знаний (урок-практикум).
Формы работы:
-
фронтальная;
-
индивидуальная;
-
работа в парах.
Оборудование: презентация, мультимедийный проектор, экран; компьютеры, раздаточный материал.
Используемые педагогические технологии:
-
технология обучения математики на основе решения задач;
-
технология уровневой дифференциации;
-
технология проблемного обучения;
-
игровые технологии;
-
компьютерные технологии.
Ход урока.
-
Организационный момент.
Нам, людям, свойственно искать
Закономерности в явлениях, нас окружающих.
И миру чисел исключением не стать:
Прогрессии – движенье мысли в умах рождающие,
Закономерности, которые нам надо постигать.
Сегодня на уроке лозунг нас зовёт:
«Прогрессио – движение вперёд!».
Мы начинаем наш урок.
Ваши глубокие познания прогрессии
Должны всех нас сегодня удивить.
Все устные задания
Вам нужно на одном дыхании решить.
Ведь формулы и определения известны нам теперь.
И в мир задач решения нам широко открыта дверь.
-
Систематизация знаний.
Сегодня на уроке мы будем решать практические задачи на арифметическую и геометрическую прогрессии. Но, прежде чем мы приступим к их решению, необходимо вспомнить теоретический материал, на котором базируется решение задач.
Фронтальная работа с классом:
-
Дать определение арифметической и геометрической прогрессий.
-
Что называется разностью арифметической прогрессии?
-
Что называется знаменателем геометрической прогрессии?
-
Какая последовательность называется возрастающей?
-
Какая последовательность называется убывающей?
-
Задание: Среди каждой группы формул выбрать верную (Слайды ).
-
Решите устно задачи (слайды ).
№1. Дано: (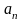 ) – арифметическая прогрессия,
) – арифметическая прогрессия, 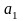 =-2,
=-2, 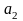 = 4.
= 4.
Найти: d- ?,  - ?
- ?
№2. Дано: ( ) – геометрическая прогрессия,
) – геометрическая прогрессия,  =2,
=2, 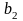 = 1.
= 1.
Найти: q- ?, 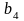 - ?
- ?
№3. Дано: (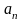 ) – арифметическая прогрессия,
) – арифметическая прогрессия, 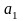 =-2,
=-2, 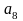 = 14.
= 14.
Найти:  - ?
- ?
№4. Дано: ( ) – геометрическая прогрессия,
) – геометрическая прогрессия,  =1,
=1, 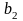 = 2.
= 2.
Найти: 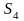 - ?
- ?
-
Определите вид прогрессии, соответствующий условию данной задачи. Объясните свой ответ.
-
Игорь начал утренние тренировки в беге с 2 км в день. Он решил каждую неделю увеличивать дистанцию на одно и то же расстояние, так чтобы в одиннадцатую неделю пробегать 4 км в день. Найдите это расстояние.
Ответ: Арифметическая прогрессия, так как дистанция увеличивается на одно и то же расстояние.
-
Завод приобрел 5 электромоторов, мощности которых отличаются в одно и то же число раз. Рассчитать мощности трех средних моторов, если известно, что наименьшая мощность мотора 5 кВт, а наибольшая 13,72 кВт.
Ответ: Геометрическая прогрессия, так как мощности моторов отличаются в одно и то же число раз.
-
Каждый курильщик выкуривает в день в среднем 8 сигарет. После выкуривания первой сигареты в легких оседает 0,2 мг никотина и табачного дегтя. С каждой последующей сигаретой это количество увеличивается на 0,001 мг. Какое количество вредных веществ оседает в легких за неделю?
Ответ: Арифметическая прогрессия, так как количество вредных веществ увеличивается на одно и то же число.
-
Самостоятельная работа.
I уровень – математический диктант (с последующей проверкой).
II уровень – самостоятельная работа (с последующей взаимопроверкой).
III уровень – компьютерное тестирование.
I уровень. Математический диктант.
Учащимся раздаются карточки с формулами и некоторыми равенствами, лист для введения ответов на вопросы диктанта.
| 1 | 2 | 3 | 4 | 5 |
| 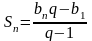 | 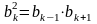 | an =a1 + d(n – 1) | S5 = 11 |  |
| 6 | 7 | 8 | 9 | 10 |
| 2; 4; 8; 16; 32; …; |  |  | 1; 4; 7; 10; 13; …; | S5 = 0 |

Лист ответа:
Выполнил: ___________________________
Количество правильных ответов: ________
Оценка: ______
Учитель:
-
Формула суммы n первых членов арифметической прогрессии.
-
Характеристическое свойство арифметической прогрессии
-
Первый член арифметической прогрессии равен 6, пятый член равен - 6. Найти сумму первых пяти членов.
-
Формула n-го члена геометрической прогрессии.
-
Характеристическое свойство геометрической прогрессии.
-
Первый член геометрической прогрессии равен 1, знаменатель равен -2. Найти сумму первых пяти членов.
-
Пример арифметической прогрессии.
-
Формула суммы n членов геометрической прогрессии.
-
Пример геометрической прогрессии.
-
Формула n-го члена арифметической прогрессии.
Проверка выполнения работы
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 8 | 10 | 7 | 2 | 4 | 9 | 1 | 6 | 3 |
Критерии оценок:
«5» - 10 правильных ответов
«4» - 8-9 правильных ответов
«3» - 5-7 правильных ответов
«2» - менее 5 правильных ответов
II уровень. Самостоятельная работа (в двух вариантах).
| Вариант 1. Дана арифметическая прогрессия: -
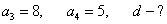 -
 -
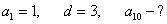 -
 Дана геометрическая прогрессия: -
 -
 -
-

| Вариант 2. Дана арифметическая прогрессия: -
 -
 -
 -
 Дана геометрическая прогрессия: -
 -
 -
-

|
Взаимопроверка:
«5» - 8 баллов;
«4» - 6 – 7 баллов;
«3» - 4 – 5 баллов;
«2» - меньше 4 баллов.
III уровень. Компьютерное тестирование (оценки выставляет компьютер).
-
Игровая разминка.
На экране записано 20 чисел:
1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40. 43, 46, 49, 52, 55, 58.
Учитель стоит спиной к экрану. Ученики называют номер числа, а учитель мгновенно называет само число. Потом он предлагает учащимся объяснить, как ему это удаётся. (Учитель помнит формулу n-го члена а=3n -2).
-
Решение задач.
Представьте, что вы располагаете некоторой суммой и хотите положить ее в банк на три года на вклад, по которому начисляется 10% годовых. У вас есть возможность ежегодно получать проценты по вкладу. Как в этом случае будет расти ваш доход?
Ответ: Доход будет расти в арифметической прогрессии, так как ежегодно сумма дохода будет увеличиваться на одну и ту же сумму (10% от вклада).
В этом случае мы имеем простые проценты – это прообраз арифметической прогрессии. Постоянно за определённый промежуток времени (месяц, год) начисляется одна и та же сумма денег, определённая количеством процентов.
Другая ситуация, вы не снимаете ежегодно проценты по вкладу, а по истечении трех лет забираете деньги. Можно ли в этом случае связать проценты с прогрессией и какой?
Решим следующую задачу:
Начальный вклад клиента Сбербанка составил 10 000 рублей. Зная, что процентная ставка сбербанка 10%, определить, какая сумма будет на счете этого клиента: а) через год; б) через 2 года; в) через 3 года; г) через 10 лет.
Учащиеся без затруднений находят решение для задач а), б) и в), а при решении задачи г) у них возникает затруднение, т.к. они понимают, что их ждут огромные вычисления.
Учитель: Почему последняя задача вызывает у вас трудности?
(ответ: долго считать)
Учитель: А нельзя ли упростить процесс решения, сделать его менее трудоемким. Не находить суммы на счете за все предшествующие годы, а сразу получить выражение для этой суммы через 10 лет?
Учащиеся начинают выдвигать гипотезы, если таковых не оказывается, целесообразно рассмотреть дополнительную задачу, где учащиеся будут оперировать не чисто числовыми выражениями, а выражениями с переменной. Возможно, здесь легче увидеть некоторую закономерность. А затем вернемся к решению первой задачи под г).
Задача: Каждая линза в сложном объективе снижает световой поток на 5%. Сколько процентов светового потока останется после прохождения: одной линзы, двух линз, четырех линз?
Решение. Пусть х – количество светового потока.
5% от х – это 0,05х.
Тогда после прохождения одной линзы останется х – 0,05х = 0,95х.
5% от 0,95х – это 0,05*0,95х.
Тогда после прохождения второй линзы останется
0,95х – 0,05*0,95х = 0,95х*(1 – 0,05) = 0,952 х.
Рассуждая аналогично, приходим к следующему результату:
0,954 х – количество светового потока после прохождения четвертой линзы.
0,954 х  0,8145 х или 81% светового потока.
0,8145 х или 81% светового потока.
Учитель: Ну что, заметили закономерность? Попробуйте сформулировать ее и записать формулой.
Учащиеся: каждая следующая величина изменяется в одно и тоже число раз, т.е. это геометрическая прогрессия.
Учитель: А что является знаменателем этой геометрической прогрессии?
Учащиеся: Знаменателем прогрессии является 1 – р (для убывающей прогрессии) или 1 + р (для возрастающей прогрессии), если р – это десятичное выражение процентного числа.
Учитель: Попробуем теперь записать формулу для решения таких задач.
n
Учитель: Теперь вернемся к первой задаче.
Нам надо найти b10.
b10 = 10000 (1 +  )10 = 10000*1,110 = 10000*2,59374246
)10 = 10000*1,110 = 10000*2,59374246  259 37,42 руб.
259 37,42 руб.
Учитель: Такие проценты называют сложными – и здесь дело мы имеем с геометрической прогрессией.
Задача. На начало года товар стоил 200 руб. К концу каждого полугодия его цена увеличивалась на 5%. Сколько будет стоить товар к началу следующего года?
Ответ: 231,53 руб.
В наше время очень важно разбираться в процентных ставках банков, если вы хотите, как говориться, прогадать.
Для сравнения, рассмотрим следующую задачу:
Пусть имеется сумма 100 у.е.
Есть три банка, в которые можно положить деньги:
1 банк – простые проценты, из расчёта 3% в месяц.
2 банк – под простые проценты, из расчёта 40% в год.
3 банк – под сложные проценты, из расчёта 30% в год.
Мы хотим положить деньги на три года.
В каком банке это наиболее выгодно?
Класс делиться на три группы (три банка). Каждая группа решает свою задачу.
В процессе решения учитель оказывает консультативную помощь группам.
1 банк каждый месяц начисляет 3/100 от суммы 100,
то есть а1=100, d=0,03·100=3, n=37 (количество месяцев).
2 банк каждый год начисляет 0,4 от суммы 100 у.е., то есть
а1=100, d=0,4·100=40, n=4.
Под а1 – понимается сумма на начало года, поэтому
a4 – это сумма на конец третьего года.
3 банк даёт 30% в год. Это значит, что каждый год сумма увеличивается в 1,3 раза.
100%+30%. Здесь мы имеем дело с геометрической прогрессией.
b1=100, q=1,3, n=4.
Результаты подсчетов:
a37= 208 у.е.
a4= 220 у.е.
b4=219,7 у.е.
По окончании все результаты выводятся на экран и делается вывод, что выгоднее положить деньги во второй банк.
Учитель: «Дома произведите расчёты, если вложить деньги на 5 лет».
(Выгоднее в 3-м банке).
-
Домашнее задание.
-
Найти задачи, связанные с арифметической и геометрической прогрессией из различных областей: физики, медицины и т.д.
-
Решить задачу на проценты в банке (рассмотренную в классе), если вложить деньги в банк на 5 лет.
-
Итог урока.
-
В течение урока мы повторили основные формулы арифметической и геометрической прогрессий.
-
Решали нестандартные задачи, решение которых облегчает знание формул арифметической и геометрической прогрессий.
-
Оценка работы учащихся на уроке.
-
Рефлексия.
Урок сегодня завершён,
Дружней вас не сыскать.
Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут!
Спасибо за урок! До новых встреч!





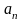 ) – арифметическая прогрессия,
) – арифметическая прогрессия, 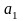 =-2,
=-2, 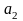 = 4.
= 4.  - ?
- ? ) – геометрическая прогрессия,
) – геометрическая прогрессия,  =2,
=2, 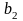 = 1.
= 1. 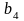 - ?
- ?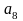 = 14.
= 14.  - ?
- ?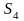 - ?
- ?