Параллельные прямые 7 класс

Решение задач.

"Параллельные

прямые"

теоремы параллельных прямых.

6

1

5

4

3

2

7

9

8

10

11

12

… по готовым рисункам

18

17

16

15

14

13

Задания на проверку теоретических знаний.

21

20

22

19

23

Свойства параллельных прямых.

25

28

29

27

24

26

… по готовым рисункам

30

32

31

33

34

Параллельные прямые.

Определение.

а

b

Две прямые на плоскости называются

ПАРАЛЛЕЛЬНЫМИ , если они не пересекаются.

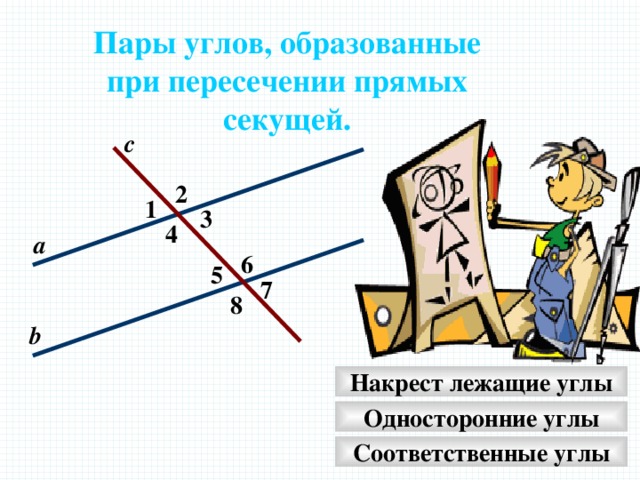
Пары углов, образованные

при пересечении прямых

секущей.

с

2

1

3

4

а

6

5

7

Р

8

b

Накрест лежащие углы

Односторонние углы

Соответственные углы

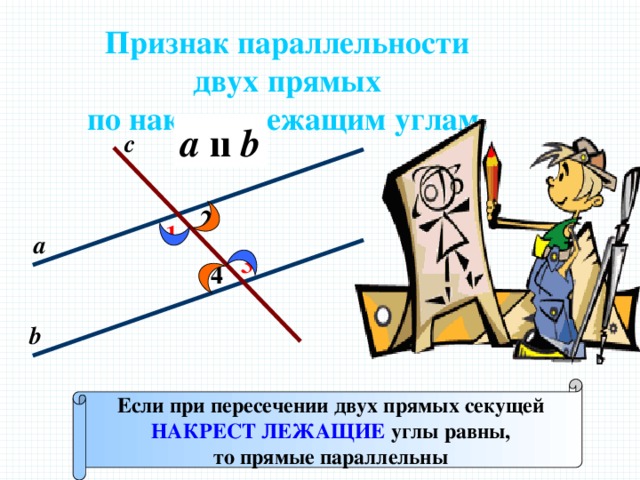
Признак параллельности

двух прямых

по накрест лежащим углам.

a ıı b

с

2

1

а

3

4

Р

b

Если при пересечении двух прямых секущей

НАКРЕСТ ЛЕЖАЩИЕ углы равны,

то прямые параллельны

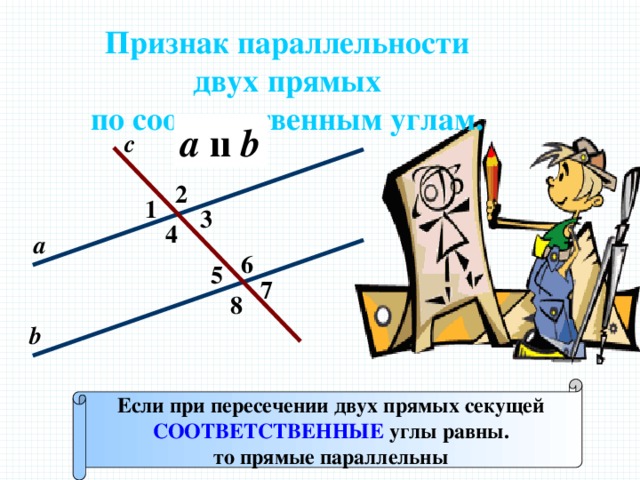
Признак параллельности

двух прямых

по соответственным углам.

a ıı b

с

2

1

3

4

а

6

5

7

Р

8

b

Если при пересечении двух прямых секущей

СООТВЕТСТВЕННЫЕ углы равны.

то прямые параллельны

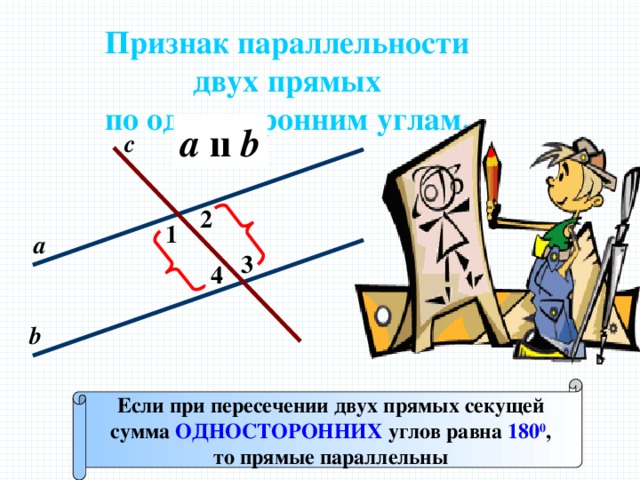
Признак параллельности

двух прямых

по односторонним углам.

a ıı b

с

2

1

а

3

4

Р

b

Если при пересечении двух прямых секущей

сумма ОДНОСТОРОННИХ углов равна 180 0 ,

то прямые параллельны

Аксиома параллельных прямых.

а

А

b

Через точку, не лежащую на данной прямой,

проходит только одна прямая,

параллельная данной.

Следствие из аксиомы

параллельных прямых.

1 0

a ıı b

с

а

b

Если прямая пересекает одну из двух

параллельных прямых, то она

пересекает и другую.

Следствие из аксиомы

параллельных прямых.

2 0

а

с

b

a ıı b

Если две прямые параллельны третьей прямой,

то они параллельны.

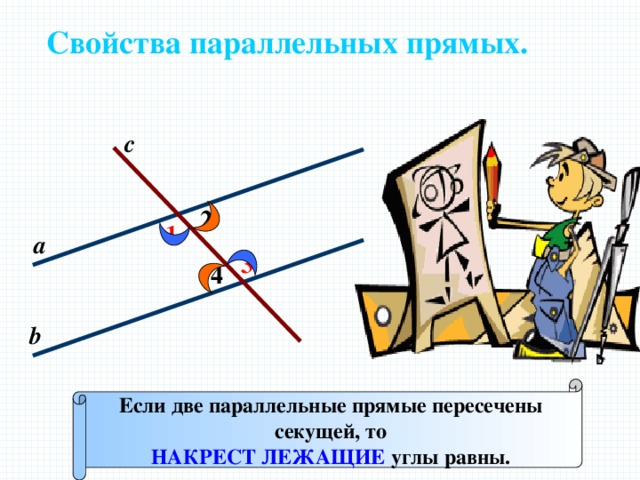
Свойства параллельных прямых.

с

2

1

а

3

4

Р

b

Если две параллельные прямые пересечены

секущей, то

НАКРЕСТ ЛЕЖАЩИЕ углы равны.

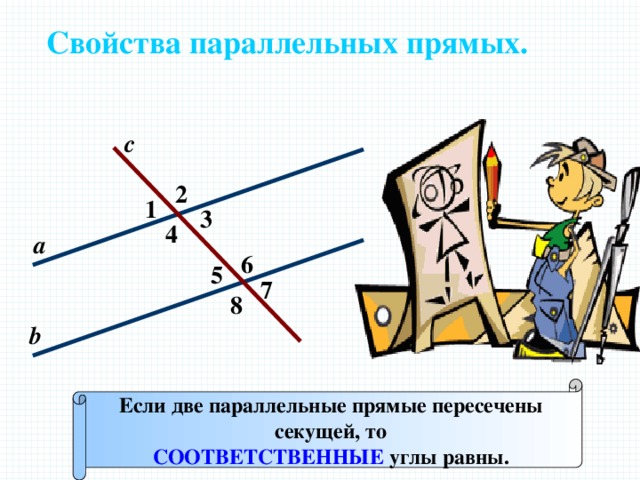
Свойства параллельных прямых.

с

2

1

3

4

а

6

5

7

Р

8

b

Если две параллельные прямые пересечены

секущей, то

СООТВЕТСТВЕННЫЕ углы равны.

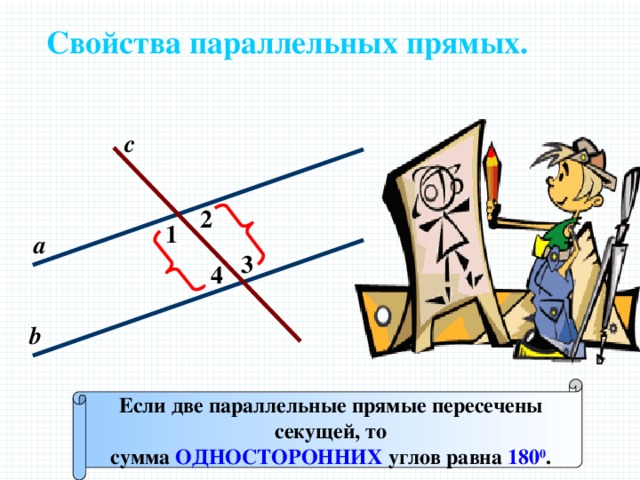
Свойства параллельных прямых.

с

2

1

а

3

4

Р

b

Если две параллельные прямые пересечены

секущей, то

сумма ОДНОСТОРОННИХ углов равна 180 0 .

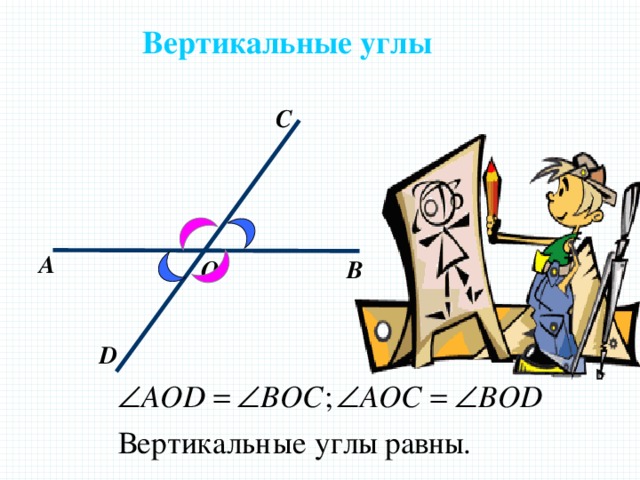
Вертикальные углы

C

А

В

О

D

Смежные углы

В

А

О

C

Свойства параллельных прямых.

Необходимо по условию

задачи отметить все

на рисунке, и ответить

на поставленный вопрос,

используя свойства

параллельных прямых.

1

6

5

3

4

2

7

8

9

10

11

12

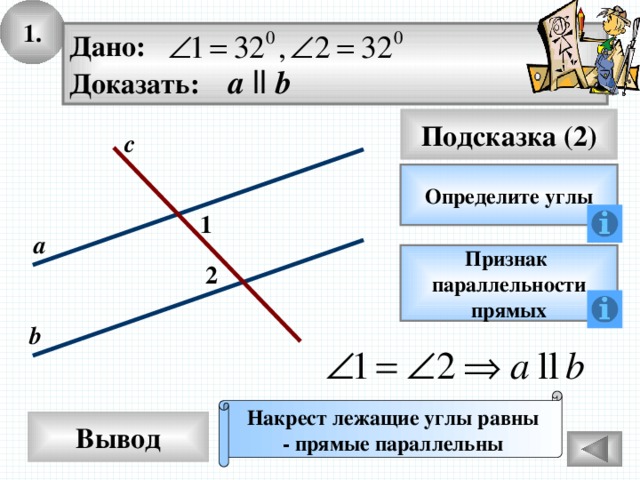
1.

Дано:

Доказать: а ll b

Подсказка (2)

с

Определите углы

1

а

Признак

параллельности

прямых

2

b

Накрест лежащие углы равны

- прямые параллельны

Вывод

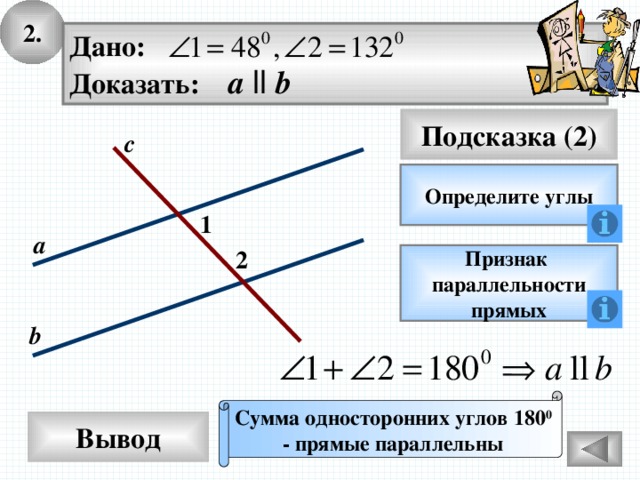
2.

Дано:

Доказать: а ll b

Подсказка (2)

с

Определите углы

1

а

2

Признак

параллельности

прямых

b

Сумма односторонних углов 180 0

- прямые параллельны

Вывод

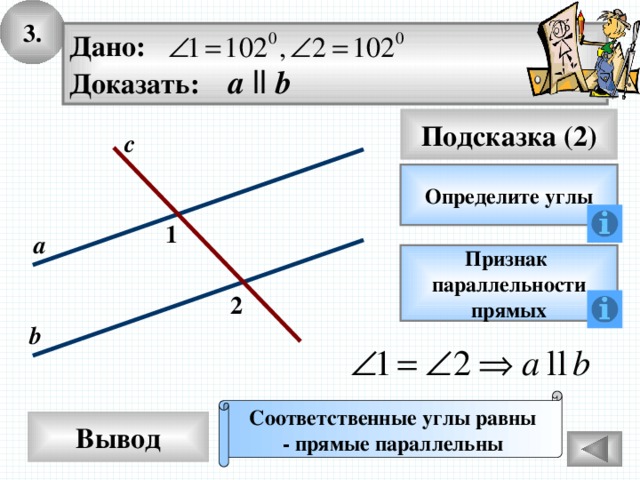
3.

Дано:

Доказать: а ll b

Подсказка (2)

с

Определите углы

1

а

Признак

параллельности

прямых

2

b

Соответственные углы равны

- прямые параллельны

Вывод

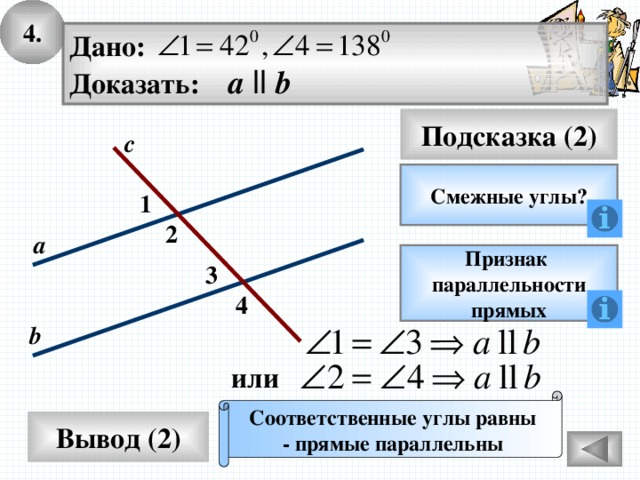
4.

Дано:

Доказать: а ll b

Подсказка (2)

с

Смежные углы?

1

2

а

Признак

параллельности

прямых

3

4

b

или

Соответственные углы равны

- прямые параллельны

Вывод (2)

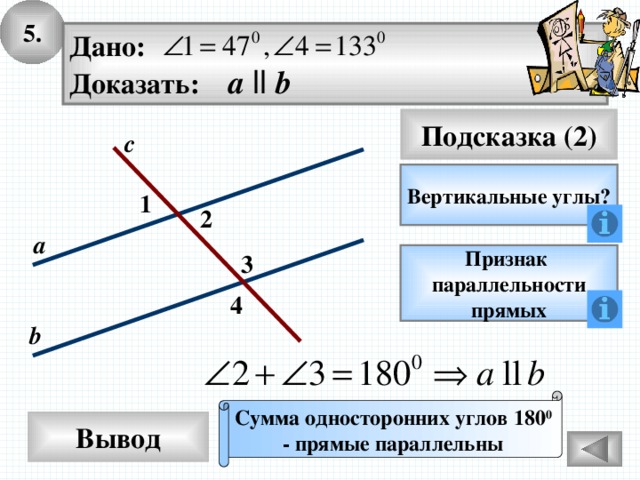
5.

Дано:

Доказать: а ll b

Подсказка (2)

с

Вертикальные углы?

1

2

а

3

Признак

параллельности

прямых

4

b

Сумма односторонних углов 180 0

- прямые параллельны

Вывод

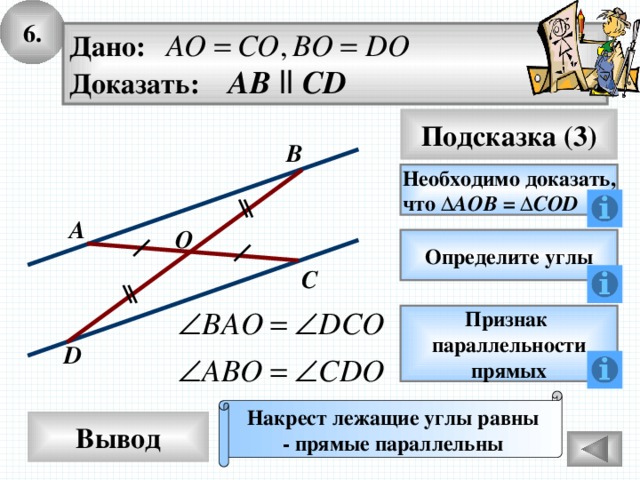
6.

Дано:

Доказать: AB ll CD

Подсказка (3)

B

Необходимо доказать,

что Δ АОВ = Δ COD

A

O

Определите углы

C

Признак

параллельности

прямых

D

Накрест лежащие углы равны

- прямые параллельны

Вывод

7.

Дано:

Доказать: a ll c

Подсказка (3)

1

a

Углы 1 и 2…

Признак?

2

b

4

Определите углы

3 и 2

c

3

d

Следствие из аксиомы

параллельных

прямых

Если две прямые параллельны

третьей прямой, то они

параллельны

Вывод

8.

Дано:

Доказать: a ll c

Подсказка (3)

1

a

4

Вертикальные

углы

2

b

Определите углы

3 и 2

3

c

d

Следствие из аксиомы

параллельных

прямых

Если две прямые параллельны

третьей прямой, то они

параллельны

Вывод

9.

Дано:

Какие из прямых параллельны?

Подсказка (3)

1

a

Вертикальные

углы

b

2

Смежные углы

c

3

d

Виды углов

Вывод

10.

Дано:

Доказать: m ll n

Подсказка (3)

m

1

3

Вертикальные углы

Определите углы

3 и 2

n

2

Признак

параллельности

прямых

Сумма односторонних углов 180 0

- прямые параллельны

Вывод

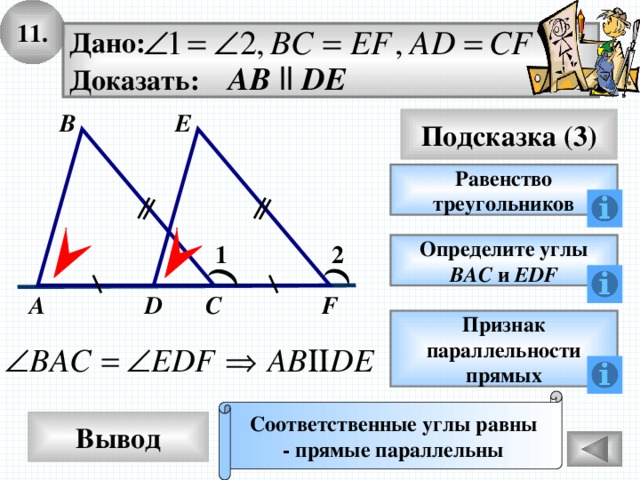
11.

Дано:

Доказать: AB ll DE

E

В

Подсказка (3)

Равенство

треугольников

1

2

Определите углы

ВАС и EDF

С

D

F

А

Признак

параллельности

прямых

Соответственные углы равны

- прямые параллельны

Вывод

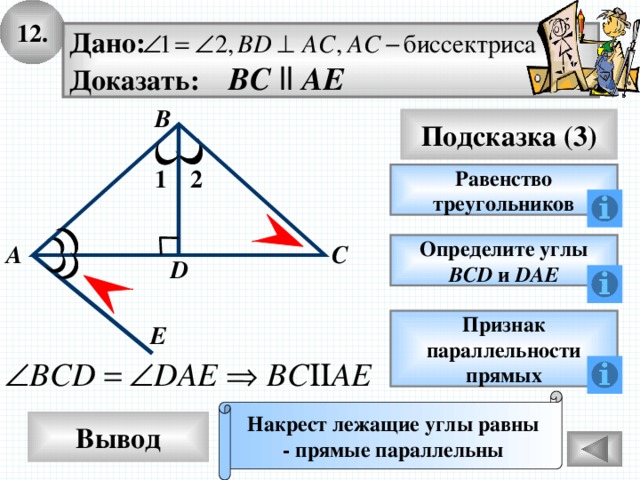
12.

Дано:

Доказать: BС ll АE

В

Подсказка (3)

2

1

Равенство

треугольников

С

А

Определите углы

ВСD и DAE

D

Признак

параллельности

прямых

E

Накрест лежащие углы равны

- прямые параллельны

Вывод

Решение задач

по готовым рисункам.

Необходимо по рисунку

записать условие задачи

и ответить на поставленный

вопрос.

14

15

16

13

17

18

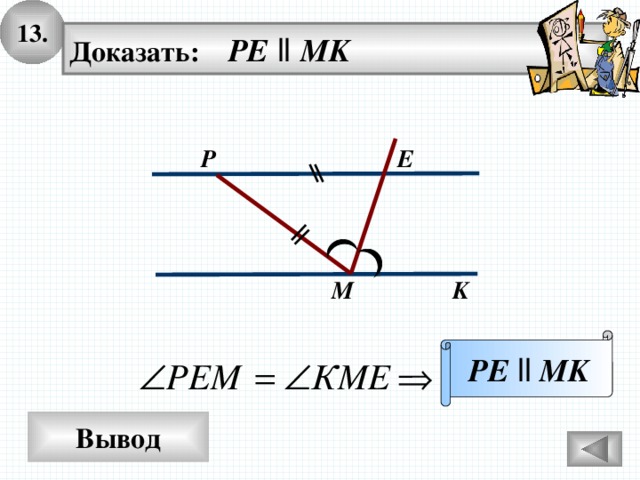
13.

Доказать: PE ll MK

E

P

M

K

PE ll MK

Вывод

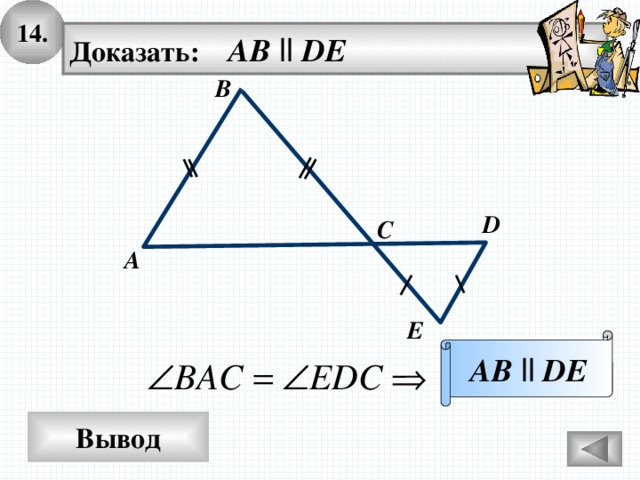
14.

Доказать: AB ll DE

B

D

C

A

E

AB ll DE

Вывод

15.

Доказать: AB ll MN

N

В

K

M

С

А

AB ll MN

Вывод

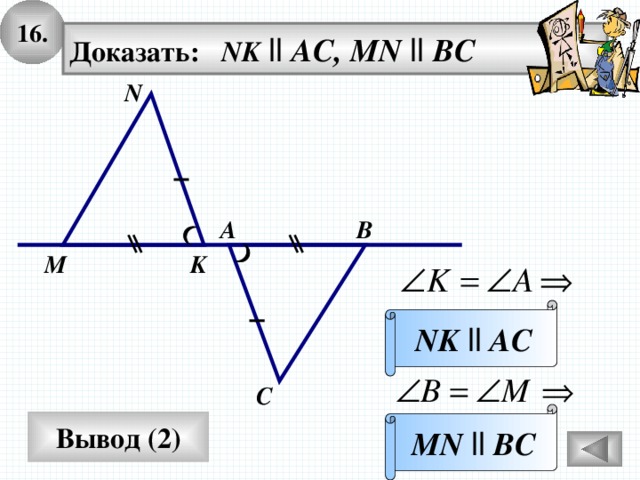
16.

Доказать: NK ll AC, MN ll BC

N

А

В

K

M

NK ll AC

С

MN ll BC

Вывод (2)

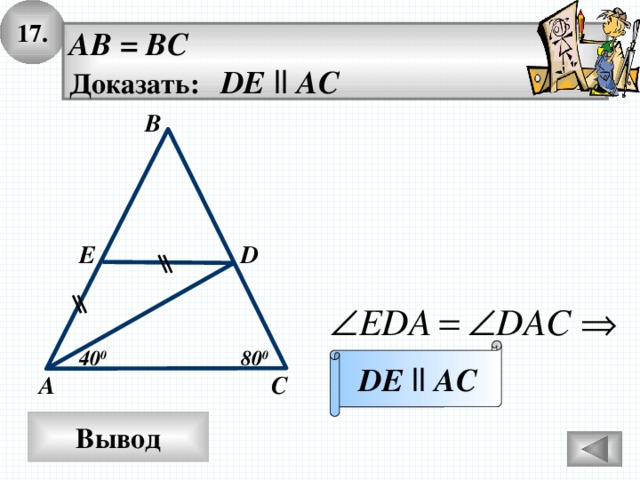
17.

AB = BC

Доказать: DE ll AC

В

D

E

DE ll AC

80 0

40 0

А

С

Вывод

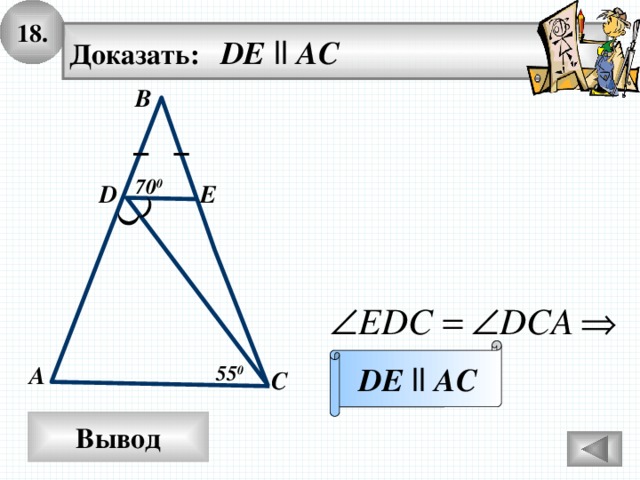
18.

Доказать: DE ll AC

В

70 0

E

D

DE ll AC

55 0

А

С

Вывод

Тестовые задания на

проверку теоретических знаний.

В заданиях 19 и 20 необходимо

выбрать верные утверждения.

В 21 задании необходимо указать

продолжение высказывания,

НЕ соответствующее

действительности.

В 22 и 23 заданиях кратко

ответить на вопрос и дать

пояснение к ответу

20

21

19

22

23

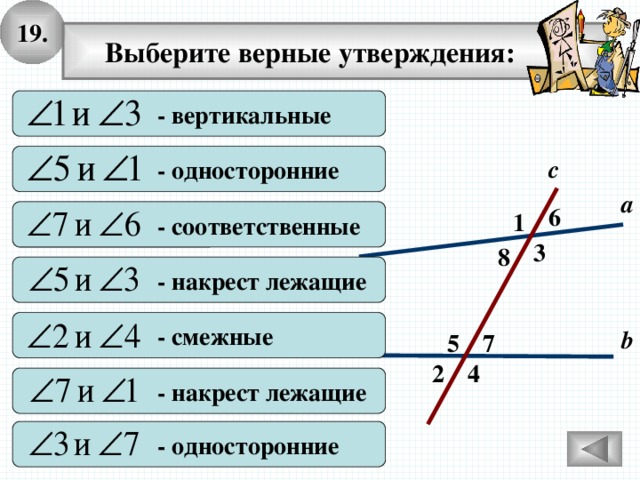
19.

Выберите верные утверждения:

- вертикальные

- односторонние

с

а

6

- соответственные

1

3

8

- накрест лежащие

- смежные

b

7

5

4

2

- накрест лежащие

- односторонние

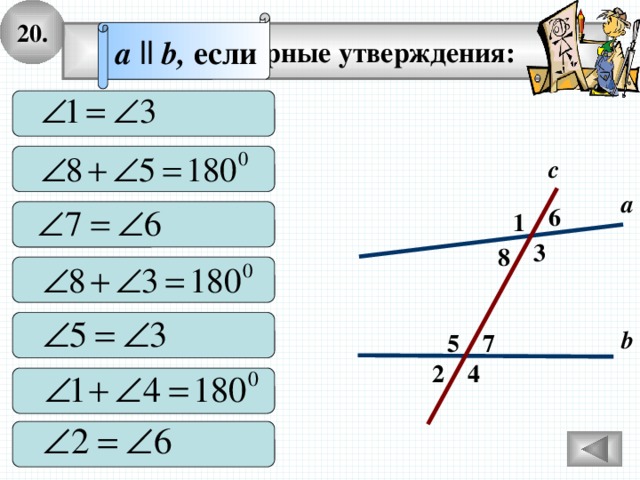
20.

a ll b, если

Выберите верные утверждения:

с

а

6

1

3

8

b

7

5

2

4

21.

НЕ СООТВЕТСТВУЕТ

Прямые не параллельны, если при

пересечении двух прямых секущей:

сумма односторонних углов не равна 180 0 .

сумма соответственных углов равна 180 0 .

вертикальные углы равны .

накрест лежащие углы не равны .

сумма смежных углов не равна 180 0 .

соответственные углы не равны .

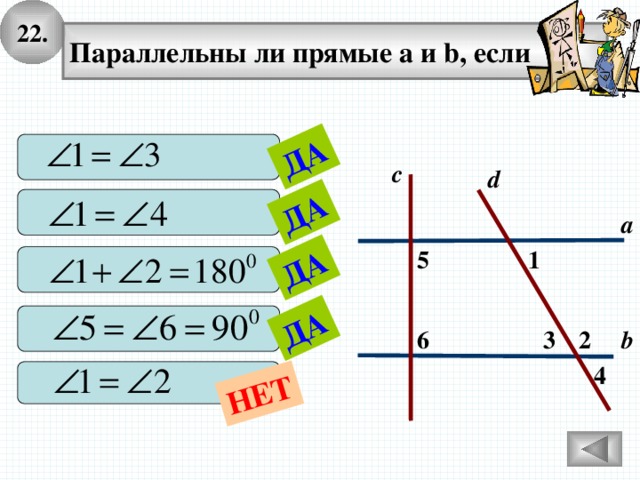
22.

ДА

ДА

ДА

ДА

НЕТ

Параллельны ли прямые а и b, если

с

d

а

5

1

2

b

6

3

4

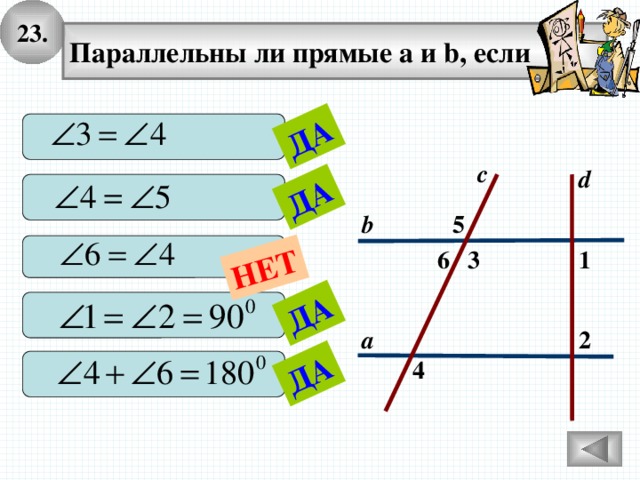
23.

ДА

ДА

ДА

ДА

НЕТ

Параллельны ли прямые а и b, если

с

d

5

b

6

3

1

2

а

4

Свойства параллельных прямых.

Необходимо по условию

задачи отметить все

на рисунке, и ответить

на поставленный вопрос,

используя свойства

параллельных прямых.

25

26

27

28

29

24

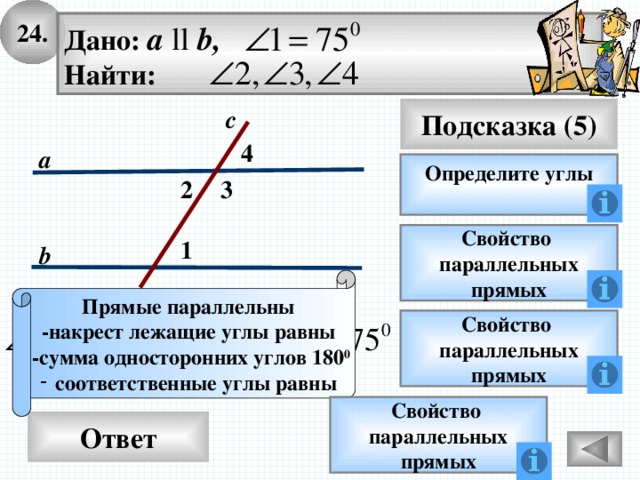
24.

Дано: а ll b,

Найти:

Подсказка (5)

с

4

а

Определите углы

2

3

Свойство

параллельных

прямых

1

b

Прямые параллельны

-накрест лежащие углы равны

-сумма односторонних углов 180 0

• соответственные углы равны

Свойство

параллельных

прямых

Свойство

параллельных

прямых

Ответ

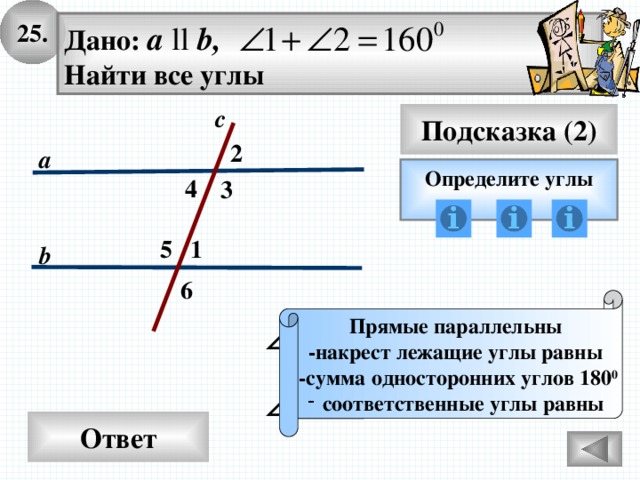
25.

Дано: а ll b,

Найти все углы

с

Подсказка (2)

2

а

Определите углы

4

3

5

1

b

6

Прямые параллельны

-накрест лежащие углы равны

-сумма односторонних углов 180 0

• соответственные углы равны

Ответ

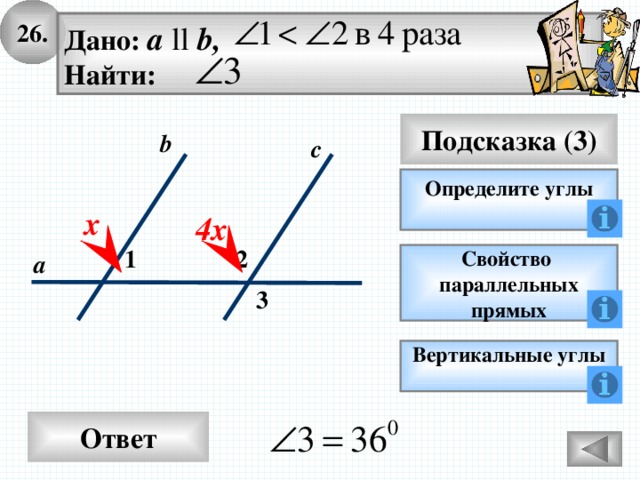
26.

Дано: а ll b,

Найти:

Подсказка (3)

b

с

Определите углы

х

4х

2

1

а

Свойство

параллельных

прямых

3

Вертикальные углы

Ответ

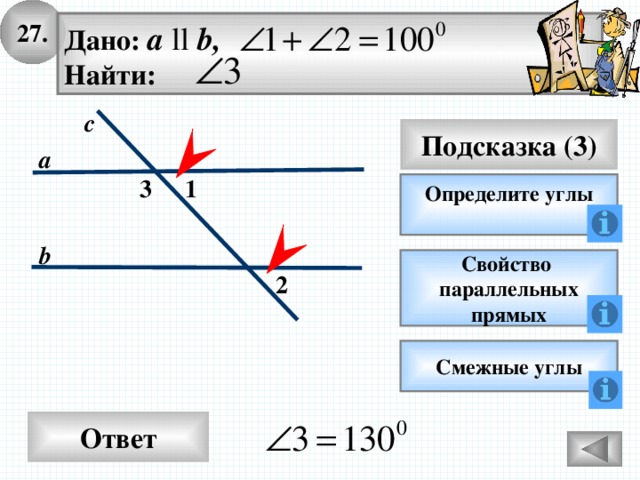
27.

Дано: а ll b,

Найти:

с

Подсказка (3)

а

3

1

Определите углы

b

Свойство

параллельных

прямых

2

Смежные углы

Ответ

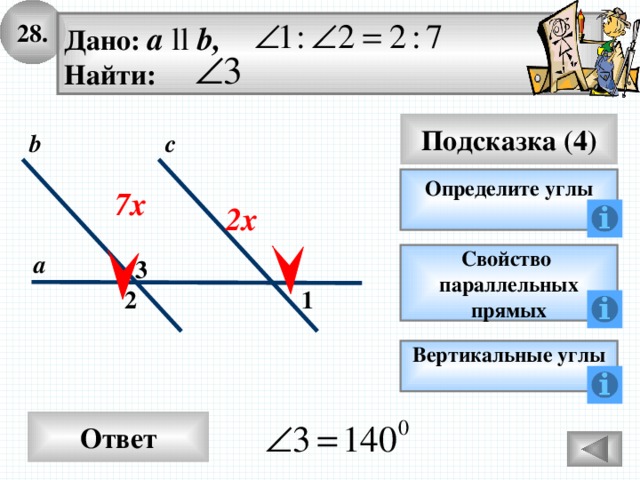
28.

Дано: а ll b,

Найти:

Подсказка (4)

с

b

Определите углы

7х

2х

а

Свойство

параллельных

прямых

3

2

1

Вертикальные углы

Ответ

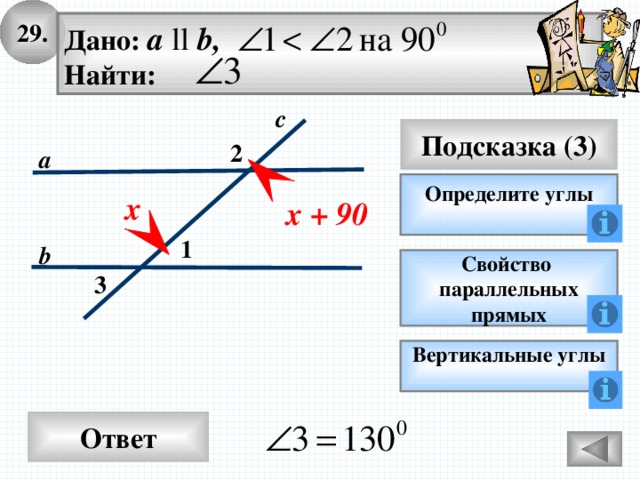
29.

Дано: а ll b,

Найти:

с

Подсказка (3)

2

а

Определите углы

х

х + 90

1

b

Свойство

параллельных

прямых

3

Вертикальные углы

Ответ

Решение задач

по готовым рисункам.

Необходимо по рисунку

записать условие задачи

и ответить на поставленный

вопрос.

31

32

33

30

34

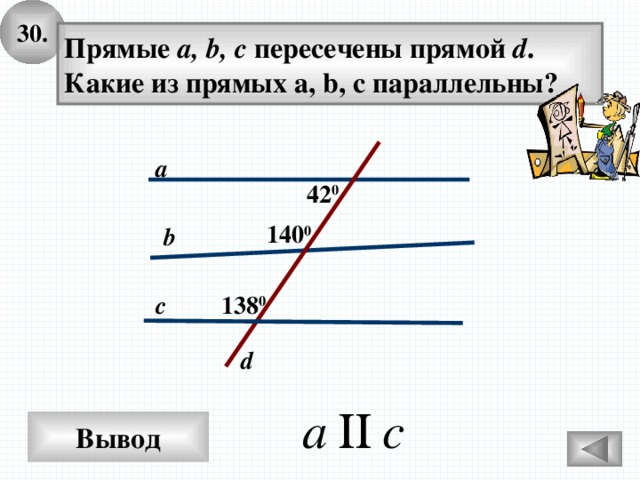
30.

Прямые а, b, c пересечены прямой d .

Какие из прямых a, b, c параллельны?

a

42 0

140 0

b

c

138 0

d

Вывод

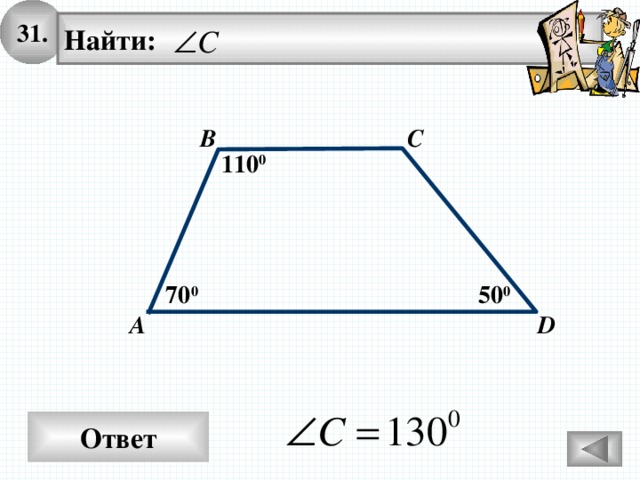
31.

Найти:

С

В

110 0

50 0

70 0

А

D

Ответ

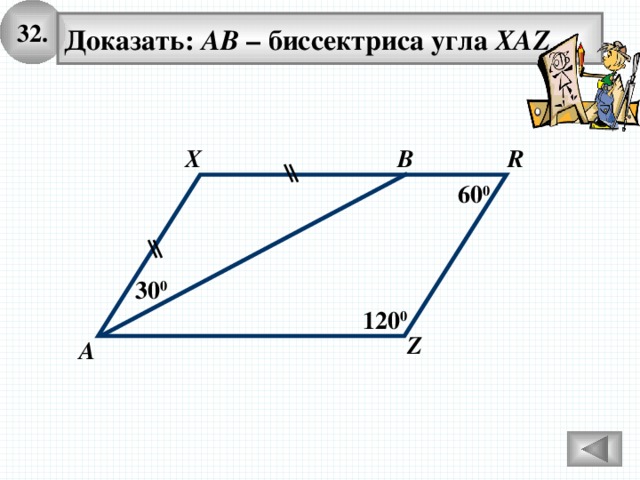
32.

Доказать: АВ – биссектриса угла XAZ

В

R

X

60 0

30 0

120 0

Z

А

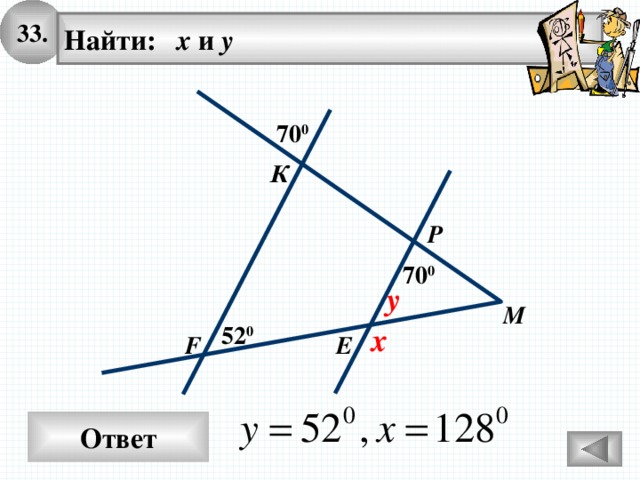
33.

Найти: х и у

70 0

К

Р

70 0

y

М

x

52 0

F

Е

Ответ

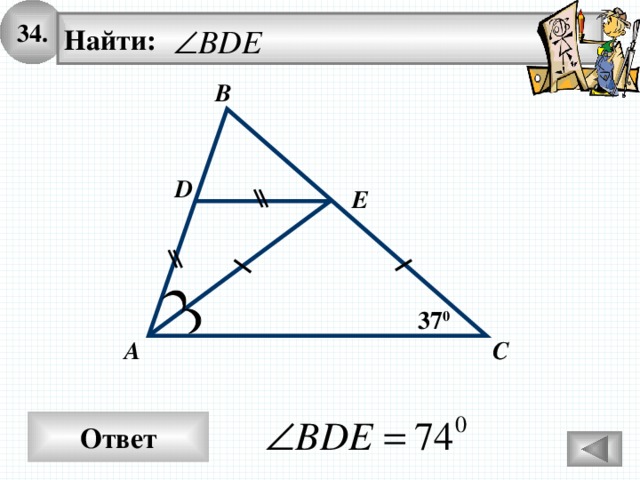
34.

Найти:

В

D

E

37 0

А

С

Ответ

Первый признак

равенства треугольников.

А 1

А

В

С 1

С

В 1

По двум сторонам и углу между ними.

Второй признак

равенства треугольников.

А

А 1

В 1

С

В

С 1

По стороне и прилежащим к ней углам.

Третий признак

равенства треугольников.

А

А 1

С 1

С

В 1

В

По трём сторонам.

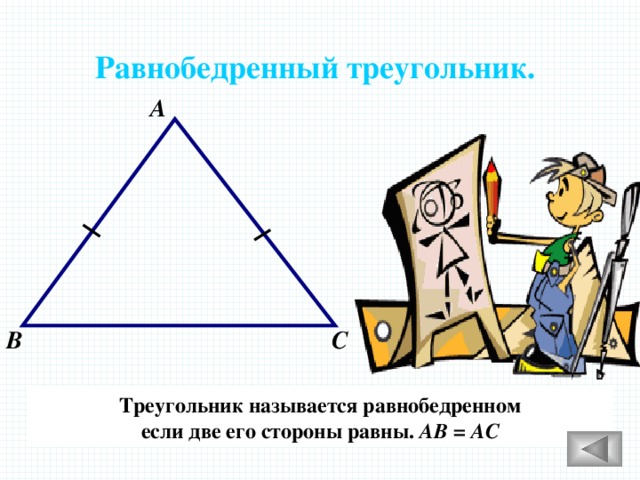
Равнобедренный треугольник.

А

В

С

Треугольник называется равнобедренном

если две его стороны равны. АВ = АС

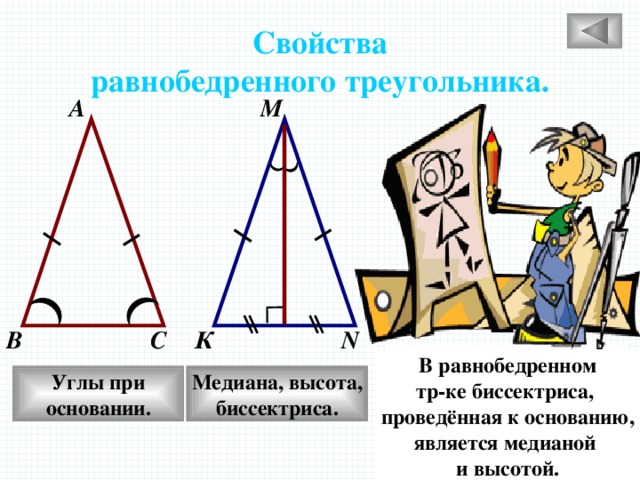
Свойства

равнобедренного треугольника.

А

М

В

С

N

К

В равнобедренном

треугольнике углы

при основании равны.

В равнобедренном

тр-ке биссектриса,

проведённая к основанию,

является медианой

и высотой.

Медиана, высота,

Углы при

основании.

биссектриса.

Спасибо за внимание!!!"