Пределы. Непрерывность функций

Пределы. Непрерывность функций

Введение

Цель работы:

1. Совершенствовать уровень своей математической подготовки.

2. Овладеть некоторыми вопросами математического анализа.

Задачи исследования:

1. Изучить определения и свойства предела, непрерывность функции.

2. Выработать навыки нахождения пределов, построения графи-ков разрывных функций.

Актуальность темы:

Изучение данной темы предусматривает межпредметную связь математики и физики. Понятие предела непосредственно связано с ос-новными понятиями математического анализа – производная, инте-грал и др.

Предел переменной величины

Пределом переменной величины х называется постоянное число а , если для каждого наперед заданного произвольно малого положи-тельного числа ε можно указать такое значение переменной х , что все последующие значения будут удовлетворять неравенству | х –а | а есть предел переменной величины х , то пишут: lim x=a.

В терминах геометрических определение предела может быть сформулировано следующим образом: постоянное число а есть пре-дел переменной х , если для любой наперед заданной как угодно малой окрестности с центром в точке а и радиусом ε найдется такое значе-ние х , что все точки, соответствующие последующим значениям пере-менной, будут находиться в этой окрестности:

2ε

а

0

х

ε

, будут удовлетворять условию | х n –1 | Пример 2. Доказать, что переменная w n = (-1) n при неогра-ниченном возрастании n не имеет предела. Действительно, при возрастании n , переменная w n не стремится ни к какому числу, попеременно принимая значения 1 и –1, т. е. не имеет предела. " width="640"

Предел переменной величины

Рассмотрим несколько примеров переменных, стремящихся к пределу.

Пример 1. Доказать, что переменная х n =1+ имеет предел, равный единице.

Составим разность между переменной и ее пределом: | х n –1|=|(1+ )–1|= . Для любого ε все последующие значения перемен-ной, начиная с номера n , где n , будут удовлетворять условию | х n –1 |

Пример 2. Доказать, что переменная w n = (-1) n при неогра-ниченном возрастании n не имеет предела.

Действительно, при возрастании n , переменная w n не стремится ни к какому числу, попеременно принимая значения 1 и –1, т. е. не имеет предела.

а , то пишут ƒ ( х ) = b 2 . Числа b 1 и b 2 называются соот-ветственно левым и правым пределом функции у = ƒ ( х ). " width="640"

Предел функции

Пределом функции ƒ ( х ) при х→а называется число b , если для любого положительного ε можно указать такое положительное число δ , что для любого х , удовлетворяющего неравенству | х –а ||f(x)–b| ε . В этом случае пишут: ƒ ( х ) = b .

Если х→а и х , то употребляют запись ƒ ( х ) = b 1 ; если же х→а , но ха , то пишут ƒ ( х ) = b 2 . Числа b 1 и b 2 называются соот-ветственно левым и правым пределом функции у = ƒ ( х ).

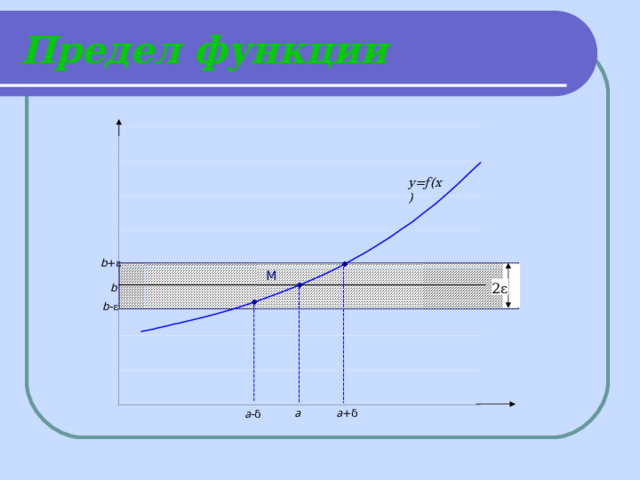
Предел функции

y=ƒ (х)

b +ε

М

2ε

b

b - ε

a

a +δ

a -δ

Основные свойства пределов

Свойство 1. Предел суммы нескольких переменных равен сумме пределов этих переменных:

lim( a 1 +a 2 +…+a n ) = lim  a 1 +lim  a 2 +…+lim  a n .

Свойство 2. Предел произведения нескольких переменных равен произведению пределов этих переменных: lim( a 1 ∙ a 2 ∙ … ∙ a n ) = lim  a 1 ∙ lim  a 2 ∙ … ∙ lim  a n .

Свойство 3. Предел частного двух переменных равен част-ному пределов этих переменных, если предел знаменателя отли-чен от нуля: lim = , если lim  b ≠0.

Свойство 4. Предел степени равен пределу основания, воз-веденного в степень предела показателя: lim  a b = (lim  a ) lim  b .

Основные свойства пределов

Первый замечательный предел:

Второй замечательный предел:

Далее я решил привести некоторые часто встречающиеся типы примеров, рассмотренных мной в ходе работы:

1 .

2.

Основные свойства пределов

3.

4.

Основные свойства пределов

5.

6.

Пусть и=2+а, а→0.

Непрерывность функций

Функция называется непрерывной в точке х 0 , если она определена в некоторой окрестности этой точки и существует предел функции при х→х 0 , равный значению самой функции в этой точке. Функция на-зывается непрерывной в некоторой области, если она непрерывна в каждой точке этой области. Точка х 0 , принадлежащая области опреде-ления функции, называется точкой разрыва, если в этой точки нару-шается условие непрерывности. Если существуют конечные левый и правый пределы функции в точке х 0 , а функции определена в этой точке, но эти три числа не равны между собой, то точка х 0 называется точкой разрыва I рода. Точки разрыва, не являющиеся точками разры-ва I рода, называются точками разрыва II рода.

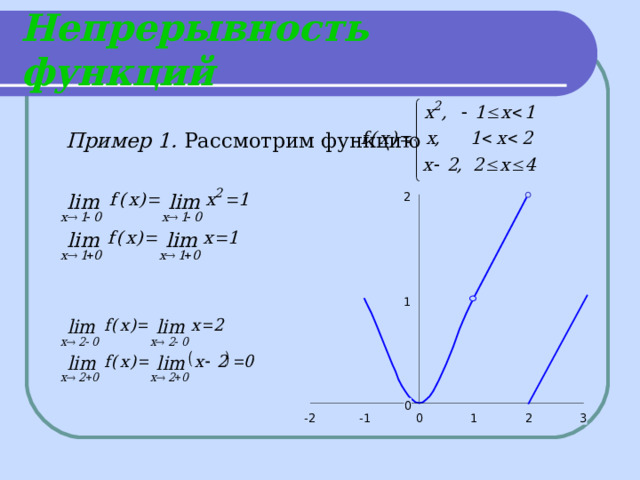
Непрерывность функций

Пример 1. Рассмотрим функцию

2

1

0

2

1

0

-1

-2

3

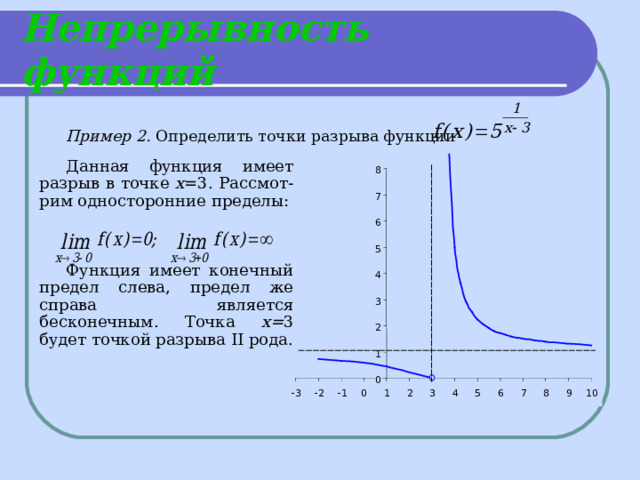
Непрерывность функций

Пример 2. Определить точки разрыва функции

Данная функция имеет разрыв в точке х =3. Рассмот-рим односторонние пределы:

Функция имеет конечный предел слева, предел же справа является бесконечным. Точка х= 3 будет точкой разрыва II рода.

8

7

6

5

4

3

2

1

0

10

9

7

8

6

5

4

3

2

1

0

-2

-3

-1