Презентация "Геометрическая задача на вычисление, подготовка к ОГЭ"

Приёмы решения геометрических задач второй части

Учитель математики

МАОУ Каскаринской СОШ Ленский Александр Петрович

Трудности решения геометрических задач

• Неалгоритмичность задач
• Необходимость выбора метода решения задачи и теоремы для решения конкретной задачи (нескольких теорем) из большого набора известных фактов
• Нужно решить довольно много задач, чтобы научиться их решать.

Необходимые условия успеха при решении задач по геометрии

• Уверенное владение основными понятиями и их свойствами (определения, аксиомы, теоремы, базовые задачи)
• Знание основных методов и приёмов решения задач
• Умение комбинировать методы и приёмы решения задач
• Наличие опыта решения задач

Причины ошибок в решении геометрических задач

• Незнание и/или непонимание аксиом, определений, теорем
• Неумение их применять
• Невнимательное чтение условия и вопроса задания
• Вычислительные ошибки
• Нарушения логики в рассуждениях
• Принятие ошибочных гипотез
• Недостатки в работе с рисунком

Специфические особенности методов решения геометрических задач

• Большое разнообразие
• Взаимозаменяемость
• Трудность формального описания
• Отсутствие чётких границ применения (в отличие от алгебры)
• Использованию комбинаций методов и приёмов .

Некоторые методы решения геометрических задач второй части ОГЭ

• Применение ключевых задач
• Метод вспомогательных построений
• Переход к равновеликим фигурам
• Метод площадей

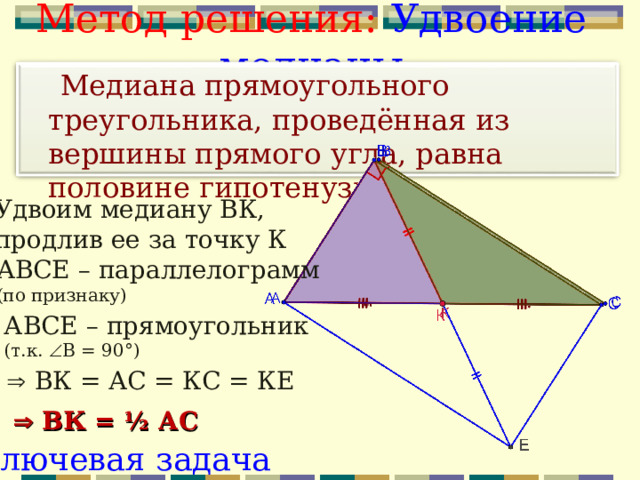
Метод решения: Удвоение медианы

Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Удвоим медиану ВК,

продлив ее за точку К

АВСЕ – параллелограмм

(по признаку)

АВСЕ – прямоугольник

(т.к.  В = 90°)

 ВК = АС = КС = КЕ

 ВК = ½ АС

Ключевая задача

Следствие из свойства медианы к гипотенузе. Ключевая задача

Медиана прямоугольного треугольника, проведённая к гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника

Использование введения буквенных обозначений величин. Ключевая задача

Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный .

∆ ABD и ∆ BCD – равнобедренные

 BAD =  ABD = α ;  DBC =  BCD = β

2 α + 2 β =180 °

α + β =90 °

 АВС = α + β = 90 °

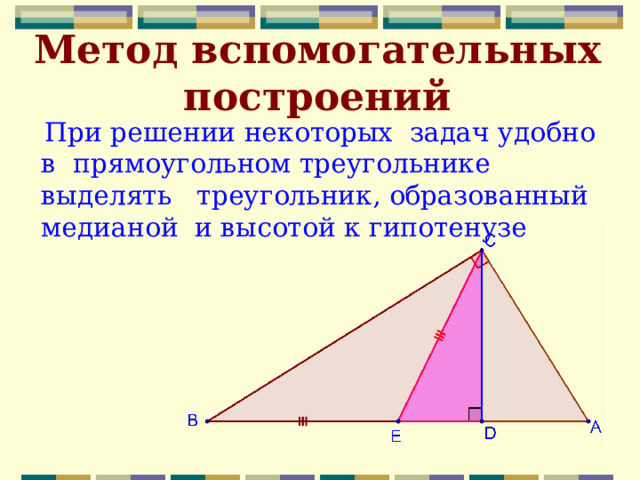
Метод вспомогательных построений

При решении некоторых задач удобно в прямоугольном треугольнике выделять треугольник, образованный медианой и высотой к гипотенузе

Применение свойства медианы к гипотенузе

Найдите гипотенузу прямоугольного треугольника с острым углом 15°, если известно, что высота треугольника, опущенная на гипотенузу, равна 1.

Проведем медиану CD к гипотенузе.

∆ ACD - равнобедренный

 CAD =  ACD = 15°

Применение свойства медианы к гипотенузе

Найдите гипотенузу прямоугольного треугольника с острым углом 15°, если известно, что высота треугольника, опущенная на гипотенузу, равна 1.

 CAD =  ACD = 15°

 CDH = 30° как внешний угол

CD = 2 СН = 2

АВ = 2 С D = 4

Ответ: 4

12

Применение свойства медианы к гипотенузе

Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18.

Проведем медиану CD и высоту СН к гипотенузе.

С D = 6

  CDH = 30°

  CAD =  ACD = 15°

 C ВА = 90° - 15° = 75°

Ответ: 15°; 75°

Свойства площади треугольника

Площади треугольников, имеющих общую высоту (равные высоты) , относятся как стороны, к которым эти высоты проведены

2. Медиана делит треугольник на два равновеликих треугольника

Ключевые задачи

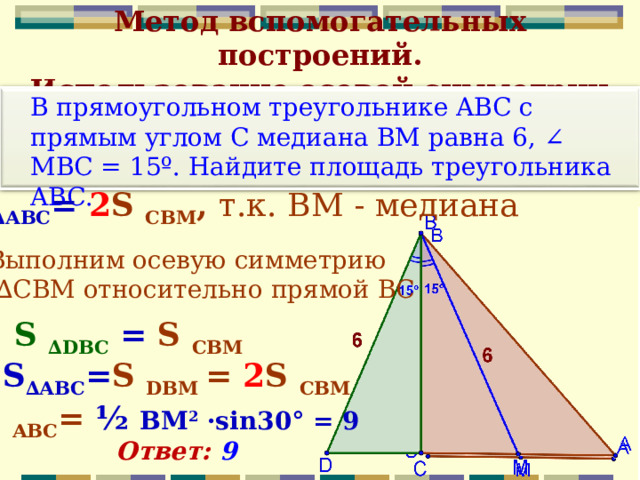
Метод вспомогательных построений. Использование осевой симметрии

В прямоугольном треугольнике ABC c прямым углом С медиана BM равна 6, ∠ MBC = 15º. Найдите площадь треугольника ABC.

S ∆ АВС = 2 S CB М , т.к. ВМ - медиана

Выполним осевую симметрию

∆ СВМ относительно прямой ВС

S ∆D В C = S CB М

S ∆ АВС = S DB М = 2 S CB М

S ABC = ½ ВМ 2 · sin30° = 9

Ответ: 9

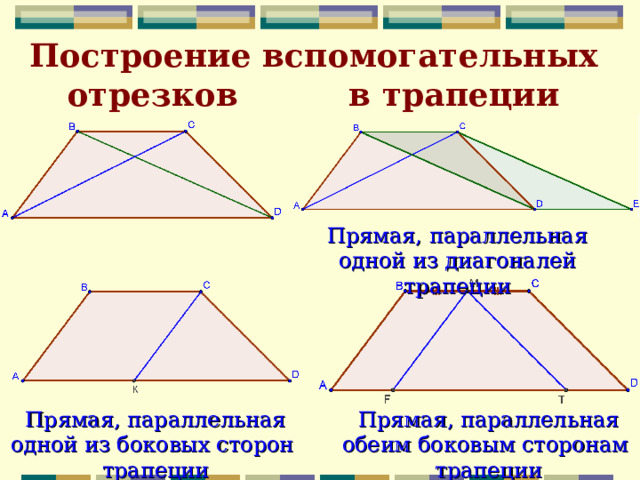
Построение вспомогательных отрезков в трапеции

Прямая, параллельная одной из диагоналей трапеции

Прямая, параллельная одной из боковых сторон трапеции

Прямая, параллельная обеим боковым сторонам трапеции

Медиана прямоугольного треугольника к гипотенузе

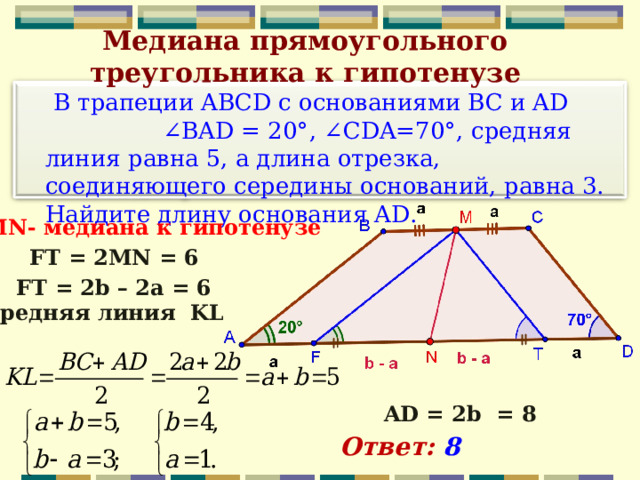
В трапеции ABCD с основаниями BC и AD ∠BAD = 20°, ∠CDA=70°, средняя линия равна 5, а длина отрезка, соединяющего середины оснований, равна 3. Найдите длину основания AD.

AD – большее основание

Построим MF ║AB, MT ║ CD

Применение свойства медианы к гипотенузе

В трапеции ABCD с основаниями BC и AD ∠BAD = 20°, ∠CDA=70°, средняя линия равна 5, а длина отрезка, соединяющего середины оснований, равна 3. Найдите длину основания AD.

 FMT - прямой

∆ FMT - прямоугольный

MN - медиана?

Обозначим AN = NB = b;

AD = 2b, BM = MC = a

 MN - медиана к гипотенузе

 FT = 2MN = 6

Медиана прямоугольного треугольника к гипотенузе

В трапеции ABCD с основаниями BC и AD ∠BAD = 20°, ∠CDA=70°, средняя линия равна 5, а длина отрезка, соединяющего середины оснований, равна 3. Найдите длину основания AD.

MN - медиана к гипотенузе

FT = 2MN = 6

FT = 2b – 2a = 6

средняя линия KL

AD = 2b = 8

Ответ: 8

Метод решения : Переход к равновеликой вспомогательной фигуре

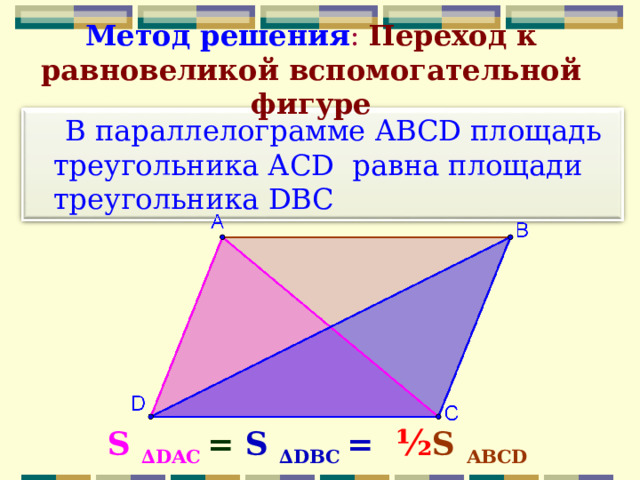
В параллелограмме ABCD площадь треугольника АС D равна площади треугольника DB С

S ∆DAC = S ∆D В C = ½ S ABCD

Метод решения : Переход к равновеликой вспомогательной фигуре

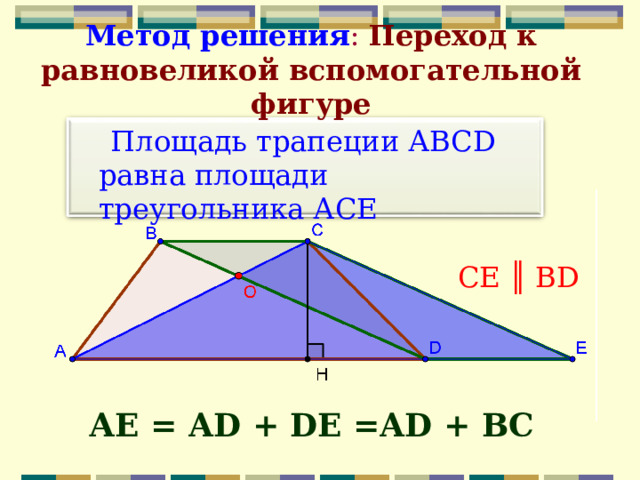
Площадь трапеции АВС D равна площади треугольника АСЕ

CE ║ BD

АЕ = AD + DE =AD + ВС

Дополнительные построения в трапеции

Переход к равновеликой вспомогательной фигуре

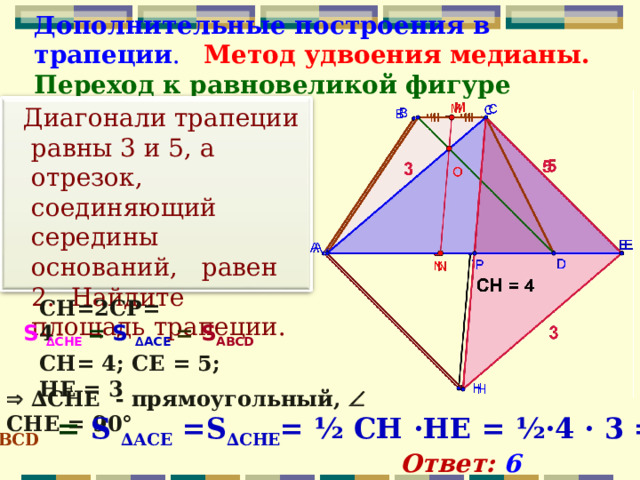
Диагонали трапеции равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции.

Проведем CE ║ BD , СР ║ MN

S ABCD = S ∆ А C Е

Дополнительные построения в трапеции.

Диагонали трапеции равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции .

СР – медиана ?

Обозначим ВМ = MC = а;

А N = ND = b

MC = NP = а; BC = DE = 2a

PD = b - a

AP = b + а; PE = b – a+2a = b + a

 СР – медиана к гипотенузе

Применим метод удвоения медианы

Дополнительные построения в трапеции . Метод удвоения медианы . Переход к равновеликой фигуре

Диагонали трапеции равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции.

СН=2СР = 4

S ∆C НЕ = S ∆ А C Е = S ABCD

СН = 4 ; СЕ = 5; НЕ = 3

 ∆ СНЕ - прямоугольный,  СНЕ = 90°

S ABCD = S ∆ А C Е = S ∆ СНЕ = ½ СН ·НЕ = ½·4 · 3 = 6

Ответ: 6

Метод площадей

Идея метода : площади фигуры находим, используя различные формулы или различные отрезки и углы. Приравняв эти выражения, получаем уравнение, содержащее известные и искомые величины.

Метод площадей

Медиана BM треугольника ABC равна его высоте AH. Найдите угол MBC.

Пусть  МВС = α

Т.к. ВМ - медиана

Т. к. АН = ВМ, то

  МВС = α = 30° или  МВС = 150°

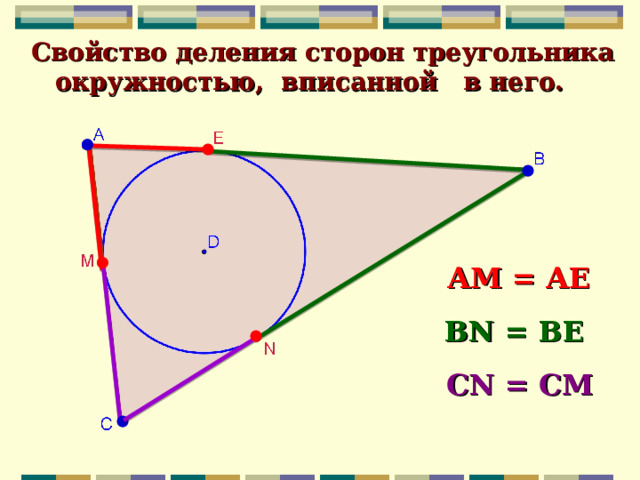
Свойство деления сторон треугольника

окружностью, вписанной в него.

АМ = АЕ

BN = B Е

CN = CM

Метод площадей

В треугольник вписана окружность радиуса 4. Одна из сторон треугольника разделена точкой касания на части, равные 6 и 8. Найдите две другие стороны треугольника.

Обозначим AM  =  AN  =  x

S ‍ △ ABC =  (8 + 6 +  x ) · 4 = (14 +  x ) · 4.

С другой стороны, по формуле Герона

х = 7

AC  =  x  + 6 = 13,

AB  =  x  + 8 = 15

Ответ: 13; 15

Метод решения: Введение вспомогательной окружности

Идея метода : ввести в рассмотрение окружность, если это возможно в данной конфигурации, чтобы применить разнообразные свойства отрезков и углов, связанных с ней

Введение вспомогательной окружности

В выпуклом четырехугольнике ABCD ∠ BCA = 20º, ∠ BAC = 35º, ∠ BDС = 70º, ∠ BDA = 40º. Найдите углы между диагоналями этого четырехугольника.

20º = ½ · 40º

∠ BCA и ∠ B D A опираются на отрезок ВА и лежат от него по одну сторону 

Можно построить окружность с центром в точке D , проходящую через остальные три вершины четырехугольника С; В и D

Введение вспомогательной окружности

В выпуклом четырехугольнике ABCD ∠ BCA = 20º, ∠ BAC = 35º, ∠ BDС = 70º, ∠ BDA = 40º. Найдите углы между диагоналями этого четырехугольника .

CD = DA как радиусы одной окружности

 ∆ ACD - равнобедренный

∠ СAD = ∠ DСA =

= (180º – 40º – 70º ) : 2 = 35º.

Из Δ APD

∠ APD = 180º – 40º – 35º = 105º .

Углы между диагоналями равны

105º и 75º

Ответ: 105°; 75°

Рекомендации учащимся при решении геометрических задач

О чертеже

• Хороший чертеж – помощник
• Все, что «увидено», должно быть обосновано
• Соблюдай пропорции и соотношения
• Используй выносные чертежи