Проект Тригонометрические функции

Тригонометрические функции .

Цель: подробно познакомится с тригонометрическими функциями, их историей и выдающимся математиком Леонардом Эйлером.

План:

1)О происхождении тригонометрии

2)Об углах

3)О графиках и таблицах

4)Синус, косинус, тангенс.

5)Формулы приведения

6)Л. Эйлер

7)Библиография

Составитель: Котов Алексей 10 класс 2018 год

Введение. Краткий обзор развития геометрии

• Первые геометрические понятия возникли в доисторические времена. Разные формы материальных тел наблюдал человек в природе: формы растений и животных, гор и извилин рек, круга и серпа Луны и т.п. Однако человек не только пассивно наблюдал природу, но практически осваивал и использовал её богатства. В процессе практической деятельности он накапливал геометрические сведения. Материальные потребности побуждали людей изготовлять орудия труда, обтёсывать камни и строить жилища, лепить глиняную посуду и натягивать тетиву на лук. Конечно, десятки и сотни тысяч раз натягивали люди свои луки, изготовляли разные предметы с прямыми рёбрами и т.п., пока постепенно дошли до понятия прямой линии. Примерно то же можно сказать о других основных геометрических понятиях. Практическая деятельность человека служила основой длительного процесса выработки отвлечённых понятий, открытия простейших геометрических зависимостей и соотношений.

Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилась потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука.

О происхождении тригонометрии.

Слово «тригонометрия» означает измерение треугольников. Возникновение тригонометрии связано с развитием астрономии- науки о движении небесных тел, о строении и развитии Вселенной - и географии.

Зачатки тригонометрии обнаружены в сохранившихся документах Древнего Вавилона, где астрономия достигла значительного развития. Вавилонские учёные составили одну из первых карт звёздного неба. Они умели предсказывать солнечные и лунные затмения. Некоторые сведения тригонометрического характера встречаются и в старинных памятниках других народов древности.

Древнегреческие учёные не знали наших тригонометрических функций, вместо синуса они пользовались хордой, равной удвоенной линии синуса половинной дуги. Заметим, что греческое слово «хорде», от которого происходит наш термин «хорда», буквально означает «тетива лука». Начало учению о тригонометрических величинах было положено в Индии. Простая на первый взгляд замена хорды полухордой- синусом - открыла большие перспективы в развитии теории тригонометрических функций. Кроме линий синуса DB и косинуса О D индийские астрономы ввели ещё одну величину: обращённый синус D А - разность между радиусом окружности и её косинусом. Сегодня мы бы записали: sin vers a= 1- cos a . Первые немногочисленные дошедшие до нас индийские произведения астрономо-тригонометрического содержания: названные «сидханты» (науки), относятся к 4-5 векам. В них уже встречаются синус, косинус и синус-версус. Индийские учёные рассматривали эти величины только для острого угла. Их вычисления сводились к рассмотрению лишь прямоугольных треугольников. Для этой цели они обычно разбивали косоугольные треугольники на ряд прямоугольных. Они знали и применяли некоторые зависимости между тригонометрическими величинами, в том числе простейшие соотношения: sin²a+cos²a=1 sin a=cos(90- а ) и др . Лишь учёные стран Среднего и Ближнего Востока ввели новые тригонометрические функции и с их помощью стали решать любые треугольники.

Расширение понятий угла.

• Понятие угла на протяжении веков не оставалось без изменений, оно обобщалось и расширялось под влиянием запросов практики и науки.

В «Началах» Евклида, как и в курсе школьной планиметрии, речь идёт о плоских углах, меньших развёрнутого. Такие углы вполне достаточны для построения учения о треугольниках и выпуклых многоугольниках. Но уже при рассмотрении простых невыпуклых многоугольников мы встречаемся со сверхтупыми углами, заключёнными между 180 и 360 градусами. Наблюдения явлений вращения различных тел, изготовление определённых приборов измерения и т. п. привели к идее угла как величины, меры вращения луча вокруг точки от начального его положения. Такая точка зрения позволила обобщить понятие угла. С одной стороны, стало возможным рассматривать углы, больше 360 градусов, с другой стороны, в зависимости от направления вращения стали различать положительные и отрицательные углы. Попутно и аналогично расширялось понятие дуги окружности.

• Градусная система углов, в которой за единицу принят угол, равный 1/360 части угла, соответствующего полному обороту одной стороны угла около его вершины, восходит к З-2 тысячелетиям до н. э., к периоду возникновения шестидесятеричной системы счисления в вавилонской математике.
• Шестидесятеричное градусное измерение, как и шестидесятеричные дроби, проникло далеко за пределы ассиро-вавилонского царства и получило широкое распространение в странах Азии, Северной Африки и Западной Европы. Они применялись, в частности, в астрономии и связанной с ней тригонометрии.
• Выдающийся немецкий математик и астроном 15 века Региомонтан отступил от шестидесятеричного деления радиуса и за единицу измерения линии синуса принял одну десятимиллионную часть радиуса, что позволило выражать синусы целыми числами. Аналогично поступали и многие последовавшие за ним европейские математики.
• Во время буржуазной революции конца 18 века во Франции была введена наряду с метрической системой мер и центезимальная (сотенная) система измерения углов, в которой прямой угол делился на 100 градусов, градус - на 100 минут, минута - на 100 секунд. Эта система применяется и поныне в некоторых геодезических измерениях, но всеобщего употребления пока не получила.
• В связи с возникновением и развитием теории пределов и математического анализа с целью придать многим формулам возможно более простой вид в тригонометрию ввели радианное измерение дуг и углов. Термин «радиан» происходит от латинского радиус.

Тригонометрия - автономная ветвь математики. Развитие учения о тригонометрических функциях и широкое применение их в практике подготовили почву для отделения тригонометрии от астрономии и формирования её как самостоятельной ветви математики. В Европе первым трудом, в котором тригонометрия рассматривалась как самостоятельная ветвь математики, было произведение Региомонтана «Пять книг о треугольниках всех видов», написанное в 1462-1466 гг. и содержащее всё, что было известно в то время в области тригонометрии. Основное содержание этой книги заимствовано из трудов, написанных на арабском языке. Региомонтан систематизировал вопросы тригонометрии и дал прекрасное изложение их. Он остановил и поместил в книге обстоятельные тригонометрические таблицы. Труд был напечатан лишь в 1533 г. и оказал большое влияние на дальнейшее развитие тригонометрии.

• О тригонометрических таблицах.

В древней Греции тригонометрия как часть астрономии достигла значительного развития. Древнегреческие учёные впервые поставили перед собой задачу решения прямоугольного треугольника, т.е. определения его элементов по трём данным элементам, из которых хотя бы один - сторона треугольника. Для решения этой задачи вначале составили таблицы длин хорд, соответствующих различным центральным углам круга постоянного радиуса. Первые тригонометрические таблицы хорд были составлены астрономом-математиком Гиппархом из Никеи (2 век до нашей эры) Таблицы синусов были введены индийскими астрономами, которые рассматривали и линию косинуса. Техника тригонометрических вычислений получила значительное развитие в Индии. Дальнейшего развития тригонометрические таблицы достигли в трудах учёных стран ислама, которые ввели понятие линии тангенса. В России первые тригонометрические таблицы были изданы в 1703 г. под названием «Таблицы логарифмов, синусов и тангенсов к научению мудролюбивых тщателей». В издании этих таблиц участвовал Л.Ф. Магницкий.

Первым графиком тригонометрической функции, появившемся в печати, была синусоида, помещённая в одном из произведений французского математика Жиля Персона де Роберваля. Этот график был им вычерчен в конце 30-х годов 17 века в связи с определением площади циклоиды. Вычерчивание и применение графиков функций вообще и тригонометрических в частности вошло, разумеется, в широкое употребление лишь после появления «Геометрии» Декарта и создания аналитической геометрии.

Название линия синусов встречается впервые в сочинении «Геометрический труд о линии синусов и циклоиде» (1659) французского автора Онора Фабри. Не сразу и нелегко дошли учёные до полного исследования тригонометрических функций и правильного вычерчивания их графиков. Лишь в 1670 г. крупный английский математик Джон Валлис разобрался в вопросе о знаках синуса в каждом квадранте и вычертил в своей «Механике» два полных оборота синусоиды, констатировав, что их бесчисленно много. Он начертил также график секанса, однако не совсем правильно. В 1668 г. появились «геометрические этюды» замечательного английского математика Джеймса Грегори, в которых впервые встречается часть тангенсоиды, соответствующая первому квадранту. Через два года были опубликованы «Геометрические лекции» другого крупного английского математика-Исаака Барроу (учителя И. Ньютона), в которых были помещены графики косинуса, тангенса и секанса для первого квадранта. Графики последних функций оказались далеко не точными. Вопрос о знаках тригонометрических функций во всех четырёх квадрантах, в частности тангенса, долгое время оставался неясным. Достаточно сказать, что один из математиков того времени - петербургский академик Фридрих Майер, много содействовавший усовершенствованию тригонометрии, считал синус и тангенс тупого угла положительным, а косинус и котангенс - отрицательным. Впервые вопрос был правильно изложен в 1705 г. в мемуарах Парижской академии наук Т. де Ланьи. В 1722 г. были опубликованы в одном из произведений Р. Кортеса, талантливого ученика и друга И. Ньютона, правильные графики тангенса и секанса для двух оборотов. Дальнейшее развитие тригонометрии было связано с именем Л. Эйлера.

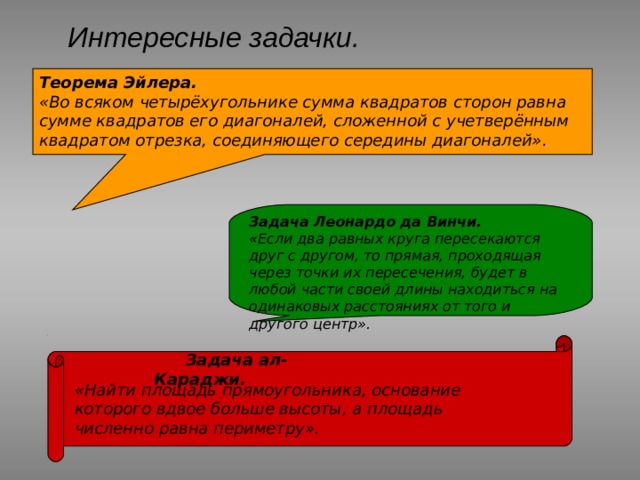
Интересные задачки.

Теорема Эйлера.

«Во всяком четырёхугольнике сумма квадратов сторон равна сумме квадратов его диагоналей, сложенной с учетверённым квадратом отрезка, соединяющего середины диагоналей».

• соединяющего середины диагоналей».

Задача Леонардо да Винчи.

«Если два равных круга пересекаются друг с другом, то прямая, проходящая через точки их пересечения, будет в любой части своей длины находиться на одинаковых расстояниях от того и другого центр».

Задача ал-Караджи.

«Найти площадь прямоугольника, основание которого вдвое больше высоты, а площадь численно равна периметру».

Леонард Эйлер. Современный вид тригонометрии. Деятельность Эйлера многогранна и разностороння. Он занимался почти всем, что интересовало в то время математиков. С.И.Вавилов Эйлер усовершенствовал как символику, так и содержание тригонометрии. Вот некоторые его заслуги: 1)Он впервые доступно изложил вопрос о знаках тригонометрических функций в каждом квадранте, установил формулы приведения, подробно исследовав области определения этих функций и обозначив их символами 2)В отличие от своих предшественников Эйлер исключил из своих формул R - целый синус, принимая R =1 и упрощая таким образом записи и вычисления. 3)Уже во «Введении в анализ бесконечных» (1748) Эйлер впервые трактует синус, косинус и т. д. не как тригонометрические линии, обязательно связанные с окружностью, а как тригонометрические функции, которые он рассматривал как отношения сторон прямоугольного треугольника, как числовые величины. 4)Понимая аргумент тригонометрической функции, не только как угол или дугу, а как любую числовую величину, Эйлер впервые стал систематически излагать тригонометрию аналитическим путём. До него каждая тригонометрическая теорема доказывалась на основании соответствующего каждому случаю геометрического чертежа. Эйлер же выводил теоремы, исходя из небольшого числа основных соотношений. 5)До Эйлера совсем редко рассматривались тригонометрические функции дуг, превышающих число пи. Лишь в его трудах разрабатывается учение о тригонометрических функциях любого аргумента.

Синус, косинус, тангенс.

• Синусом острого угла прямоугольного треугольника называется отношение противолежащего угла к гипотенузе.
• Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
• Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету

Значение синуса, косинуса и тангенса для углов 30°, 45° и 60°.

Теорема косинусов и теорема синусов. Для решения треугольника, т.е. для нахождения трёх элементов, когда известны другие три его элемента, необходимо иметь три независимых соотношения между шестью его элементами. В Евклидовой геометрии одно из них выражается равенством ے А+ ے В+ ے С=180° (1) В случае прямоугольного треугольника можно пользоваться, например, соотношением b = c • sinB (2) В случае косоугольного треугольника, помимо (1), можно использовать теорему косинусов и теорему синусов. Теорема косинусов была по существу доказана, конечно, геометрически, ещё в «Началах» Евклида. Это положение, доказанное Евклидом, эквивалентно теореме косинусов: a²=b²+c²- 2bc•cos A b²=c²+a²- 2ca•cos B c²=a²+b²- 2 ab•cos C Вместе с соотношением (1) теорема синусов, представляющая два независимых уравнения, позволяет решать любой треугольник. Теоремой синусов пользовались, начиная с 16 века и европейские математики.

Тень и рождение тангенса. Итак, понятия «тангенс» и «котангенс», как и первые таблицы этих новых тригонометрических величин, родились не из смотрения тригонометрической окружности, а из учения о солнечных часах. Ал-Хабаш ввёл и понятие «косеканс» также в связи с солнечными часами. Живший в конце 10 века в Багдаде замечательный математик Абу-л-Вафа впервые вводит в своей книге тригонометрические линии не через прямоугольный треугольник, а с помощью окружности, определяя, например, тангенс как отрезок касательной к окружности. В некоторых местах учёный принимает радиус окружности за единицу. Термины tangens (тангенс, касающийся) и secans (секанс, секущий) были введены лишь в 1583 году датским математиком Томасом Финком в связи с ролью этих линий на тригонометрической окружности. Термины «котангенс», «косеканс», образованные по аналогии с термином «косинус», встречаются впервые в 1620 году у английского учёного Эдмунта Гунтера.

Читайте, читайте Эйлера - он наш общий учитель! Крупнейшим математиком 18 века и века и одним из величайших учёных всех времён и народов был Леонард Эйлер (1707-1783). Родившись в Базеле (Швейцария) в семье пастора, Леонард получил первоначальное образование у своего отца, бывшего учеником знаменитого математика Якова Бернулли. Отец предназначал сына к богословному знанию и определил его по окончании средней школы на теологический факультет. Однако Эйлер интересовался не теологией, а математикой, и он стал слушать лекции известного профессора Иоганна Бернулли. В 19-летнем возрасте Эйлер опубликовал первую свою научную работу и принял участие в объявленном Парижской академией наук конкурсе на тему о наилучшем расположении мачт на корабле. В 1727 г. Эйлер приехал в Петербург. В Петербурге Эйлер нашёл все необходимые условия для большой научной деятельности и широкие возможности для публикации своих трудов. Здесь он женился, провёл большую часть творческого периода своей жизни, став главой первой русской математической школы, здесь он и умер. Вот почему Россия стала для Эйлера второй родиной. Он прожил в России 31 год и хорошо знал русский язык. Многие дети и внуки Эйлера остались жить в России, некоторые из его потомков поныне проживают в нашей стране.

Эйлер был всесторонне образованным учёным: знал греческий, латинский, немецкий, французский, русский и другие языки, кроме математики, физики, астрономии, имел глубочайшие знания в области географии, химии, ботанике, анатомии, медицины. Эйлер был весёлый, скромный и отзывчивый человек. Он отличался редкой трудоспособностью и был не только гениальным математиком, но и замечательным физиком, инженером, астрономом, географом и выдающимся вычислителем.

Тревожное положение в политической жизни России после смерти царевны Анны Иоанновны заставило Эйлера в1741 году переехать в Берлин. Однако учёный сохранял тесные связи с Петербургской академией наук и поддерживал переписку с М. В. Ломоносовым. В 1766 году Эйлер со своей семьёй вернулся в Петербург, где оставался и работал до последнего дня жизни.

Эйлер умер в возрасте 76 лет и был похоронен в Петербурге на Смоленском кладбище.

Труды Эйлера из области математического анализа оказали огромное влияние на развитие высшей математики. Немало было сделано и в области элементарной математики.

Библиография

• Л.С.Атанасян Геометрия
• В.И.Жохов Л.Б.Крайнева Уроки алгебры 9 класс
• Г.И.Глейзер История математики в школе