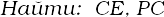| Билет № 1 | Какие углы называются смежными? Чему равна сумма смежных углов? (Сформулировать и доказать). Задача по теме ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ
| 1) | В треугольнике АВС ∠C = 600 , ∠B = 900. Высота ВВ1 равна 2 см. Найдите АВ.
| | 2) | Один из углов прямоугольного треугольника равен 600 , а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.
| | 3) | В треугольнике АВС ∠А = 900 , ∠B = 600. На стороне АС отмечена точка D так, что ∠DВC = 300, DА = 4 см. Найдите АС и расстояние от точки D до стороны ВС.
|
|
| Билет № 2 | Какие углы называются вертикальными? Каким свойством обладают вертикальные углы? (Сформулировать и доказать). Задача на построение: построить биссектрису угла
| 1) | Дан отрезок а и угол ɑ. Построить треугольник АВС, у которого АС = а, ∠А = ɑ, ∠С = 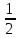 ɑ. ɑ.
| | 2) | Постройте треугольник по стороне, прилежащему к ней углу и биссектрисе треугольника, проведенной из вершины этого угла. |
|
| Билет № 3 | Какие треугольники называются равными? Сформулировать и доказать первый признак равенства треугольников. Задача по теме СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА.
| 1) | В треугольнике СDЕ точка М лежит на стороне СЕ, причем угол СМD острый. Докажите, что DЕ DМ. | | 2) | Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника. | | 3) | 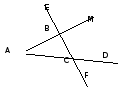
|
На рисунке 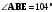 , , 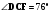 , АC = 12 см. Найдите сторону АВ треугольника АВС. , АC = 12 см. Найдите сторону АВ треугольника АВС. |
|
| Билет № 4 | Какой отрезок называется перпендикуляром, проведенным из точки А к прямой а? Сформулировать и доказать теорему о перпендикуляре, проведенном из данной точки к данной прямой. Задача по теме СУММА УГЛОВ ТРЕУГОЛЬНИКА.
| 1) | В треугольнике АВС угол А равен 500, а угол В в 12 раз меньше угла С. Найдите углы В и С.
| | 2) | В треугольнике АВС угол С равен 900, а угол В равен 350, СД - высота. Найдите углы треугольника АСД.
| | 3) | В прямоугольном треугольнике АВС (угол С равен 900) биссектрисы СД и АЕ пересекаются в точке О. ∠АОС = 1050. Найдите острые углы треугольника АВС.
| | 4) | В треугольнике АВС угол А меньше угла В в 3 раза, а внешний угол при вершине А больше внешнего угла при вершине В на 400. Найдите внутренние углы треугольника АВС.
| | 5) | В треугольнике АВС угол С равен 900, а угол В равен 700. На катете АС отложен отрезок СД, равный СВ. Найдите углы треугольника АВД.
|
|
| Билет № 5 | Какой треугольник называется равнобедренным? Как называются стороны равнобедренного треугольника? Сформулировать и доказать теорему об углах при основании равнобедренного треугольника. Задача по теме ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.
| 1) | 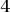
| 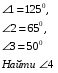
| | 2) | 
| Прямые а и b параллельны. Найдите неизвестные углы, если сумма двух накрест лежащих углов равна 1000.
| | 3) | 
| Прямые а и b параллельны. Найдите неизвестные углы, если сумма двух соответствен-ных углов равна 2600. |
|
| Билет № 6 | Какой отрезок называется биссектрисой треугольника? Доказать теорему о биссектрисе равнобедренного треугольника. Задача на построение: построить прямую, проходящую через данную точку и перпендикулярную к данной прямой.
| 1) | Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите высоту ВВ1 к боковой стороне АС.
| | 2) | Постройте прямоугольный треугольник по двум катетам.
| | 3) | Постройте прямоугольный треугольник по катету и гипотенузе. |
|
| Билет № 7 | Какие прямые называются параллельными? Сформулировать признаки параллельности прямых. Доказать один из них. Задача по теме ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ
|
| Билет № 8 | Сформулировать аксиому параллельных. Каким свойством обладают две прямые, параллельные третьей прямой? (Сформулировать и доказать). Задача по теме МЕДИАНЫ, ВЫСОТЫ и БИССЕКТРИСЫ.
| 1) | Медиана АД треугольника АВС продолжена за сторону ВС на отрезок ДЕ, равный АД, и точка Е соединена с точкой С. Найдите угол АСЕ, если ∠ АСД = 560, ∠АВД = 400.
| | 2) | В равнобедренном треугольнике АВС с основанием ВС проведена медиана АМ. Найдите медиану АМ, если периметр треугольника АВС равен 32 см, а периметр треугольника АВМ равен 24 см.
| | 3) | Докажите, сто если медиана треугольника совпадает с его высотой, то треугольник равнобедренный.
| | 4) | В равнобедренном треугольнике ДЕК с основанием ДК = 16 см отрезок EF - биссектриса. Найдите КF и ∠ЕFД. |
|
| Билет № 9 | Какая теорема называется обратной данной? Доказать, что при пересечении двух параллельных прямых секущей, накрест лежащие углы равны. Задача по теме СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
| 1) | Сумма вертикальных углов AOB и COD, образованных при пересечении прямых AD и BC, равна 108о. Найдите угол BОD.
| | 2) | С помощью транспортира начертите угол, равный 132о, и проведите биссектрису одного из смежных с ним углов.
| | 3) | Разность двух углов, образовавшихся при пересечении двух прямых, равна 420. Найдите все образовавшиеся углы.
| | 4) | Сумма трех углов, образовавшихся при пересечении двух прямых, равна 2250. Найдите все образовавшиеся углы.
| | 5) | Прямые АВ и СД пересекаются в точке О. ОК - биссектриса угла АОД, ∠СОК = 1180, Найдите ∠ВОД. |
|
| Билет № 10 | Доказать теорему о сумме углов треугольника. Задача на построение: построить треугольник по трем сторонам.
| 1) | Постройте треугольник по двум сторонам и медиане, проведенной к одной из них | | 2) | Постройте равнобедренный треугольник по основанию и боковой стороне. |
|
| Билет № 11 | Докажите, что все точки каждой из двух параллельных прямых равноудалены от другой прямой. Что называется расстоянием между двумя параллельными прямыми? Задача по теме ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ
| 1) | В треугольнике АВС ∠C = 900 , высота СС1 равна 5 см. ВС = 10 см. Найдите ∠САВ.
| | 2) | Один из углов прямоугольного треугольника равен 600 , а разность гипотенузы и меньшего катета равна 15 см. Найдите гипотенузу. | | 3) | В треугольнике АВС ∠С = 600. На стороне АС отмечена точка D так, что ∠ВDC = 600, ∠АВD = 300, СD = 5 см. Найдите АС и расстояние от точки D до стороны АВ.
|
|
| Билет № 12 | Докажите, что в треугольнике против большей стороны лежит и больший угол, и наоборот, против большего угла лежит и большая сторона Задача на построение: построить середину отрезка.
| 1) | Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС.
| | 2) | Постройте равнобедренный треугольник по основанию и медиане, проведенной к основанию. |
|
| Билет № 13 | Доказать, что в треугольнике каждая сторона меньше суммы двух других сторон. Задача по теме СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
| 1) | Внешние углы при вершинах А и В треугольника АВС равны 1250 и 1150. Какая из сторон треугольника является наибольшей? | | 2) | Две стороны треугольника равны 1,7 см и 0,6 см, а длина третьей стороны в сантиметрах выражается целым числом. Найдите третью сторону. | | 3) | В треугольнике АВС на рисунке 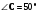 , биссектрисы углов А и В пересекаются в точке М. Найдите угол АМВ. , биссектрисы углов А и В пересекаются в точке М. Найдите угол АМВ. 
|
|
| Билет № 14 | Каким свойством обладает катет, лежащий против угла в 300? Задача по теме СУММА УГЛОВ ТРЕУГОЛЬНИКА
| 1) | В треугольнике АВС угол С равен 900, а угол А равен 700, СД - биссектриса. Найдите углы треугольника ВСД.
| | 2) | В прямоугольном треугольнике АВС (угол С равен 900) биссектрисы СД и ВЕ пересекаются в точке О. ےВОС = 950. Найдите острые углы треугольника АВС.
| | 3) | В треугольнике АВС угол А меньше угла В на 800, а внешний угол при вершине А больше внешнего угла при вершине В в 2 раза. Найдите внутренние углы треугольника АВС.
| | 4) | В треугольнике АВС угол С равен 900, а угол В равен 700. На луче СВ отложен отрезок СД, равный СА. Найдите углы треугольника АВД.
|
|
| Билет № 15 | Каким свойством обладает катет прямоугольного треугольника, если он равен половине гипотенузы. Задача по теме ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ
| 1) | 
| У фигуры, изображённой на рисунке, стороны КМ и КN равны, а также равны углы РКМ и РКN. Доказать равенство треугольников КМQ и KNQ?
| | 2) | В треугольнике АВС, изображенном на рисунке, стороны АВ и ВС равны. Известно, что АD = DC, 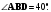 Найдите углы АВС и АDЕ. Найдите углы АВС и АDЕ. ![]() 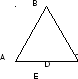
| | 3) | На рисунке АD = BC, АD ǁ BC, Доказать равенство треугольников АВС и АDС?

|
|
| Билет № 16 | Сформулируйте признаки равенства прямоугольных треугольников. Докажите один из них. Задача по теме ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
| 1) | Отрезки EF и PQ пересекаются в их середине М. Докажите, что РЕ║QF.
| | 2) | 
|
Дано: а || b, c - секущая, ∠1 - ∠2 = 1020. Найти: все образовавшиеся углы
| | 3) | 
|
Дано: ∠1=∠2, ∠3=1400. Найти: ∠4
| | 4) | 
|
Дано: АВ║СD Найдите угол АЕС.
| | 5) | Отрезок АК - биссектриса треугольника САЕ. Через точку К проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найти углы треугольника АKN, если ےCAE=780.
| | 6) | Отрезок АD - биссектриса треугольника АВС. Через точку D проведена прямая, пересекающая сторону АВ в точке Е так, что АЕ = ЕD. Докажите, что ЕD ǁАС.
|
|
| Билет № 17 | Какой угол называется внешним углом треугольника? Доказать, что внешний угол равен сумме двух внутренних углов треугольника, не смежных с ним. Задача на построение: построить треугольник по двум сторонам и углу между ними.
| 1) | Постройте треугольник по стороне, медиане, проведенной к одной из двух других сторон, и углу между данными стороной и медианой. | | 2) | Постройте равнобедренный треугольник по боковой стороне и углу между боковыми сторонами |
|
| Билет № 18 | Какой отрезок называется наклонной, проведенной из данной точки к данной прямой. Доказать, что перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из этой же точки к данной прямой. Задача по теме СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
|
| Билет № 19 | Докажите, что все точки плоскости, расположенные по одну сторону от прямой и равноудаленные от неё, лежат на прямой, параллельной данной. Задача по теме ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
| 1) |
| | 2) |

| | 3) |
| | 4) |
| | 5) |
|
|
| Билет № 20 | Докажите, что если в треугольнике два угла равны, то он равнобедренный. Задача на построение: построить треугольник по стороне и двум прилежащим к ней углам.
| 1) | Постройте равнобедренный треугольник по основанию и углу, прилежащему к основанию. | | 2) | Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу. |
|
| Дополни-тельные вопросы | Какой отрезок называется медианой треугольника? Какой отрезок называется высотой треугольника? Какой треугольник называется равносторонним? Какой треугольник называется остроугольным, тупоугольным, прямоугольным? Как называются стороны прямоугольного треугольника? Сформулировать второй признак равенства треугольников. Сформулировать третий признак равенства треугольников. Каким свойством обладают соответственные углы, образованные при пересечении двух параллельных прямых секущей? Каким свойством обладают односторонние углы, образованные при пересечении двух параллельных прямых секущей? Чему равна сумма острых углов прямоугольного треугольника? Каким свойством обладает медиана прямоугольного треугольника, проведенная к гипотенузе. Что такое теорема? Что такое аксиома ? Дайте определение окружности. Что такое центр, радиус, диаметр и хорда окружности? Как построить угол, равный данному? |







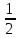 ɑ.
ɑ.
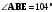 ,
, 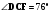 , АC = 12 см. Найдите сторону АВ треугольника АВС.
, АC = 12 см. Найдите сторону АВ треугольника АВС.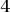
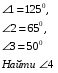

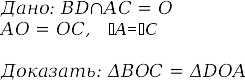
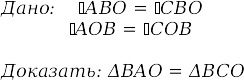
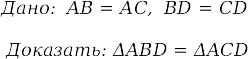
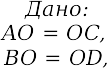
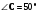 , биссектрисы углов А и В пересекаются в точке М. Найдите угол АМВ.
, биссектрисы углов А и В пересекаются в точке М. Найдите угол АМВ.

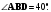 Найдите углы АВС и АDЕ.
Найдите углы АВС и АDЕ.