Алгебра 8 класс
Рабочая программа по алгебре разработана на основе требований к результатам освоения основной образовательной программы с учётом основных направлений программ, включённых в структуру основной образовательной программы школы-интерната.
Планируемые результаты освоения учебного предмета
личностные:
-
развитие способности к абстрактному мышлению;
-
развитие интереса к математическому творчеству и математических способностей;
-
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
-
формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
-
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
-
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
метапредметные:
-
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
-
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
-
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
предметные:
-
овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
-
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
В результате изучения курса алгебры 8 класса ученик научится:
-
Составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
Выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
Применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
-
Решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
-
Решать линейные и квадратные неравенства с одной переменной и их системы;
-
Решать текстовые задача алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
-
Изображать числа точками на координатной прямой;
-
Определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
-
Распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
-
Находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
-
Определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
-
Описывать свойства изученных функций, строить их графики
-
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
Выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
-
Моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
-
Описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
-
Интерпретации графиков реальных зависимостей между величинами.
В ходе освоения курса учащиеся получат возможность:
-
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
-
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
-
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
-
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
-
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
-
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
-
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Содержание учебного предмета
1. Функции и графики.
Числовые неравенства. Множества чисел. Функция, график функции. Функции у = х, у = х2, у= 1/х , их свойства и графики.
Основная цель — ввести понятия функции и ее графика, изучить свойства простейших функций и их графики.
В данной теме рассматриваются свойства числовых неравенств, изображение числовых промежутков на координатной оси, вводятся понятия функции и ее графика, показываются примеры простейших функций, их свойства и графики. При доказательстве свойств функций используются свойства неравенств. На интуитивной основе вводятся понятия непрерывности функции и графика функции, играющие важную роль при доказательстве существования квадратного корня из положительного числа.
2. Квадратные корни.
Квадратный корень. Арифметический квадратный корень. Приближенное вычисление квадратных корней. Свойства арифметических квадратных корней. Преобразование выражений, содержащих квадратные корни.
Основная цель — освоить понятия квадратного корня и арифметического квадратного корня; выработать умение преобразовывать выражения, содержащие квадратные корни.
Существование квадратного корня из положительного числа показывается с опорой на непрерывность графика функции у = х2. Подчеркивается разница между словесным определением квадратного корня из неотрицательного числа а и обозначением 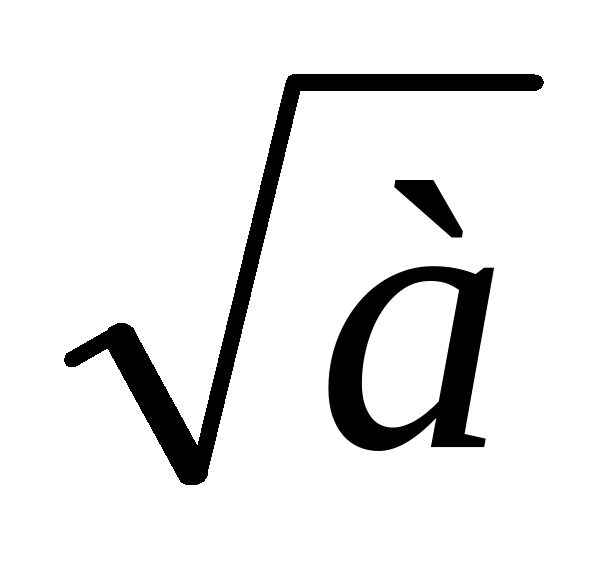 : по определению есть два квадратных корня из положительного числа а и только тот из них, который положителен, обозначается
: по определению есть два квадратных корня из положительного числа а и только тот из них, который положителен, обозначается 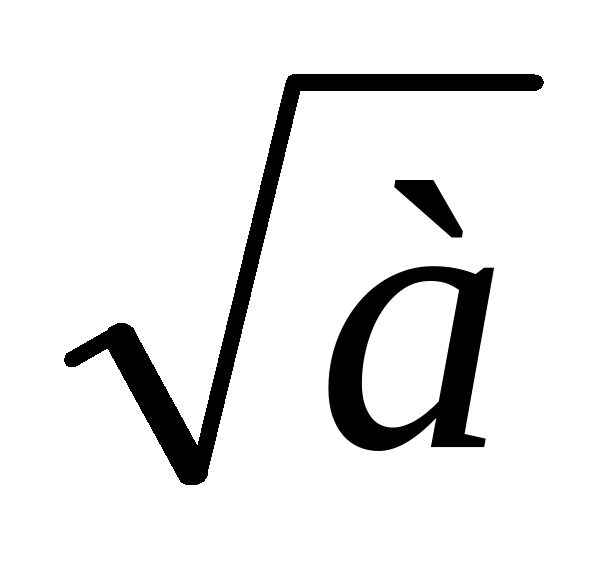 , другой обозначается -
, другой обозначается -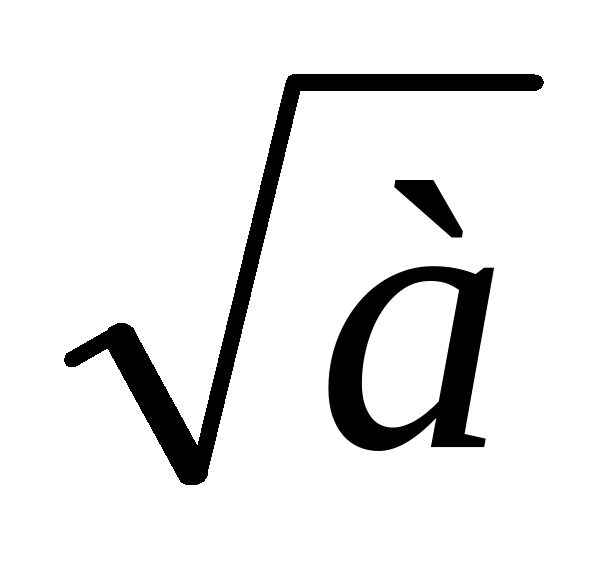 .
.
Далее доказывается иррациональность квадратного корня из любого числа, не являющегося квадратом натурального числа. Основное внимание уделяется изучению свойств квадратных корней и их использованию для преобразования выражений, содержащих квадратные корни. Учащиеся должны освоить вынесение множителя из-под знака корня, внесение множителя под знак корня и освобождение дроби от иррациональности в знаменателе в простых случаях.
3. Квадратные уравнения.
Квадратный трехчлен. Квадратное уравнение. Теорема Виета. Применение квадратных уравнений к решению задач.
Основная цель — выработать умения решать квадратные уравнения и задачи, сводящиеся к квадратным уравнениям.
В начале темы рассматривается квадратный трехчлен, выясняются условия, при которых его можно разложить на два одинаковых или на два разных множителя. На этой основе вводится понятие квадратного уравнения и его корня, рассматриваются способы решения неполного квадратного уравнения, квадратного уравнения общего вида, приведенного квадратного уравнения. Доказываются теоремы Виета (прямая и обратная), показывается применение квадратных уравнений для решения задач.
Применение квадратного уравнения существенно расширяет круг текстовых задач, которые можно предложить учащимся, дает хорошую возможность для обсуждения некоторых общих идей, связанных с их решением.
4. Рациональные уравнения.
Рациональное уравнение. Биквадратное уравнение. Распадающееся уравнение. Уравнение, одна часть которого — алгебраическая дробь, а другая равна нулю. Решение рациональных уравнений заменой неизвестных. Решение задач при помощи рациональных уравнений.
Основная цель — выработать умения решать рациональные уравнения и использовать их для решения текстовых задач.
Вводится понятие рационального уравнения, рассматриваются наиболее часто используемые виды рациональных уравнений: биквадратное, распадающееся (одна часть уравнения — произведение нескольких множителей, зависящих от х, а другая равна нулю), уравнение, одна часть которого — алгебраическая дробь, а другая равна нулю; показывается применение рациональных уравнений для решения текстовых задач.
При решении рациональных уравнений, содержащих алгебраическую дробь, обращается внимание на то, что уравнение не умножается на выражение с неизвестным, а преобразуется к уравнению, одна часть которого — алгебраическая дробь, а другая равна нулю. Идея решения рациональных уравнений заменой неизвестных показывается на примере биквадратных уравнений.
5. Линейная функция.
Прямая пропорциональная зависимость, график функции у = kх. Линейная функция и ее график. Равномерное движение. [Функции у = | х |,
у = [х], у = {х) и их графики.]
Основная цель — ввести понятия прямой пропорциональной зависимости (функции у = kx) и линейной функции; выработать умение решать задачи, связанные с графиками этих функций.
В данной теме расширяется круг изучаемых функций, появляется новая идея построения графиков — с помощью переноса. Сначала изучается частный случай линейной функции — прямая пропорциональная зависимость, исследуется расположение прямой в зависимости от углового коэффициента, решаются традиционные задачи, связанные с принадлежностью графику заданных точек, знаком функции и т. п. Затем вводится понятие линейной функции, показывается, как можно получить график линейной функции из соответствующего графика прямой пропорциональности. При этом показывается перенос графика по осям Ох и Оу. Однако основным способом построения графика линейной функции остается построение прямой по двум точкам.
Рассмотрение графиков прямолинейного движения позволяет перейти к примерам кусочно-заданных функций, способствует упрочению межпредметных связей между математикой и физикой.
Рекомендуется рассмотреть функцию у = |х|, переносы ее графика по осям координат для подготовки учащихся к изучению следующей темы.
6. Квадратичная функция.
Квадратичная функция и ее график. Уравнение прямой. Уравнение окружности. Построение графиков функций, содержащих модули.
Основная цель — изучить квадратичную функцию и ее график; выработать умение решать задачи, связанные с графиком квадратичной функции.
В начале темы рассматривается функция у= ах2(сначала для а 0, потом для а≠ 0) и формулируются ее свойства, тут же иллюстрируемые на графиках. Обращается внимание, что график функции у= а (х - х0)2 + у0получается переносом графика функции у = ах2, что показывает взаимосвязь между частным и общим случаями квадратичной функции. Большое внимание уделяется построению графика квадратичной функции по точкам с вычислением абсциссы вершины параболы.
Рассмотрение графика движения тела в поле притяжения Земли дает еще один пример межпредметных связей между математикой и физикой, позволяет показать применение изучаемого материала на примере задач с физическим содержанием.
7. Системы рациональных уравнений.
Системы рациональных уравнений. Системы уравнений первой и второй степени. Решение задач при помощи систем уравнений первой и второй степени, систем рациональных уравнений.
Основная цель - выработать умение решать системы; уравнений первой и второй степени, системы рациональных уравнений, задачи, приводящие к таким системам.
В начале данной темы вводятся понятия системы рациональных уравнений, ее решения. Следует обратить внимание, что многие определения и приемы действий с системами уравнений известны из курса 7 класса. Поэтому изложение материала данной темы целесообразно начать с повторения темы «Системы линейных уравнений».
8. Графический способ решения систем уравнений.
Графический способ решения систем двух уравнений с двумя неизвестными и исследования системы двух уравнений первой степени с двумя неизвестными. Решение систем уравнений и уравнений графическим способом.
Основная цель — выработать умение решать системы уравнений и уравнения графическим способом.
Графический способ решения систем уравнений рассматривается сначала для двух уравнений первой степени с двумя неизвестными. После графического способа исследования системы двух уравнений первой степени с двумя неизвестными рассматриваются графический способ решения системы уравнений первой и второй степени и примеры решения уравнений графическим способом.
9. Повторение.
Тематическое планирование
| № п/п | Сроки проведения | Тема урока | Домашнее задание |
|
| по плану | факт. |
|
|
| Повторение курса 7 класса (3ч ). |
| 1. |
|
| Повторение. Действительные числа. |
|
| 2. |
|
| Повторение. Алгебраические выражения. |
|
| 3. |
|
| Повторение. Линейные уравнения. Входная контрольная работа. |
|
| Простейшие функции. Квадратные корни (25 ч). |
| Функции и графики (9 ч). |
| 4. |
|
| Числовые неравенства. |
|
| 5. |
|
| Числовые неравенства. |
|
| 6. |
|
| Координатная ось. |
|
| 7. |
|
| Множества чисел. |
|
| 8. |
|
| Множества чисел. |
|
| 9. |
|
| Декартова система координат на плоскости. |
|
| 10. |
|
| Понятие функции. |
|
| 11. |
|
| Понятие функции. |
|
| 12. |
|
| Понятие графика функции. |
|
| Функции у = х, у = x2, y =1/x (7 ч). |
| 13. |
|
| Функция y = x и ее график. |
|
| 14. |
|
| Функция y = x и ее график. |
|
| 15. |
|
| Функция y = x^2 . |
|
| 16. |
|
| График функции y = x^2 . |
|
| 17. |
|
| Функция y = 1/x. |
|
| 18. |
|
| График функции y = 1/x. |
|
| 19. |
|
| Контрольная работа № 1 «Простейшие функции». |
|
| Квадратные корни (9 ч) |
| 20. |
|
| Анализ контрольной работы. Понятие квадратного корня. |
|
| 21. |
|
| Понятие квадратного корня. |
|
| 22. |
|
| Арифметический квадратный корень. |
|
| 23. |
|
| Арифметический квадратный корень. |
|
| 24. |
|
| Свойства арифметических квадратных корней. |
|
| 25. |
|
| Свойства арифметических квадратных корней. |
|
| 26. |
|
| Свойства арифметических квадратных корней. |
|
| 27. |
|
| Квадратный корень из натурального числа. |
|
| 28. |
|
| Контрольная работа № 2 «Квадратные корни». |
|
| Квадратные и рациональные уравнения (29 ч). |
| Квадратные уравнения (16 ч) |
| 29. |
|
| Анализ контрольной работы. Квадратный трехчлен. |
|
| 30. |
|
| Квадратный трехчлен. |
|
| 31. |
|
| Понятие квадратного уравнения. |
|
| 32. |
|
| Понятие квадратного уравнения. |
|
| 33. |
|
| Неполное квадратное уравнение. |
|
| 34. |
|
| Неполное квадратное уравнение. |
|
| 35. |
|
| Решение квадратного уравнения общего вида. |
|
| 36. |
|
| Решение квадратного уравнения общего вида. |
|
| 37. |
|
| Решение квадратного уравнения общего вида. |
|
| 38. |
|
| Приведенное квадратное уравнение. |
|
| 39. |
|
| Приведенное квадратное уравнение. |
|
| 40. |
|
| Теорема Виета. |
|
| 41. |
|
| Теорема Виета. |
|
| 42. |
|
| Применение квадратных уравнений к решению задач. |
|
| 43. |
|
| Применение квадратных уравнений к решению задач. |
|
| 44. |
|
| Контрольная работа № 3 «Квадратные уравнения». |
|
| Рациональные уравнения (13 ч). |
| 45. |
|
| Анализ контрольной работы. Понятие рационального уравнения. |
|
| 46. |
|
| Биквадратное уравнение. |
|
| 47. |
|
| Биквадратное уравнение. |
|
| 48. |
|
| Распадающееся уравнение. |
|
| 49. |
|
| Распадающееся уравнение. |
|
| 50. |
|
| Уравнение, одна часть которого алгебраическая дробь, а другая – нуль. |
|
| 51. |
|
| Уравнение, одна часть которого алгебраическая дробь, а другая – нуль. |
|
| 52. |
|
| Уравнение, одна часть которого алгебраическая дробь, а другая – нуль. |
|
| 53. |
|
| Решение рациональных уравнений. |
|
| 54. |
|
| Решение рациональных уравнений. |
|
| 55. |
|
| Решение задач при помощи рациональных уравнений. |
|
| 56. |
|
| Решение задач при помощи рациональных уравнений. |
|
| 57. |
|
| Контрольная работа № 4 «Рациональные уравнения». |
|
| Линейная, квадратичная и дробно – линейная функции (23 ч). |
| Линейная функция (9 ч). |
| 58. |
|
| Анализ контрольной работы. Прямая пропорциональность. |
|
| 59. |
|
| Прямая пропорциональность. |
|
| 60. |
|
| График функции y = kx. |
|
| 61. |
|
| График функции y = kx. |
|
| 62. |
|
| Линейная функция и ее график. |
|
| 63. |
|
| Линейная функция и ее график. |
|
| 64. |
|
| Линейная функция и ее график. |
|
| 65. |
|
| Равномерное движение. |
|
| 66. |
|
| Функция y = |x| и ее график. |
|
| Квадратичная функция (9 ч). |
| 67. |
|
| Функция y = x^2 (a 0). |
|
| 68. |
|
| Функция y = x^2 (a 0). |
|
| 69. |
|
| Функция y = x^2 (a ≠0). |
|
| 70. |
|
| Функция y = x^2 (a ≠ 0). |
|
| 71 |
|
| График функции y = a(x – x0)^2 + y0. |
|
| 72. |
|
| График функции y = a(x – x0)^2 + y0. |
|
| 73. |
|
| График функции y = a(x – x0)^2 + y0. |
|
| 74. |
|
| Квадратичная функция и ее график. |
|
| 75. |
|
| Квадратичная функция и ее график. |
|
| Дробно – линейная функция (5 ч). |
| 76. |
|
| Обратная пропорциональность. |
|
| 77. |
|
| Функция y = k/x ( k0). |
|
| 78. |
|
| Функция y = k/x ( k≠0). |
|
| 79 |
|
| Дробно – линейная функция и ее график. |
|
| 80 |
|
| Контрольная работа № 5 « Линейная , квадратичная и дробно – линейная функции». |
|
| Системы рациональных уравнений (16 ч). |
| Системы рациональных уравнений (8 ч). |
| 81. |
|
| Анализ контрольной работы. Понятие системы рациональных уравнений. |
|
| 82. |
|
| Понятие системы рациональных уравнений. |
|
| 83. |
|
| Решение систем рациональных уравнений способом подстановки. |
|
| 84. |
|
| Решение систем рациональных уравнений способом подстановки. |
|
| 85. |
|
| Решение систем рациональных уравнений другими способами. |
|
| 86. |
|
| Решение систем рациональных уравнений другими способами. |
|
| 87. |
|
| Решение задач при помощи систем рациональных уравнений. |
|
| 88. |
|
| Решение задач при помощи систем рациональных уравнений. |
|
| Графический способ решения систем уравнений (8 ч). |
| 89. |
|
| Графический способ решения систем двух уравнений первой степени с двумя неизвестными. |
|
| 90. |
|
| Графический способ решения систем двух уравнений первой степени с двумя неизвестными. |
|
| 91. |
|
| Решение систем уравнений графическим способом. |
|
| 92. |
|
| Решение систем уравнений графическим способом. |
|
| 93. |
|
| Примеры решения уравнений графическим способом. |
|
| 94. |
|
| Примеры решения уравнений графическим способом. |
|
| 95. |
|
| Контрольная работа № 6 «Системы рациональных уравнений». |
|
| 96 |
|
| Анализ контрольной работы. Графики и функции. |
|
| Повторение (9 ч) |
| 97. |
|
| Квадратные корни. |
|
| 98. |
|
| Квадратные уравнения. |
|
| 99. |
|
| Рациональные уравнения. |
|
| 100. |
|
| Системы рациональных уравнений и способы их решений. |
|
| 101. |
|
| Системы рациональных уравнений и способы их решений. |
|
| 102. |
|
| Итоговая контрольная работа. |
|
| 103. |
|
| Решение тренировочных задач. |
|
| 104. |
|
| Решение тренировочных задач. |
|
| 105. |
|
| Решение тренировочных задач. |
|


























