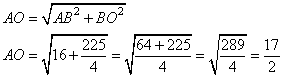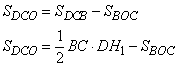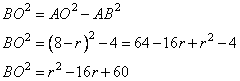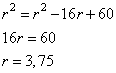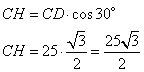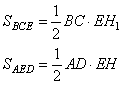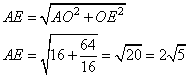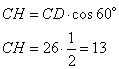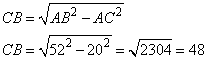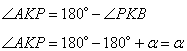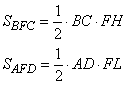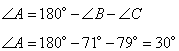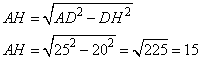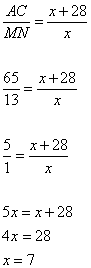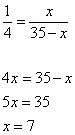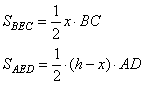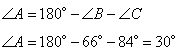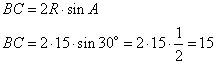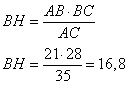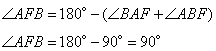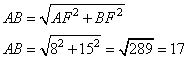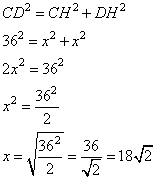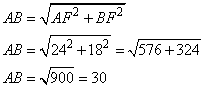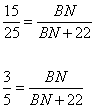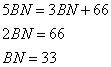Разбор задач ОГЭ по геометрии (2 часть)

1.Задание 24. Окружность с центром на стороне АС треугольника ABC проходит через вершину С и касается прямой АВ в точке В. Найдите АС, если диаметр окружности равен 15, а АВ = 4.

Решение.

Сделаем построение, проведен радиус BO, который будет перпендикулярен стороне AB, так как AB – касательная к окружности по условию задачи (см. рисунок).

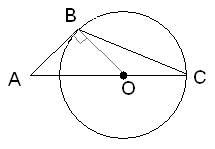
Рассмотрим прямоугольный треугольник ABO, у которого известны два катета: AB=4 и BO=d/2, где d=15 – диаметр окружности. Тогда по теореме Пифагора, длина отрезка AO равна

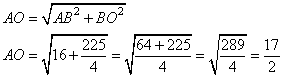
В результате получаем, что длина отрезка AC=AO+OC есть

.

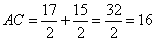Ответ: 16.

2.Задание 25. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Докажите, что площади треугольников АОВ и COD равны.

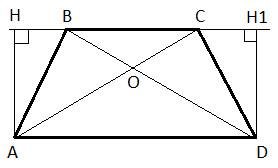
Решение.

Запишем площадь треугольника ABO в виде:

,

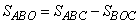где 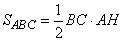  - площадь треугольника ABC;  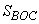 - площадь треугольника BOC. То есть площадь треугольника ABO можно представить как:

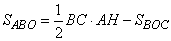.  (1)

Аналогично запишем площадь треугольника DCO, имеем:

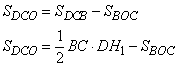
Так как 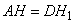 , то последнее выражение можно переписать в виде:

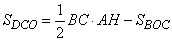.  (2)

Выражения (1) и (2) идентичны между собой и описывают площади треугольников ABO и DCO, то есть площади этих треугольников равны. Утверждение доказано.

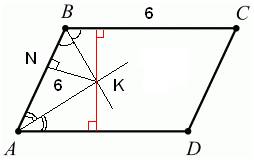
3.Задание 26. Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если ВС = 6, а расстояние от точки K до стороны АВ равно 6.

Решение.

Так как ABCD параллелограмм, а AK и BK – биссектрисы углов A и B, то точка K равноудалена от сторон AB и BC (см. рисунок). По условию задачи точка K удалена от стороны AB на расстояние 6 единиц, следовательно, от стороны BC она также удалена на 6 единиц. Получаем, что высота параллелограмма (красная линия на рисунке) равна 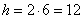  единиц. Тогда площадь параллелограмма можно найти как

.

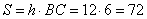Ответ: 72.

4.Задание 24. Окружность с центром на стороне АС треугольника ABC проходит через вершину С и касается прямой АВ в точке В. Найдите диаметр окружности, если АВ = 2, АС = 8.

Решение.

Сделаем построение, проведен радиус BO, который будет перпендикулярен стороне AB, так как AB – касательная к окружности по условию задачи (см. рисунок).

Введем обозначение OB=OC=r – радиусы окружности. Тогда отрезок 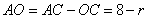 . Выразим квадрат радиуса BO=r  из прямоугольного треугольника ABO по теореме Пифагора, получим следующее выражение:

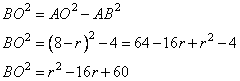
Так как BO=r, получаем уравнение:

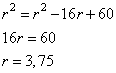
И диаметр окружности равен  .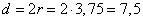

Ответ: 7,5.

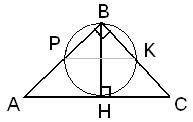
5.Задание 24. Точка Н является основанием высоты ВН, проведённой из вершины прямого угла В прямоугольного треугольника ABC. Окружность с диаметром ВН пересекает стороны АВ и СВ в точках Р и K соответственно. Найдите ВН, если РК = 11.

Решение.

Для решения данной задачи нужно вспомнить, что в любой окружности хорды, проведенные от ее диаметра, всегда пересекаются под углом в 90 градусов. Следовательно, точки P и K находятся на разных концах диаметра окружности, и так как PK=11, то и диаметр окружности равен 11. В задаче сказано, что BH – это диаметр окружности, значит, BH=PK=11.

Ответ: 11.

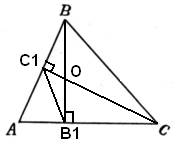
6.Задание 25. В остроугольном треугольнике ABC проведены высоты BB1 и CC1 Докажите, что углы BB1C1 и ВСC1 равны.

Решение.

1. Из рисунка видно, что треугольники BOC1 и CB1O подобны по двум углам (углы 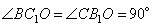 , так как CC1 и BB1 – высоты, а углы  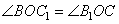 как вертикальные углы). В подобных треугольниках соответственные стороны пропорциональны, то есть можно написать соотношение

.

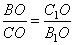2. Треугольники C1OB1 и BOC подобны по двум пропорциональным сторонам и углам между ними (углы 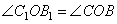  – вертикальные).

3. Из подобия треугольников следует равенство углов:

,

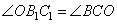а, значит, равны и углы

.

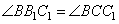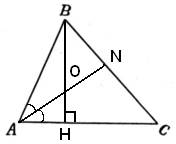
7.Задание 26. В треугольнике ABC биссектриса угла А делит высоту, проведённую из вершины В, в отношении 5 : 4, считая от точки В. Найдите радиус окружности, описанной около треугольника ABC, если ВС = 12.

Решение.

По условию задачи BO:OH=5:4, следовательно, OH:BO=4:5. По свойству биссектрисы AH:AB=HO:BO=4:5,  но AH:AB – это косинус угла A, то есть 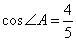 . Рассмотрим прямоугольный треугольник AHB, в котором условно катет AH=4, а гипотенуза AB=5. По теореме Пифагора находим

.

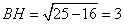Тогда синус угла A равен 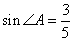 . По следствию теоремы синусов имеем:

,

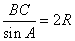где R – радиус описанной окружности. Следовательно,

.

Ответ: 10.

8.Задание 24. Точка Н является основанием высоты ВН, проведённой из вершины прямого угла В прямоугольного треугольника ABC. Окружность с диаметром ВН пересекает стороны АВ и СВ в точках Р и К соответственно. Найдите ВН, если РК = 12.

Решение.

Для решения данной задачи нужно вспомнить, что в любой окружности хорды, проведенные от ее диаметра, всегда пересекаются под углом в 90 градусов. Следовательно, точки P и K находятся на разных концах диаметра окружности, и так как PK=12, то и диаметр окружности равен 12. В задаче сказано, что BH – это диаметр окружности, значит, BH=PK=12.

Ответ: 12.

9.Задание 24. Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, a CD = 25.

Решение.

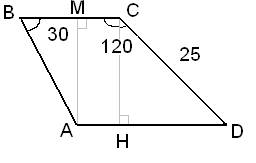
Рассмотрим прямоугольный треугольник CDH, в котором угол 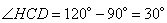 . Так как косинус угла – это отношение прилежащего катета к гипотенузе, то можно записать, что

,

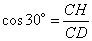откуда

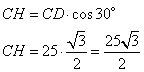
Рассмотрим прямоугольный треугольник ABM, в котором AM=CH. Известно, что синус угла – это отношение противолежащего катета к гипотенузе, то есть, имеем:

,

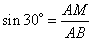откуда

.

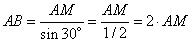Подставляя вместо AM найденное ранее числовое значение, получаем:

.

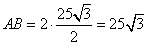Ответ: 25√3.

10.Задание 25. Точка Е — середина боковой стороны АВ трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции.

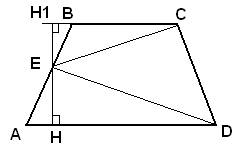
Решение.

Из рисунка видно, что площадь треугольника ECD можно выразить как

.

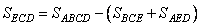Площадь трапеции можно вычислить как произведение средней линии трапеции 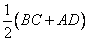  на высоту HH1, то есть

.

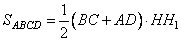Площади треугольников BCE и AED равны

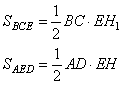
Тогда, площадь треугольника ECD равна

.

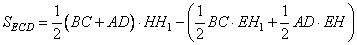Учитывая, что 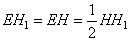 , получаем:

То есть площадь треугольника ECD равна половине площади трапеции ABCD.

11.Задание 26. В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8. Найдите стороны треугольника ABC.

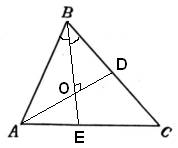
Решение.

1. По условию задачи биссектриса BE и медиана AD пересекаются под прямым углом. Следовательно, в треугольнике ABD BO – медиана, и треугольник ABD равнобедренный с основанием AD. Тогда AO=OD=4.

Если медиана с биссектрисой пересекаются под 90 градусов, то в точке пересечения биссектриса делится в отношении 3:1, считая от вершины, следовательно,  .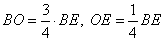

2. Рассмотрим прямоугольный треугольник AOB, в котором известны два катета AO и BO. По теореме Пифагора найдем гипотенузу AB:

.

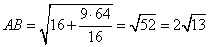Так как BD=AB, а BC=2BD=2AB, то

.

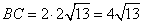3. Вычислим длину отрезка AE из прямоугольного треугольника AOE по теореме Пифагора:

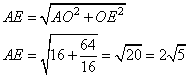
По свойству биссектрисы треугольника можно записать, что

,

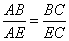откуда

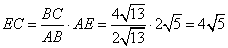
и сторона AC равна

.

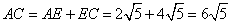Ответ:  .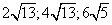

12.Задание 24. Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, a CD = 26.

Решение.

Рассмотрим прямоугольный треугольник CDH, в котором угол 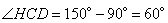 . Так как косинус угла – это отношение прилежащего катета к гипотенузе, то можно записать, что

,

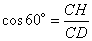откуда

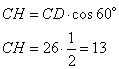
Рассмотрим прямоугольный треугольник ABM, в котором AM=CH. Известно, что синус угла – это отношение противолежащего катета к гипотенузе, то есть, имеем:

,

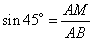откуда

.

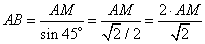Подставляя вместо AM найденное ранее числовое значение, получаем:

.

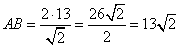Ответ: 13√2.

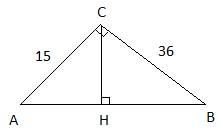
13.Задание 24. Катеты прямоугольного треугольника равны 15 и 36. Найдите высоту, проведённую к гипотенузе.

Решение.

Высоту CH можно найти из формулы площади треугольника как

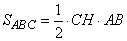,  (1)

где AB – гипотенуза прямоугольного треугольника, равная (по теореме Пифагора)

.

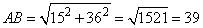Площадь прямоугольного треугольника ABC также равна половине произведения его катетов:

.

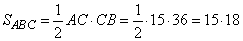Подставим все известные величины в формулу (1) и найдем высоту CH, получим:

,

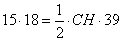откуда

.

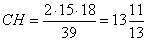Ответ:  .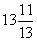

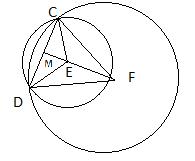
14.Задание 25. Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой CD. Докажите, что  .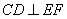

Решение.

Так как точки C и D лежат как на малой, так и на большой окружностях, то CE=ED – радиусы малой окружности, а CF=FD – радиусы большой окружности. Следовательно, треугольники CDE и CDF – равнобедренные с основанием CD. Отсюда следует, что треугольники CEF=DEF по трем сторонам. Так как в равных треугольниках углы также равны, то получаем, что  , а значит, FE – биссектриса равнобедренного треугольника CFD. Но биссектриса в равнобедренном треугольнике, проведенная к основанию, также является высотой, следовательно  .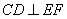

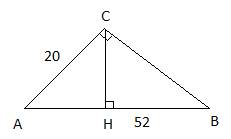
15.Задание 24. Катет и гипотенуза прямоугольного треугольника равны 20 и 52. Найдите высоту, проведённую к гипотенузе.

Решение.

Высоту CH прямоугольного треугольника ABC можно найти из формулы площади треугольника

,

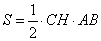откуда

.

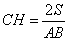Площадь прямоугольного треугольника можно найти как произведения его катетов, деленное пополам:

,

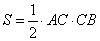где катет CB вычисляется по теореме Пифагора как

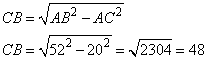
Таким образом, площадь треугольника равна

,

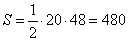и высота

.

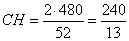Ответ:  .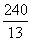

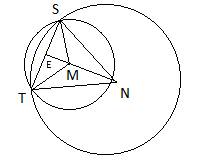
16.Задание 25. Окружности с центрами в точках М и N пересекаются в точках S и Т, причём точки М и N лежат по одну сторону от прямой ST. Докажите, что MN перпендикулярна ST.

Решение.

Так как точки S и T лежат как на малой, так и на большой окружностях, то SM=TM – радиусы малой окружности, а SN=TN – радиусы большой окружности. Следовательно, треугольники STM и STN – равнобедренные с основанием ST. Отсюда следует, что треугольники TMN=SMN по трем сторонам. Так как в равных треугольниках углы также равны, то получаем, что 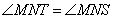 , а значит, MN – биссектриса равнобедренного треугольника SNT. Но биссектриса в равнобедренном треугольнике, проведенная к основанию, также является высотой, следовательно  .

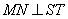17.Задание 24. Окружность пересекает стороны АВ и АС треугольника ABC в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АК = 14 , а сторона АС в 2 раза больше стороны ВС.

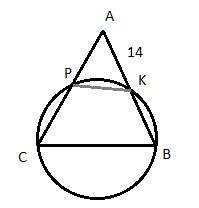
Решение.

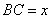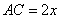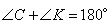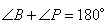Пусть сторона  , тогда  , так как она в 2 раза больше стороны BC по условию задачи. Теперь рассмотрим четырехугольник CPKB, который вписан в окружность. Как известно, у такого четырехугольника сумма противоположных углов равна 180 градусов, то есть   и  . Предположим, что угол  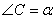, тогда угол  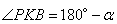, теперь, учитывая, что углы  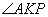 и 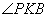  смежные, то угол

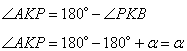
то есть он равен углу 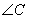 . Аналогично и для угла  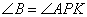. Из равенства этих двух пар углов следует, что треугольники ACB и APK подобны друг другу по двум углам.

Для подобных треугольников можно записать следующее соотношение:

,

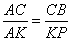откуда

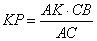
и подставляя числовые значения, имеем:

.

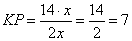Ответ: 7.

18.Задание 25. На средней линии трапеции ABCD с основаниями AD и ВС выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.

Решение.

По условию задачи точка F лежит на отрезке MN – средней линии трапеции. Проведем через эту точку высоту HL трапеции. Тогда по определению средней линии, отрезки FH=FL=1/2HL. Используя данные обозначения, выразим площади треугольников BFC и AFD следующим образом:

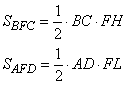
Соответственно, сумма этих площадей составит величину, равную

но так как 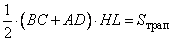  - это площадь всей трапеции, то получаем, что

.

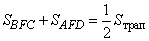Положение доказано.

19.Задание 24. Окружность пересекает стороны АВ и АС треугольника ABC в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АК = 18, а сторона АС в 1,2 раза больше стороны ВС.

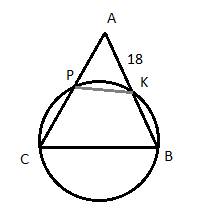
Решение.

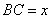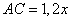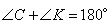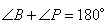Пусть сторона  , тогда  , так как она в 1,2 раза больше стороны BC по условию задачи. Теперь рассмотрим четырехугольник CPKB, который вписан в окружность. Как известно, у такого четырехугольника сумма противоположных углов равна 180 градусов, то есть   и  . Предположим, что угол  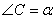, тогда угол  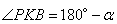, теперь, учитывая, что углы  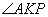 и 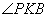  смежные, то угол

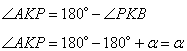
то есть он равен углу 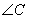 . Аналогично и для угла  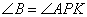. Из равенства этих двух пар углов следует, что треугольники ACB и APK подобны друг другу по двум углам.

Для подобных треугольников можно записать следующее соотношение:

,

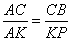откуда

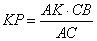
и подставляя числовые значения, имеем:

.

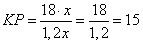Ответ: 15.

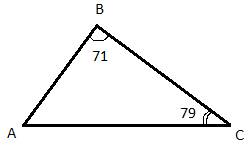
20.Задание 24. Углы В и С треугольника АБС равны соответственно 71° и 79°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 8.

Решение.

Сначала вычислим третий угол A, учитывая, что сумма всех углов в треугольнике равна 180 градусов, имеем:

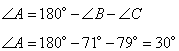
В соответствии с теоремой синусов, можно записать

,

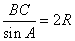где 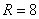  - радиус описанной вокруг треугольника окружности. Из последнего выражения имеем:

.

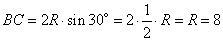Ответ: 8.

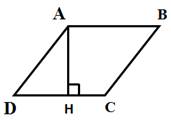
21.Задание 24. Высота АН ромба ABCD делит сторону CD на отрезки DH = 20 и СН = 5. Найдите высоту ромба.

Решение.

Длина стороны DC ромба ABCD, равна

DC=DH+HC=20+5=25.

Так как у ромба все стороны равны, то AD=DC=25. В результате, имеем прямоугольный треугольник, ADH, в котором известна гипотенуза AD и катет DH. Тогда второй катет AH (высота ромба) можно найти по теореме Пифагора:

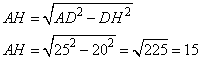
Ответ: 15.

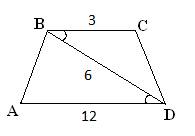
22.Задание 25. Основания ВС и AD трапеции ABCD равны соответственно 3 и 12, BD = 6. Докажите, что треугольники CBD и BDA подобны.

Решение.

Так как ABCD трапеция, то ее основания 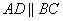 , следовательно, равны и углы  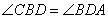 как накрест лежащие при параллельных BC, AD и секущей BD. Рассмотрим треугольники CBD и BDA, у которых имеем следующие пропорци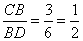и:

 и  .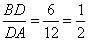

Следовательно, треугольники CBD и BDA подобны друг другу по двум пропорциональным сторонам и равным углам, заключенными между этими сторонами.

23.Задание 24. Прямая, параллельная стороне АС треугольника ABC, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 13, АС = 65, NC = 28.

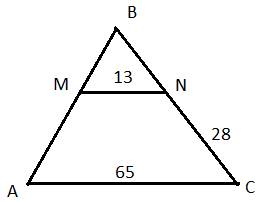
Решение.

Сначала докажем, что треугольники BMN и ABC подобные. Так как 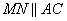 , то равны и углы  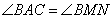 и  . Следовательно, треугольники BMN и BAC подобны по двум углам. Для подобных треугольников можно записать следующее соотношение длин их сторон:

.

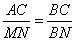Пусть сторона 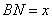 , тогда сторона  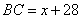 (по условию задачи), и отношение сторон можно записать как

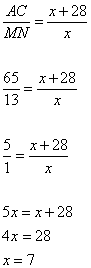
То есть длина стороны BN=7.

Ответ: 7.

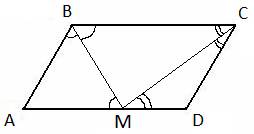
24.Задание 25. Биссектрисы углов В и С параллелограмма ABCD пересекаются в точке М стороны AD. Докажите, что М — середина AD.

Решение.

Так как ABCD – параллелограмм, то стороны 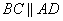  и 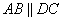 . Из этого положения следует равенство углов  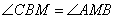 и  . Так как BM – биссектриса, то равны и углы  . Из равенства двух углов при основании BM следует, что треугольник ABM – равнобедренный, с равными сторонами AB=AM. Аналогично для треугольника CMD, у которого углы при основании MC равны, следовательно, он равнобедренный и CD=MD. Учитывая, что ABCD – параллелограмм, у которого стороны AB=CD, то автоматически следует, что и AM=MD, то есть точка M – середина отрезка AD. Положение доказано.

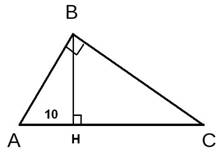
25.Задание 24. Точка Н является основанием высоты, проведённой из вершины прямого угла В треугольника ABC к гипотенузе АС. Найдите АВ, если АН = 10, АС = 40.

Решение.

В соответствии со свойством о средних пропорциональных отрезках в прямоугольном треугольнике, катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. То есть в данном случае можно записать:

,

и, подставляя числовые значения, имеем:

.

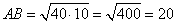Ответ: 20.

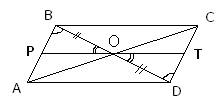
26.Задание 25. Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны АВ и CD в точках Р и Т соответственно. Докажите, что BP = DT.

Решение.

У параллелограмма диагонали BD и AC делятся в точке пересечения O пополам, то есть BO=OD. Кроме того, в параллелограмме противоположные стороны параллельны, то есть 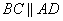  и, следовательно,  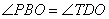 - как накрест лежащие при параллельных прямых и секущей BD. Углы   - как вертикальные углы. В результате имеем, что треугольники BOP и DOT равны по стороне и двум прилежащим к ней углам, а, следовательно, равны и стороны BP=DT.

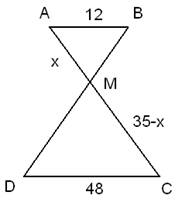
Задание 24. Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 12, DC = 48, АС = 35.

Решение.

Так как 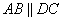 , то углы  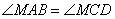 как накрест лежащие углы при параллельных прямых AB, DC и секущей AC. Углы   как вертикальные углы. Следовательно, треугольники AMB и CMD подобны по двум углам. Для подобных треугольников можно записать следующее отношение:

.

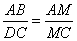Пусть AM=x, тогда MC=AC-AM=35-x, и отношение примет вид:

,

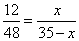откуда

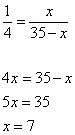
и MC=35-7=28.

Ответ: 28.

27.Задание 25. Внутри параллелограмма ABCD выбрали произвольную точку Е. Докажите, что сумма площадей треугольников ВЕС и AED равна половине площади параллелограмма.

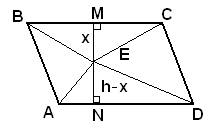
Решение.

Проведем в параллелограмме ABCD высоту MN, равную h, и проходящую через точку E. Пусть расстояние ME=x, тогда NE=h-x. Площадь параллелограмма можно вычислить как

,

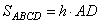а площади треугольников как

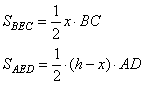
Так как в параллелограмме противоположные стороны равны, то BC=AD и сумма площадей треугольников равна

,

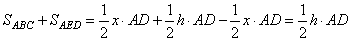что в точности равно половине площади параллелограмма ABCD. Утверждение доказано.

28.Задание 24. Углы В и С треугольника ABC равны соответственно 66° и 84°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 15.

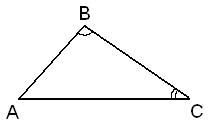
Решение.

Так как сумма углов в любом треугольнике равна 180 градусов, то угол А равен

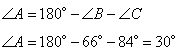
Найдем длину BC из теоремы синусов как

,

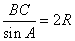где 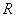  - радиус описанной окружности вокруг треугольника ABC. Отсюда получаем:

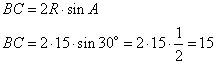
Ответ: 15.

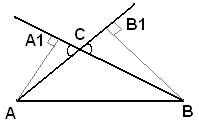
29.Задание 25. В треугольнике ABC с тупым углом АСВ проведены высоты АА1 и ВВ1. Докажите, что треугольники A1CB1 и АСВ подобны.

Решение.

Рассмотрим сначала два прямоугольных треугольника AA1C и BB1C, которые подобны по двум углам (один угол у них прямой, а углы 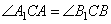  как вертикальные). У подобных треугольников AA1C и BB1C сторона A1C пропорциональна стороне B1C, а сторона AC пропорциональна стороне BC.

Рассмотрим теперь треугольники A1CB1 и ACB, у которых пропорциональны стороны AC, CB и A1C, B1C и равны углы 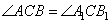 между этими сторонами как вертикальные. По второму признаку подобия два треугольника подобны, если стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника и углы, заключенные между этими сторонами, равны. То есть треугольники A1CB1 и ACB подобны друг другу. Утверждение доказано.

30.Задание 24. Катеты прямоугольного треугольника равны 21 и 28. Найдите высоту, проведённую к гипотенузе.

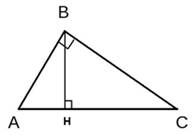
Решение.

Высоту BH можно найти из формулы площади прямоугольного треугольника 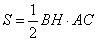 , где AC – гипотенуза прямоугольного треугольника, равная (в соответствии с теоремой Пифагора)  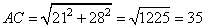. Также площадь прямоугольного треугольника равна  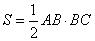. Приравнивая эти площади, получаем:

,

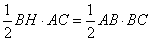откуда

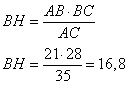
Ответ: 16,8.

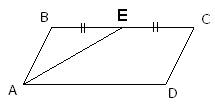
31.Задание 25. Сторона ВС параллелограмма ABCD вдвое больше стороны АВ. Точка Е — середина стороны ВС. Докажите, что АЕ — биссектриса угла BAD.

Решение.

Так как ABCD – параллелограмм, то стороны 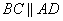 , следовательно, углы  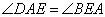 как накрест лежащие при параллельных прямых BC, AD и секущей AE. По условию задачи BC больше AB в 2 раза, и, учитывая, что E – это середина BC, то AB=BE. Таким образом, треугольник ABE – равнобедренный, с равными углами  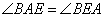 при основании AE. Но углы  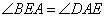, следовательно,  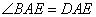, и это означает, что AE — биссектриса угла BAD. Утверждение доказано.

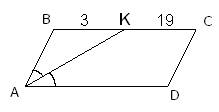
32.Задание 24. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке K. Найдите периметр параллелограмма, если ВК = 3, CK = 19.

Решение.

Так как ABCD – параллелограмм, то стороны 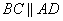 , следовательно, углы  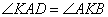 как накрест лежащие при параллельных прямых BC, AD и секущей AK. По условию задачи AK – биссектриса угла A, значит, углы  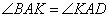 и отсюда получаем, что  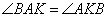. Таким образом, треугольник ABK равнобедренный со сторонами AB=BK=3 и основанием AK. Учитывая, что в параллелограмме противоположные стороны равны, и BC=3+19=22, то периметр равен

.

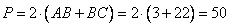Ответ: 50.

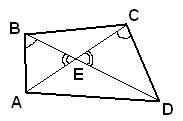
33.Задание 25. В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.

Решение.

Проведем в четырехугольнике диагонали AC и BD и отметим точку E на их пересечении. Рассмотрим треугольники ABE и DEC, у которых равны углы 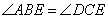  по условию задачи, а также равны углы  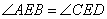 как вертикальные. Таким образом, треугольники ABE и DEC подобные по двум углам с пропорциональными сторонами BE и CE, а также AE и DE. Рассмотрим теперь треугольники AED и BEC, у которых сторона AE пропорциональна стороне DE, а сторона BE пропорциональна стороне CE, кроме того, равны углы  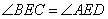 как вертикальные. Отсюда следует, что треугольники AED и BEC подобны по двум соответствующим пропорциональным сторонам и углу между ними. Так как у подобных треугольников соответствующие углы равны, то угол  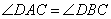. Утверждение доказано.

34.Задание 24. Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 8, BF = 15.

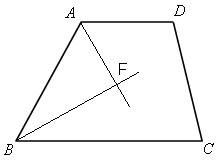
Решение.

Фигура ABCD – трапеция с основаниями AD и BC, то есть 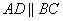 , и, следовательно,  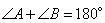. По условию задачи AF и BF – биссектрисы, значит,  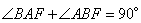. Так как сумма углов в треугольнике равна 180 градусов, то из треугольника ABF получаем угол

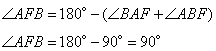
То есть треугольник ABF прямоугольный с гипотенузой AB. Найдем длину гипотенузы AB по теореме Пифагора:

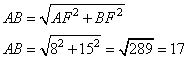
Ответ: 17.

35.Задание 25. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и ВС четырёхугольника пересекаются в точке К. Докажите, что треугольники KAB и KCD подобны.

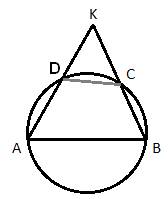
Решение.

Если вокруг четырехугольника можно описать окружность, то суммы его противоположных углов равны по 180 градусов, то есть 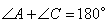 . Если положить угол  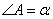, тогда угол  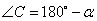, и, учитывая, что углы  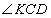 и 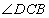  смежные, то угол

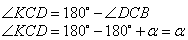
то есть он равен углу 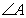 . Таким образом, треугольники KAB и KDC подобны по двум углам (угол K – общий). Утверждение доказано.

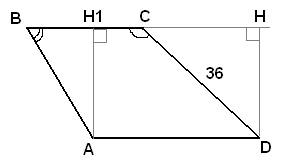
36.Задание 24. Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, a CD = 36.

Решение.

Проведем в трапеции две высоты 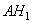  и DH (см. рисунок). Рассмотрим прямоугольный треугольник CHD с углом  . Следовательно, треугольник CHD также равнобедренный со сторонами CH=HD и основанием CD. Пусть сторона DH=x, соответственно, CH=x. Тогда по теореме Пифагора можно записать, что

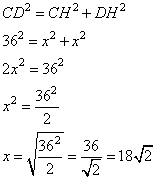
То есть 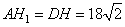 . Рассмотрим прямоугольный треугольник  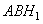, в котором известен один катет и угол  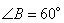. Так как синус угла B – это отношение противолежащего катета  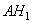 на гипотенузу AB, то можно записать

,

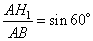откуда

.

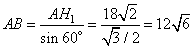Ответ: 12√6.

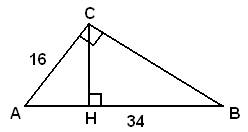
37.Задание 24. Катет и гипотенуза прямоугольного треугольника равны 16 и 34 соответственно. Найдите высоту, проведённую к гипотенузе.

Решение.

В соответствии со свойством о средних пропорциональных отрезках в прямоугольном треугольнике, катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. То есть в данном случае можно записать:

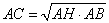
или в виде

,

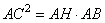откуда

.

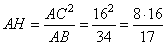Рассмотрим прямоугольный треугольник ACH, в котором известна гипотенуза AC и катет AH, следовательно, высоту CH можно найти по теореме Пифагора:

Ответ:  .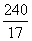

38.Задание 25. Биссектрисы углов B и C трапеции ABCD пересекаются в точке О, лежащей на стороне AD. Докажите, что точка О равноудалена от прямых АВ, ВС и CD.

Решение.

По условию задачи ABCD – трапеция с основаниями BC и AD и биссектрисами BO и CO, то есть углы 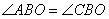  и  . И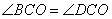з точки O проведем три перпендикуляра  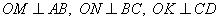 (по сути они будут являться расстояниями от точки O до прямых AB, BC и CD).

Теперь заметим, что треугольники BMO=BNO равны как прямоугольные по гипотенузе и острому углу: BO – общая гипотенуза; 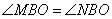 , так как BO – биссектриса. Из равенства треугольников следует, что OM=ON.

Аналогично для треугольников CNO=CKO, которые равны как прямоугольные по гипотенузе и острому углу: CO – общая гипотенуза; 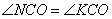 , так как CO – биссектриса. Следовательно, ON=OK.

Таким образом, имеем, что MO=NO=KO, а значит, точка O равноудалена от прямых AB, BC и CD. Положение доказано.

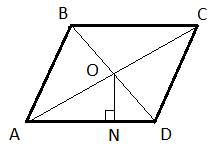
39.Задание 24. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 14, а одна из диагоналей ромба равна 56. Найдите углы ромба.

Решение.

Диагонали ромба являются биссектрисами его соответствующих углов, а точка пересечения O делит диагонали ромба пополам. Отсюда следует, что угол 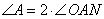 . Рассмотрим прямоугольный треугольник AON (прямоугольный, так как расстояние от точки O до AD – это перпендикуляр, опущенный из точки O). В этом треугольнике известен катет ON=14 и гипотенуза AO=AC:2=56:2=28. Тогда синус угла  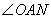 будет равен отношению противолежащего катета ON на гипотенузу AO:

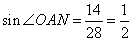
и угол

.

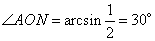Имеем, что угол

.

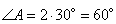Так как противоположные углы в ромбе равны, то 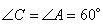 . Сумма односторонних углов в ромбе равна 180 градусов, то есть  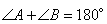 и

,

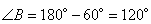соответственно,

.

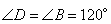Ответ: 60, 60, 120, 120.

40.Задание 25. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Докажите, что площади треугольников АОВ и COD равны.

Решение.

Запишем площадь треугольника ABO в виде:

,

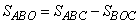где 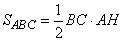  - площадь треугольника ABC;  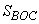 - площадь треугольника BOC. То есть площадь треугольника ABO можно представить как:

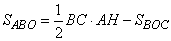.  (1)

Аналогично запишем площадь треугольника DCO, имеем:

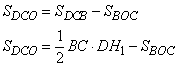
Так как 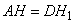 , то последнее выражение можно переписать в виде:

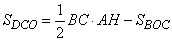.  (2)

Выражения (1) и (2) идентичны между собой и описывают площади треугольников ABO и DCO, то есть площади этих треугольников равны. Утверждение доказано.

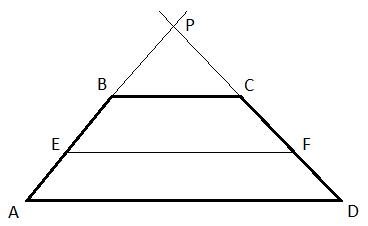
41.Задание 24. Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны АВ и CD в точках Е и F соответственно. Найдите длину отрезка EF, если AD = 48, ВС = 16, CF:DF = 5:3.

Решение.

Так как ABCD трапеция, то ее основания 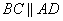 . По условию задачи прямая  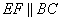 и 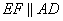 . Дополним построение, продолжим стороны AB  и CD так, чтобы они пересекались в точке P (см. рисунок). При этом треугольник PBC будет подобен треугольнику PAD по двум углам:  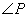 - общий, а углы  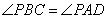 как соответственные при параллельных прямых BC, AD и секущей AP. Для подобных треугольников можно записать следующее соотношение:

.

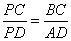Пусть PC=y, а коэффициент пропорциональности отрезков CF и DF равен x. Тогда CF=5x, DF=3x, CD=8x и соотношение сторон принимает вид:

,

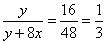откуда

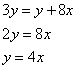
Теперь рассмотрим подобные треугольники PBC и PEF (также подобны по двум углам), из которых следует соотношение:

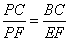
и после подстановки известных выражений, имеем:

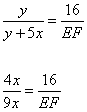
откуда

.

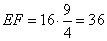Ответ: 36.

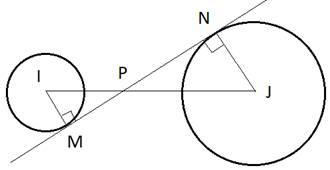
42.Задание 25. Окружности с центрами в точках I и J не имеют общих точек. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m:n. Докажите, что диаметры этих окружностей относятся как m:n.

Решение.

По условию задачи прямые IP:JP=m:n, а MN – касательная к окружностям в точках M и N, следовательно, 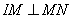  и 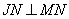 . Рассмотрим два прямоугольных треугольника IPM и JPN, которые подобны по двум углам: один угол у них прямой, а два других  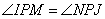 как вертикальные углы. Для подобных треугольников можно записать соотношение:

,

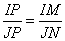но по условию 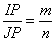 , следовательно,

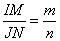
или, что эквивалентно, в виде

,

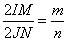где 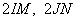  - диаметры соответствующих окружностей. Утверждение доказано.

43.Задание 24. Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 24, BF = 18.

Решение.

У трапеции ABCD основания 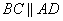 , следовательно, углы  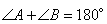 как внутренние односторонние при параллельных прямых. По условию задачи AF и BF – биссектрисы соответствующих углов, тогда сумма углов

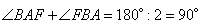
и, следовательно, угол 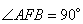  (так как сумма углов в треугольнике ABF равна 180 градусов). Таким образом, имеем прямоугольный треугольник AFB с гипотенузой AB, которую вычислим по теореме Пифагора:

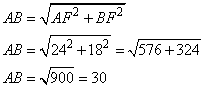
Ответ: 30.

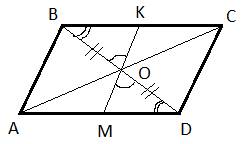
44.Задание 25. Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны ВС и AD в точках К и М соответственно. Докажите, что BK = DM.

Решение.

Точка пересечения O диагоналей AC и BD параллелограмма ABCD делит эти диагонали пополам, то есть BO=OD. Кроме того, углы 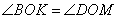  как вертикальные, а углы  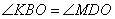 как накрест лежащие при параллельных прямых  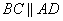 и секущей BD. Таким образом, треугольники BOK и DOM равны по стороне и двум с прилежащим к ней углам. Следовательно, и соответствующие стороны эти треугольников равны, то есть BK=DM. Утверждение доказано.

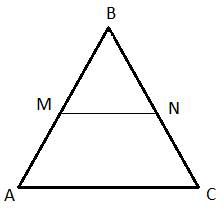
45.Задание 24. Прямая, параллельная стороне АС треугольника ABC, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 15, АС = 25, NC = 22.

Решение.

По условию задачи в треугольнике ABC прямая 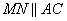 , следовательно, треугольники MBN и ABC подобны по двум углам: угол  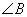 - общий, а углы  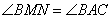 как соответственные при параллельных прямых MN, AC и секущей AB. Из подобия треугольников следует:

.

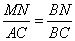Из рисунка видно, что 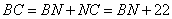 , подставляем числовые значения в отношение, имеем:

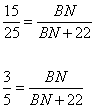
откуда

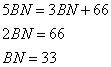
Ответ: 33.

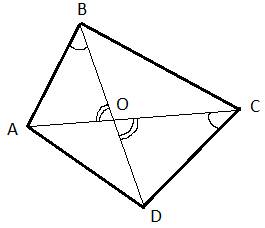
46.Задание 25. В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.

Решение.

Треугольники AOB и DOC подобны по двум углам: 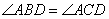  по условию задачи, а углы  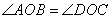 - как вертикальные. Из подобия треугольников можно записать следующее отношение:

.

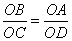Теперь рассмотрим треугольники BOC и AOD, которые также подобны по двум пропорциональным сторонам (полученное ранее отношение сторон) и углам 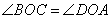  (равны как вертикальные углы), заключенным между этими сторонами. Как известно, в подобных треугольниках соответствующие углы равны, то есть  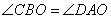, а значит и  . Утверждение доказано.

9