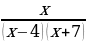Алгебра (7) Дата : 11.11.2024
Урок № 27
Тема урока : Переменные. Допустимые значения переменных
Образовательная цель: систематизировать и обобщить знания по теме «Буквенные выражения»; расширить представления учащихся о дробях числовых и алгебраических; закрепить разбором навыки решения примеров на нахождение допустимых значений переменных
Развивающая цель: развить познавательный интерес учащихся, наблюдательность, логику, память, внимание.
Воспитательная цель: точность аккуратность математической записи.
Тип урока. Урок формирования умений и навыков
Метод. Словесный, беседа, рассказ
Литература / основная/
Ход урока
-
Организационный момент
*проверка посещаемости;
*проверка готовности к уроку;
Проверка д/з выборочно.
2. Актуализация опорных базовых знаний на преобразование буквенных выражений:
1) Выполнить преобразование: 1,2b  (-3)
(-3)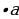 =
=
2) Выполнить преобразование: 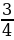
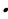 (4a -12) =
(4a -12) =
3) Выполнить преобразование: 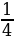
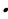 (b -16d) =
(b -16d) =
4) Что значит привести число к стандартному виду?
3.Мотивация учебной деятельности . Сообщение темы, цели , задачи урока. Вспоминаем дроби.
1) Дроби бывают числовые и алгебраические. Числовые –когда числитель и знаменатель дроби числа.
2) Алгебраические , когда числитель и знаменатель дроби многочлены.
Примеры алгебраических дробей:
а) 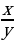 , читается - « x поделённое на y » или « икс игриковых » или
, читается - « x поделённое на y » или « икс игриковых » или
« x на y». x
б) 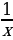 , читается - « одна иксовая » или « единица на икс » ;
, читается - « одна иксовая » или « единица на икс » ;
в) 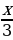 , читается - «одна третья икс» или « икс третьих» :
, читается - «одна третья икс» или « икс третьих» :
г) 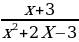 - алгебраическая дробь, числитель и знаменатель записан в виде многочленов.
- алгебраическая дробь, числитель и знаменатель записан в виде многочленов.
д) 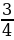 , это тоже алгебраическая дробь, только здесь многочлены вырожденные.
, это тоже алгебраическая дробь, только здесь многочлены вырожденные.
-
Формирование знаний умений навыков. Если дробь алгебраическая, мы делим, возникают ограничения –знаменатель не может быть равен нулю.
Те значения переменной (переменных) при которых знаменатель не равен нулю т.е. дробь «существует или имеет смысл» называют допустимые значения. При допустимых значениях дробь существует или имеет смысл.
Найти все значения переменной при которой дробь существует или дробь имеет смысл. Что имеют в виду – знаменатель не равен нулю ( 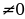 ).
).
Пример 1. Найти допустимые значения переменной
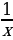 , при x
, при x 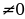 ;
;
Пример 2. Найти допустимые значения переменной
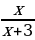 , при x+3
, при x+3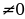 , x
, x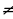 - 3
- 3
Пример 3. Найти допустимые значения переменной
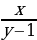 ; икс может быть любой, y - 1
; икс может быть любой, y - 1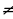 0 y
0 y 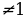 /
/
Пример 4. Найти допустимые значения переменной
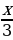 , любое число
, любое число
Пример 5.
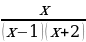 , допустимые значения знаменатель не должен быть равен нулю, в знаменателе произведение двух скобок. Каждая из них выступает как множитель. Рассмотрим случай когда два сомножителя равны нулю. Два сомножителя равны нулю когда каждый из них может быть равен нулю и первый,и второй. Применим эти знания на наших допустимых значениях.
, допустимые значения знаменатель не должен быть равен нулю, в знаменателе произведение двух скобок. Каждая из них выступает как множитель. Рассмотрим случай когда два сомножителя равны нулю. Два сомножителя равны нулю когда каждый из них может быть равен нулю и первый,и второй. Применим эти знания на наших допустимых значениях.
Имеем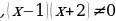 . Значит
. Значит 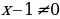
и 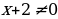 . Значит : x
. Значит : x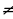 1, x
1, x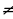 - 2.
- 2.
Пример 6.
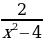 , Надо понять, когда
, Надо понять, когда 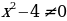 .
.
Здесь спряталась формула разности квадратов 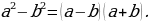 В нашем случае
В нашем случае 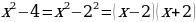 в знаменателе при разложении образуются два сомножителя
в знаменателе при разложении образуются два сомножителя 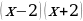 . Допустимые значения x
. Допустимые значения x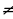 2, x
2, x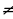 - 2.
- 2.
Пример 7. Найти допустимые значения переменной
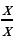 Случай не стандартный
Случай не стандартный 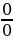 ; на ноль делить нельзя и ноль на ноль математическая неопределённость . Решение одно . Все допустимые значения , но только не нуль. при x
; на ноль делить нельзя и ноль на ноль математическая неопределённость . Решение одно . Все допустимые значения , но только не нуль. при x 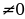 ;
;
Пример 8. Найдите допустимые значения переменной:
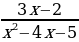
Рассмотрим знаменатель
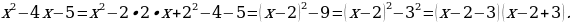
Наша дробь будет существовать при условии если? :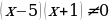
Значит : x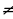 5, x
5, x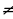 - 1.
- 1.
6.Подведение итогов урока. Анализ работы в классе. Оценивание.
7. Домашнее задание: Найти допустимые значения переменной: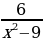 ,
, 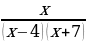







 (-3)
(-3)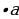 =
=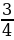
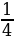
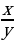 , читается - « x поделённое на y » или « икс игриковых » или
, читается - « x поделённое на y » или « икс игриковых » или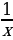 , читается - « одна иксовая » или « единица на икс » ;
, читается - « одна иксовая » или « единица на икс » ;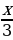 , читается - «одна третья икс» или « икс третьих» :
, читается - «одна третья икс» или « икс третьих» :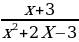 - алгебраическая дробь, числитель и знаменатель записан в виде многочленов.
- алгебраическая дробь, числитель и знаменатель записан в виде многочленов.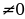 ).
).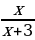 , при x+3
, при x+3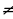 - 3
- 3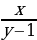 ; икс может быть любой, y - 1
; икс может быть любой, y - 1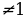 /
/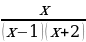 , допустимые значения знаменатель не должен быть равен нулю, в знаменателе произведение двух скобок. Каждая из них выступает как множитель. Рассмотрим случай когда два сомножителя равны нулю. Два сомножителя равны нулю когда каждый из них может быть равен нулю и первый,и второй. Применим эти знания на наших допустимых значениях.
, допустимые значения знаменатель не должен быть равен нулю, в знаменателе произведение двух скобок. Каждая из них выступает как множитель. Рассмотрим случай когда два сомножителя равны нулю. Два сомножителя равны нулю когда каждый из них может быть равен нулю и первый,и второй. Применим эти знания на наших допустимых значениях.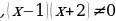 . Значит
. Значит 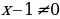
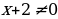 . Значит : x
. Значит : x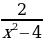 , Надо понять, когда
, Надо понять, когда 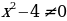 .
. 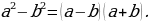 В нашем случае
В нашем случае 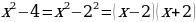 в знаменателе при разложении образуются два сомножителя
в знаменателе при разложении образуются два сомножителя 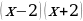 . Допустимые значения x
. Допустимые значения x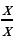 Случай не стандартный
Случай не стандартный 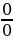 ; на ноль делить нельзя и ноль на ноль математическая неопределённость . Решение одно . Все допустимые значения , но только не нуль. при x
; на ноль делить нельзя и ноль на ноль математическая неопределённость . Решение одно . Все допустимые значения , но только не нуль. при x 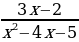
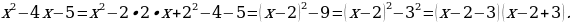
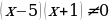
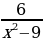 ,
,