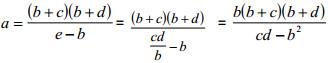Материалы для подготовки к муниципальному этапу олимпиады по математике
№1
33 богатыря выходят в дозор 33 дня. В первый день должен выйти один богатырь, во второй – два, в третий – три, и так далее, в последний день – все богатыри. Сможет ли дядька Черномор организовать дозоры так, чтобы все богатыри вышли в дозор одинаковое количество раз?
Ответ: сможет.
Решение. Так как 1 + 2 + … + 33 = 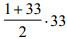 = 17×33, то каждый богатырь должен выйти в дозор 17 раз. Пусть, например, Черномор пронумерует богатырей и в первые 16 дней богатыри выходят в дозор в соответствии со своими номерами: в первый день –богатырь с номером один, во второй – с номерами 1 и 2, и так далее, в шестнадцатый день –богатыри с номерами от 1 до 16. В следующие 16 дней порядок выхода такой: в семнадцатый день – богатыри с номерами от 17 до 33, в восемнадцатый – с номерами от 16 до 33, и так далее, в тридцать второй день : богатыри с номерами от 2 до 33. Таким образом, за эти дни каждый богатырь побывает в дозоре 16 раз, а в последний день выйдут все.
= 17×33, то каждый богатырь должен выйти в дозор 17 раз. Пусть, например, Черномор пронумерует богатырей и в первые 16 дней богатыри выходят в дозор в соответствии со своими номерами: в первый день –богатырь с номером один, во второй – с номерами 1 и 2, и так далее, в шестнадцатый день –богатыри с номерами от 1 до 16. В следующие 16 дней порядок выхода такой: в семнадцатый день – богатыри с номерами от 17 до 33, в восемнадцатый – с номерами от 16 до 33, и так далее, в тридцать второй день : богатыри с номерами от 2 до 33. Таким образом, за эти дни каждый богатырь побывает в дозоре 16 раз, а в последний день выйдут все.
Это решение можно изложить в общем виде, например, так. Например, пусть в k-ый день, где 1 ≤ k ≤ 16, выходят богатыри с номерами от 1 до k, а все богатыри, которые не вышли в в k-ый день, выходят в день, имеющий номер 33 – k. Тогда за каждую пару дней вида (k; 33 – k) в дозоре побывают все богатыри, и каждый выйдет 16 раз – по количеству таких пар. После этого они все вместе выйдут в последний день.
Критерии проверки
“+” Приведено полное обоснованное решение
“±” Приведен верный алгоритм, но рассуждения не полны или содержат неточности
“–” Приведен только ответ
“–” Приведено неверное решение или оно отсутствует
№ 2
Содержание ↑
Существуют ли такие попарно различные числа a, b и c, что число a является корнем квадратного трехчлена x2 – 2bx + c2, число b является корнем квадратного трехчлена x2 – 2cx + a2, а число c является корнем квадратного трехчлена x2 – 2ax + b2?
Ответ: не существуют.
Решение. Предположим, что такие числа нашлись. Тогда выполняются равенства: a2 – 2ba + c2 = 0, b2 – 2cb + a2 = 0 и с2 – 2aс + b2 = 0. Сложим эти равенства. Перегруппировав и выделив полные квадраты, получим: (a – b)2 + (b – c)2 + (c – a)2 = 0. Это возможно только в случае, когда a =b = c, что противоречит условию.
Критерии проверки
“+” Приведено полное обоснованное решение
“±”Приведено верное в целом решение, содержащее незначительные пробелы или неточности
“-/+” Присутствует только верная идея сложения равенств, не доведенная до конца
“–” Приведен только ответ
“–” Приведено неверное решение или оно отсутствует
Задание 3
Содержание ↑
Две окружности пересекаются в точках А и В. Оказалось, что радиусы ОА и ОВ первой окружности являются касательными ко второй окружности. Через точку А проведена прямая, которая вторично пересекает окружности в точках М и N. Докажите, что MB⊥NB.
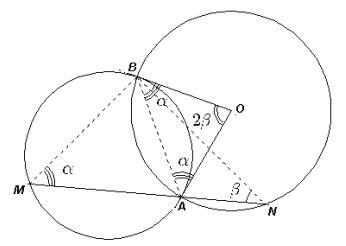
Рисунок 10.3.a
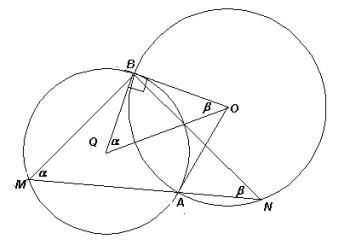
Рисунок 10.3.б
Решение. Пусть ∠BMN = ∝, ∠BNM = β (см. рис. 10.3 а, б).
Первый способ. См. рис. 10.3а. Заметим, что ∠ОАВ = ∠ОВА = a (по теореме об угле между касательной и хордой), ∠АОВ = 2β (центральный угол). Из треугольника АОВ: 2∝ + 2β = 180°, значит ∝ + β = 90°. Следовательно, ∠MBN = 90°, что и требовалось.
Второй способ. См. рис. 10.3б. Пусть Q – центр второй окружности, тогда ∠ОQВ = 1/2 ∠АQB = ∝, ∠QOВ =1/2 ∠АOB = β. Следовательно, треугольники QBO и MBN подобны. Но ∠QBO = 90° (перпендикулярность касательной и радиуса), значит, ∠MBN = 90°, что и требовалось.
Существуют и другие способы рассуждений, например, можно использовать, что четырехугольник OAQB – вписанный (см. рис. 10.3б).
Критерии проверки
“+” Приведено полное обоснованное решение
“±” Приведено верное в целом решение, содержащее незначительные пробелы или неточности
“–” Приведено неверное решение или оно отсутствует
Задание 4
Содержание ↑
Выписаны все делители некоторого натурального числа, кроме единицы и его самого. Какие-то два числа из этого списка отличаются в шесть раз. А во сколько раз отличаются два самых больших числа из этого списка?
Ответ: в полтора раза.
Решение. Пусть среди делителей числа N есть числа а и 6а, тогда N делится на 6а.
Следовательно N делится на 2 и на 3, то есть 2 и 3 – два наименьших числа в списке. Тогда два наибольших числа в списке – это N/3 и N/2. Их отношение: N/2 : N/3 = 3/2.
Критерии проверки
“+” Приведено полное обоснованное решение
“±” Приведено верное в целом решение, содержащее незначительные пробелы или неточности
“-/+” Верный ответ получен, исходя из того, что 2 и 3 – наименьшие числа в списке делителей, ноих присутствие в этом списке не доказано
“-/+” Верный ответ получен, исходя из рассмотрения конкретных примеров
“–” Приведен только ответ
“–” Приведено неверное решение или оно отсутствует
Задание 5
Содержание ↑
На сторонах АВ и ВС треугольника АВС отмечены точки X и Y соответственно. Отрезки CX и AY пересекаются в точке T. Докажите, что площадь треугольника XBY больше площади треугольника XTY.
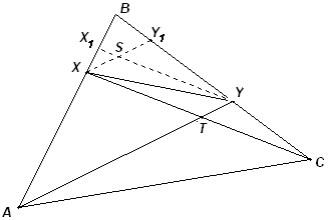
Рисунок 10.5.a
Решение. Первый способ. Отметим на отрезке BX точку X1 так, что YX1 || CX (см. рис. 10.5а). Аналогично, на отрезке BY выберем точку Y1 так, что XY1 || AY. Пусть отрезки YX1 и XY1 пересекаются в точке S. Тогда XSYT – параллелограмм, поэтому равны треугольники XSY и YTX, следовательно, равны и их площади. Но площадь треугольника XBY больше площади треугольника XSY, значит, SXBY SXTY.
Отметив указанным образом точку X1, можно рассуждать иначе: из подобия треугольников XAT и X1AY следует, что YX1 TX. Тогда SXTY XYX1 XBY.
Задача допускает также многочисленные вычислительные решения. Приведём одно из них.
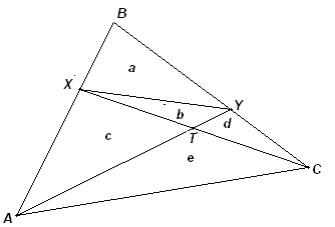
Рисунок 10.5.б
Второй способ. Обозначим площади треугольников буквами a, b, c, d, e так, как показано на рис. 10.5б.
Так как площади треугольников с общей высотой относятся как их основания, то b/d = XT/TC = c/e. Тогда e = cd/b . Аналогично,
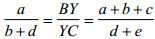
Отсюда a(d + e) = (a + b + c)(b + d).
Выразим а из этого равенства, учитывая найденное выражение для e:
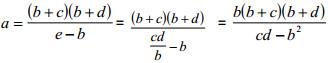
Тогда требуемое неравенство a b следует из того, что
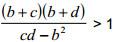
Последнее неравенство выполняется, так как числитель дроби больше cd, а знаменатель меньше, чем cd.
Критерии проверки
“+” Приведено полное обоснованное решение
“±” Приведено верное в целом решение, содержащее незначительные пробелы или неточности
“–” Приведено неверное решение или оно отсутствует
Задание 6
Содержание ↑
Есть две коробки, в одной 2017 конфет, а в другой 2018. Играют двое, ходят по очереди. За один ход каждый может съесть любое количество конфет, отличное от нуля, из любой коробки.
Правила игры не допускают, чтобы после какого-то хода число конфет в одной из коробок делилось на число конфет в другой. Проигрывает тот, кто не может сделать ход, не нарушив этого условия.
Кто сможет выиграть: начинающий игру или второй игрок, как бы ни играл его соперник?
Ответ: сможет выиграть первый.
Решение. Для того, чтобы выиграть, первый игрок после каждого своего хода должен создавать ситуацию, когда в одной из коробок 2n конфет, а в другой 2n + 1 (n – натуральное число).
В такой ситуации он заведомо не проигрывает.
Сначала он съедает две конфеты из второй коробки и получает нужную ситуацию. В дальнейшем, в ответ на любой ход второго игрока первый будет восстанавливать такое распределение конфет. Покажем, что он сможет это делать. Возможны 4 случая.
Второй ест четное количество конфет из той коробки, где их 2n. Тогда в ней останется 2m конфет (m 0, иначе второй проиграл). В ответ первый съедает из другой коробки такое же количество конфет, и в ней остается 2m + 1.
Второй ест нечетное количество конфет из той коробки, где их 2n. Тогда в ней останется 2m + 1 конфет (m 0, иначе второй проиграл). В ответ первый съедает из другой коробки на две конфеты больше и в ней остается 2m.
Второй ест нечетное количество конфет из той коробки, где их 2n + 1. Тогда в ней останется 2m конфет, где 0 m n (иначе второй проиграл). В ответ первый съедает из другой коробки на две конфеты меньше и в ней остается 2m + 1.
Второй ест четное количество конфет из той коробки, где их 2n + 1. Тогда в ней останется 2m + 1 конфет (m 0, иначе второй проиграл). В ответ первый съедает из другой коробки такое же количество конфет, и в ней остается 2m.
Действуя таким образом, первый (если второй до этого ни разу не ошибётся) сведет игру к тому, что в одной коробке останется две конфеты, а в другой три, и после этого второй проигрывает, какой бы ход он ни сделал.
Критерии проверки
“+” Приведено полное обоснованное решение
“±” Приведено верное в целом решение, содержащее незначительные пробелы или неточности
“-/+” Приведена верная стратегия, но она не обоснована
“–” Приведен только ответ или ответ, полученный рассмотрением конкретных примеров
“–” Приведено неверное решение или оно отсутствует