Ф.И._______________________________ вариант1
Решение.
Треугольник BOD — прямоугольный, таким образом,  Углы ABD и ACD опираются на одну дугу, следовательно, эти углы равны. Таким образом,
Углы ABD и ACD опираются на одну дугу, следовательно, эти углы равны. Таким образом, 
Ответ: 65.
Ответ: 65
311523
65
1. 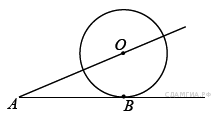
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 20 см, AO = 29 см.
Ответ________________
Решение.
Проведем OB — радиус окружности с центром O. Так как OB — радиус , проведенный в точку касания, то 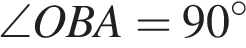 , таким образом треугольник AOB прямоугольный.
, таким образом треугольник AOB прямоугольный.
По теореме Пифагора: 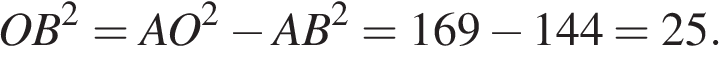 Таким образом,
Таким образом, 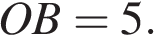
Ответ: 5.
Ответ: 5
311681
5
2.
Решение.
Проверим каждое из утверждений.
1) «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой» — верно, это аксиома планиметрии.
2) «Треугольник со сторонами 1, 2, 4 существует» — неверно: для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.
3) «Если в ромбе хотя бы 2 угла равны 90°, то такой ромб — квадрат» — верно, в этом случае противоположный угол тоже будет равен 90°, а значит и два других (равных) угла будут равны по 90°.
4) «Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.» — неверно, центр описанной вокруг прямоугольного треугольника окружности, лежит на его стороне.
Ответ: 1; 3.
Ответ: 1; 3
311684
1; 3
Решение.
Угол AOB смежный с углом AOD, таким образом,  Центральный угол AOB и вписанный угол ACB опираются на одну дугу. Таким образом,
Центральный угол AOB и вписанный угол ACB опираются на одну дугу. Таким образом, 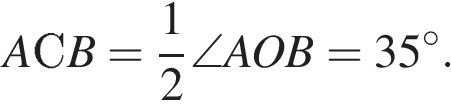
Ответ: 35
311517
35
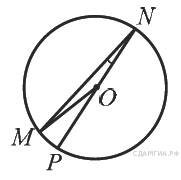 Найдите градусную меру
Найдите градусную меру 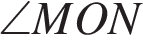 , если известно, NP — диаметр, а градусная мера
, если известно, NP — диаметр, а градусная мера 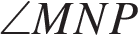 равна 22°.
равна 22°.
Ответ________________
4. 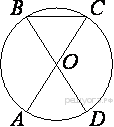 AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.
Ответ_________________________
5.. 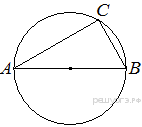 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.
Ответ________________
Ф.И._________________________________ Вариант2
Решение.
Треугольник BOD — прямоугольный, таким образом,  Углы ABD и ACD опираются на одну дугу, следовательно, эти углы равны. Таким образом,
Углы ABD и ACD опираются на одну дугу, следовательно, эти углы равны. Таким образом, 
Ответ: 65.
Ответ: 65
311523
65
1.  К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
Ответ________________
Решение.
Проведем OB — радиус окружности с центром O. Так как OB — радиус , проведенный в точку касания, то 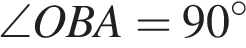 , таким образом треугольник AOB прямоугольный.
, таким образом треугольник AOB прямоугольный.
По теореме Пифагора: 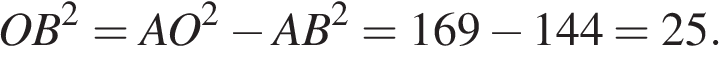 Таким образом,
Таким образом, 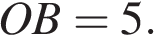
Ответ: 5.
Ответ: 5
311681
5
2.
Решение.
Проверим каждое из утверждений.
1) «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой» — верно, это аксиома планиметрии.
2) «Треугольник со сторонами 1, 2, 4 существует» — неверно: для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.
3) «Если в ромбе хотя бы 2 угла равны 90°, то такой ромб — квадрат» — верно, в этом случае противоположный угол тоже будет равен 90°, а значит и два других (равных) угла будут равны по 90°.
4) «Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.» — неверно, центр описанной вокруг прямоугольного треугольника окружности, лежит на его стороне.
Ответ: 1; 3.
Ответ: 1; 3
311684
1; 3
Решение.
Угол AOB смежный с углом AOD, таким образом,  Центральный угол AOB и вписанный угол ACB опираются на одну дугу. Таким образом,
Центральный угол AOB и вписанный угол ACB опираются на одну дугу. Таким образом, 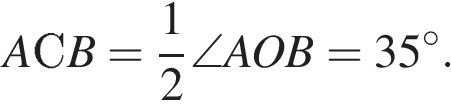
Ответ: 35
311517
35
 Найдите градусную меру
Найдите градусную меру 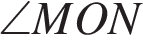 , если известно, NP — диаметр, а градусная мера
, если известно, NP — диаметр, а градусная мера 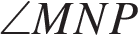 равна 18°.
равна 18°.
Ответ________________
3.Точки 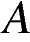 и
и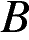 делят окружность на две дуги, длины
делят окружность на две дуги, длины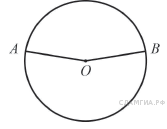 которых относятся как 14:10. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.Ответ________________
которых относятся как 14:10. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.Ответ________________
4.  AC и BD — диаметры окружности с центром O. Угол ACB равен 82°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD — диаметры окружности с центром O. Угол ACB равен 82°. Найдите угол AOD. Ответ дайте в градусах.
Ответ_________________________
5..  Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 36°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 36°. Ответ дайте в градусах.
Ответ________________
Ф.И.____________________________ Решение.
Треугольник MON — равнобедренный. Тогда  .
.
Ответ: 144.
Ответ: 144
311319
144
Решение.
Угол ABC — вписанный и опирается на диаметр AC. Таки образом, 
Ответ: 90.
Ответ: 90
311507
90
Решение.
Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания с касательной, следствием чего является перпендикулярность OB и AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB: по теореме Пифагора катет равен 5.
Ответ: 5.
Ответ: 5
38
5
Решение.
Рассмотрим треугольник AOB: он равнобедренный, т. к. состоит из двух отрезков, равных радиусу.
Углы при основании равнобедренного треугольника равны. Обозначим угол AOB буквой 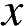 , тогда
, тогда 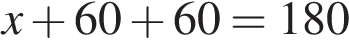 , где
, где 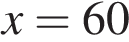 . Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.
. Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.
Ответ: 6.
Ответ: 6
90
6
Решение.
Так как OA и OB- радиусы, то треугольник AOB — равнобедренный. Однако, в равнобедренном треугольнике 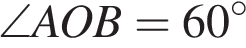 , тогда треугольник является правильным. Таким образом, хорда
, тогда треугольник является правильным. Таким образом, хорда 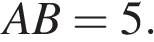
Ответ: 5.
Ответ: 5
311487
5
Вариант 3
1. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 15 см, AO = 17 см.
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 15 см, AO = 17 см.
Ответ________________
Решение.
Рассмотрим треугольники COD и AOB: они равны по двум сторонам и углу между ними. Мало того, треугольники равнобедренные; значит, можно сделать вывод, что угол OAB и OCD равны.
Ответ: 70.
Ответ: 70
116
70
Решение.
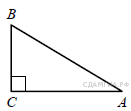
Тангенс угла равен отношению противолежащего углу катета к прилежащему:
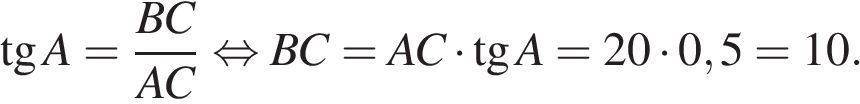
Ответ: 10.
Ответ: 10
311760
10
Решение.
Рассмотрим треугольник AOB: он равнобедренный, т. к. состоит из двух отрезков, равных радиусу. Углы при основании равнобедренного треугольника равны. Обозначим угол BAO буквой 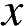 , тогда
, тогда  , где
, где 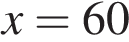 . Треугольник, у которого все углы равны, — равносторонний треугольник; значит, AB = 5.
. Треугольник, у которого все углы равны, — равносторонний треугольник; значит, AB = 5.
Ответ: 5.
Ответ: 5
64
5
2. Точки
Точки 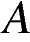 и
и 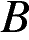 делят окружность на две дуги, длины которых относятся как 7:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.Ответ________________
делят окружность на две дуги, длины которых относятся как 7:11. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.Ответ________________
Решение.
Дуги окружности относятся как 9:11, что в сумме дает 20 частей.
Длина меньшей дуги составляет  от всей окружности. Имеем:
от всей окружности. Имеем:
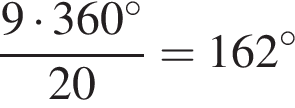
.
Так как угол AOB — центральный, то он равен той дуге на которую он опирается. Таким образом,  .
.
Ответ: 162.
Ответ: 162
311483
162
3.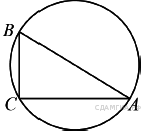
В треугольнике ABC угол C равен 90°, AC = 30 ,BC = 40.Найдите радиус окружности, описанной около этого треугольника.
Ответ________________
4.  AC и BD — диаметры окружности с центром O. Угол ACB равен 86°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD — диаметры окружности с центром O. Угол ACB равен 86°. Найдите угол AOD. Ответ дайте в градусах.
Ответ_________________________
5..  Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 42°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 42°. Ответ дайте в градусах.
Ответ________________
Ф.И._________________________________ Вариант № 4
Решение.
Построим OA и OC радиусы. Найдем центральный угол AOC:
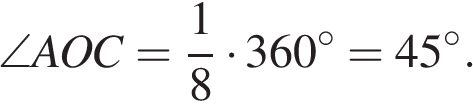
Угол ABC — вписанный и опирается на ту же дугу. Таким образом,
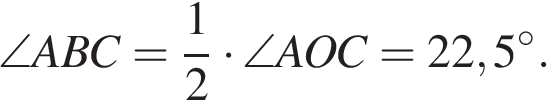
Ответ: 22,5.
Ответ: 22,5
311503
22,5
1. 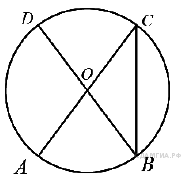 В окружности с центром
В окружности с центром 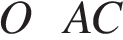 и
и 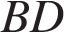 — диаметры. Угол
— диаметры. Угол  равен 26°. Найдите угол
равен 26°. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.
Ответ________________
Решение.
Так как 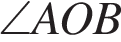 является центральным, а
является центральным, а 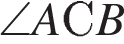 — вписанным и они опираются на одну дугу, то по свойству вписанного угла
— вписанным и они опираются на одну дугу, то по свойству вписанного угла 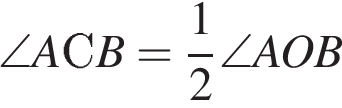 . Таким образом,
. Таким образом, 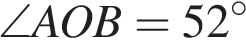 . Найдем
. Найдем 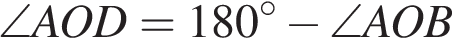 , так как BD — диаметр. Таким образом
, так как BD — диаметр. Таким образом  .
.
Ответ: 128.
Ответ: 128
311398
128
Решение.
Найдем отрезок DO: 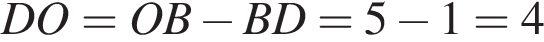 . Так как OB перпендикулярен AC, то треугольник AOD — прямоугольный. По теореме Пифагора имеем:
. Так как OB перпендикулярен AC, то треугольник AOD — прямоугольный. По теореме Пифагора имеем:  . Треугольник AOC — равнобедренный так как AO = OC = r, тогда AD = DC. Таким образом,
. Треугольник AOC — равнобедренный так как AO = OC = r, тогда AD = DC. Таким образом, 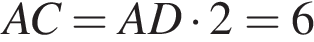 .
.
Ответ: 6.
Ответ: 6
311410
6
2. 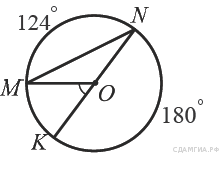 Найдите
Найдите 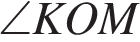 , если известно, что градусная мера дуги
, если известно, что градусная мера дуги 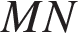 равна 124°, а градусная мера дуги
равна 124°, а градусная мера дуги 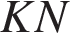 равна 180°.
равна 180°.
Ответ________________
3. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 24 см, AO = 26 см.Ответ________________
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 24 см, AO = 26 см.Ответ________________
3. Точки 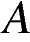 и
и 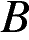 делят окружность на две дуги, длины которых относятся как 4:5. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
делят окружность на две дуги, длины которых относятся как 4:5. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.

Ответ________________
4.  AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.
Ответ_________________________
5..  Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.
Ответ________________
Ф.И._________________________________Вариант5
Решение.
Треугольник BOD — прямоугольный, таким образом,  Углы ABD и ACD опираются на одну дугу, следовательно, эти углы равны. Таким образом,
Углы ABD и ACD опираются на одну дугу, следовательно, эти углы равны. Таким образом, 
Ответ: 65.
Ответ: 65
311523
65
1.. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
Ответ________________
Решение.
Проведем OB — радиус окружности с центром O. Так как OB — радиус , проведенный в точку касания, то 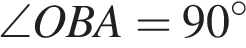 , таким образом треугольник AOB прямоугольный.
, таким образом треугольник AOB прямоугольный.
По теореме Пифагора: 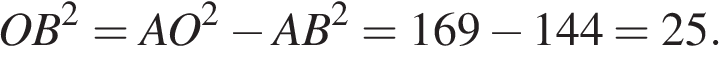 Таким образом,
Таким образом, 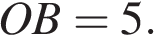
Ответ: 5.
Ответ: 5
311681
5
2.
Решение.
Проверим каждое из утверждений.
1) «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой» — верно, это аксиома планиметрии.
2) «Треугольник со сторонами 1, 2, 4 существует» — неверно: для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.
3) «Если в ромбе хотя бы 2 угла равны 90°, то такой ромб — квадрат» — верно, в этом случае противоположный угол тоже будет равен 90°, а значит и два других (равных) угла будут равны по 90°.
4) «Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.» — неверно, центр описанной вокруг прямоугольного треугольника окружности, лежит на его стороне.
Ответ: 1; 3.
Ответ: 1; 3
311684
1; 3
Решение.
Угол AOB смежный с углом AOD, таким образом,  Центральный угол AOB и вписанный угол ACB опираются на одну дугу. Таким образом,
Центральный угол AOB и вписанный угол ACB опираются на одну дугу. Таким образом, 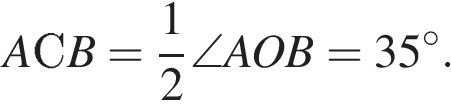
Ответ: 35
311517
35
 Найдите градусную меру
Найдите градусную меру 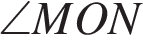 , если известно, NP — диаметр, а градусная мера
, если известно, NP — диаметр, а градусная мера 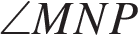 равна 18°.
равна 18°.
Ответ________________
Решение.
Треугольник MON — равнобедренный. Тогда  .
.
Ответ: 144.
Ответ: 144
311319
144
Решение.
Угол ABC — вписанный и опирается на диаметр AC. Таки образом, 
Ответ: 90.
Ответ: 90
311507
90
Решение.
Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания с касательной, следствием чего является перпендикулярность OB и AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB: по теореме Пифагора катет равен 5.
Ответ: 5.
Ответ: 5
38
5
Решение.
Рассмотрим треугольник AOB: он равнобедренный, т. к. состоит из двух отрезков, равных радиусу.
Углы при основании равнобедренного треугольника равны. Обозначим угол AOB буквой 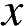 , тогда
, тогда 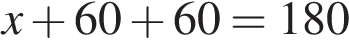 , где
, где 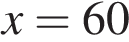 . Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.
. Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.
Ответ: 6.
Ответ: 6
90
6
Решение.
Так как OA и OB- радиусы, то треугольник AOB — равнобедренный. Однако, в равнобедренном треугольнике 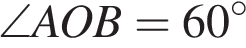 , тогда треугольник является правильным. Таким образом, хорда
, тогда треугольник является правильным. Таким образом, хорда 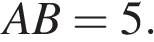
Ответ: 5.
Ответ: 5
311487
5
3. 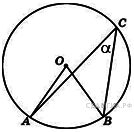 Найдите величину (в градусах) вписанного угла
Найдите величину (в градусах) вписанного угла  , опирающегося на хорду
, опирающегося на хорду 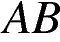 , равную радиусу окружности. Ответ________________
, равную радиусу окружности. Ответ________________
4.  AC и BD — диаметры окружности с центром O. Угол ACB равен 82°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD — диаметры окружности с центром O. Угол ACB равен 82°. Найдите угол AOD. Ответ дайте в градусах.
Ответ_________________________
5..  Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 28°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 28°. Ответ дайте в градусах.
Ответ________________
Ф.И._________________________________Вариант6
Решение.
Треугольник BOD — прямоугольный, таким образом,  Углы ABD и ACD опираются на одну дугу, следовательно, эти углы равны. Таким образом,
Углы ABD и ACD опираются на одну дугу, следовательно, эти углы равны. Таким образом, 
Ответ: 65.
Ответ: 65
311523
65
1. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 6 см, AO = 10 см.

Ответ________________
Решение.
Проведем OB — радиус окружности с центром O. Так как OB — радиус , проведенный в точку касания, то 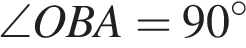 , таким образом треугольник AOB прямоугольный.
, таким образом треугольник AOB прямоугольный.
По теореме Пифагора: 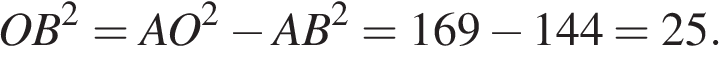 Таким образом,
Таким образом, 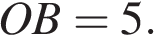
Ответ: 5.
Ответ: 5
311681
5
2. Решение.
Проверим каждое из утверждений.
1) «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой» — верно, это аксиома планиметрии.
2) «Треугольник со сторонами 1, 2, 4 существует» — неверно: для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.
3) «Если в ромбе хотя бы 2 угла равны 90°, то такой ромб — квадрат» — верно, в этом случае противоположный угол тоже будет равен 90°, а значит и два других (равных) угла будут равны по 90°.
4) «Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.» — неверно, центр описанной вокруг прямоугольного треугольника окружности, лежит на его стороне.
Ответ: 1; 3.
Ответ: 1; 3
311684
1; 3
Решение.
Угол AOB смежный с углом AOD, таким образом,  Центральный угол AOB и вписанный угол ACB опираются на одну дугу. Таким образом,
Центральный угол AOB и вписанный угол ACB опираются на одну дугу. Таким образом, 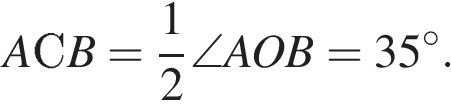
Ответ: 35
311517
35
Найдите градусную меру 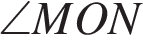 , если известно, NP — диаметр, а градусная мера
, если известно, NP — диаметр, а градусная мера 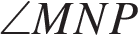 равна 21°.
равна 21°.

Ответ________________
3. Точки 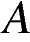 и
и 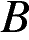 делят окружность на две дуги, длины которых относятся как 10:8. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.
делят окружность на две дуги, длины которых относятся как 10:8. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.

Ответ________________
4.  AC и BD — диаметры окружности с центром O. Угол ACB равен 59°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD — диаметры окружности с центром O. Угол ACB равен 59°. Найдите угол AOD. Ответ дайте в градусах.
Ответ_________________________
5..  Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 26°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 26°. Ответ дайте в градусах.
Ответ________________
Решение.
Треугольник MON — равнобедренный. Тогда  .
.
Ответ: 144.
Ответ: 144
311319
144
Решение.
Угол ABC — вписанный и опирается на диаметр AC. Таки образом, 
Ответ: 90.
Ответ: 90
311507
90
Решение.
Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания с касательной, следствием чего является перпендикулярность OB и AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB: по теореме Пифагора катет равен 5.
Ответ: 5.
Ответ: 5
38
5
Решение.
Рассмотрим треугольник AOB: он равнобедренный, т. к. состоит из двух отрезков, равных радиусу.
Углы при основании равнобедренного треугольника равны. Обозначим угол AOB буквой 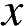 , тогда
, тогда 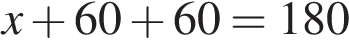 , где
, где 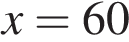 . Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.
. Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.
Ответ: 6.
Ответ: 6
90
6
Решение.
Так как OA и OB- радиусы, то треугольник AOB — равнобедренный. Однако, в равнобедренном треугольнике 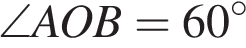 , тогда треугольник является правильным. Таким образом, хорда
, тогда треугольник является правильным. Таким образом, хорда 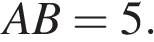
Ответ: 5.
Ответ: 5
311487
5
Решение.
Угол AOB является центральным углом, ACB — вписанным. Оба угла опираются на одну и ту же дугу, следовательно, угол AOB в два раза больше угла ACB.
Ответ: 24.
Ответ: 24
311956
24






 Найдите градусную меру
Найдите градусную меру  AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD — диаметры окружности с центром O. Угол ACB равен 79°. Найдите угол AOD. Ответ дайте в градусах. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах. которых относятся как 14:10. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.Ответ________________
которых относятся как 14:10. Найдите величину центрального угла, опирающегося на меньшую из дуг. Ответ дайте в градусах.Ответ________________

 В окружности с центром
В окружности с центром 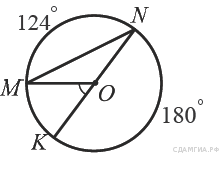 Найдите
Найдите  Найдите величину (в градусах) вписанного угла
Найдите величину (в градусах) вписанного угла 









