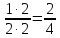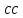| Организационный момент Цели: эмоциональная, психологическая и мотивационная подготовка учащихся к восприятию учебного материала | Приветствие детей (запись в тетрадях числа, «классная работа». Угадайте, какие слова надо вставить? Каждый может за версту Видеть дробную ЧЕРТУ Над чертой – ЧИСЛИТЕЛЬ, знайте, Под чертою – ЗНАМЕНАТЕЛЬ Дробь такую непременно Надо звать ОЫКНОВЕННОЙ Посмотрите, что за дробь – Дробь обыкновенная. Проведем сегодня с ней Действия мгновенные… | Записывают число, классная работа.
Вставляют слова, которые пропускает учитель. | Мотив Выделение проблемы | целеполагание | Формулировка проблемы Формулировка цели |
| Проверка домашнего задания. Цели: актуализировать те знания, которые необходимы для решения проблемы | Из каких частей состоит дробь? Что записывается под дробной чертой? Что показывает знаменатель? Что записывается над дробной чертой? Что он показывает? Как мы сравниваем дроби с одинаковым числителем?
Как мы сравниваем дроби с одинаковыми знаменателями? Сравните дроби:  ; ;  и и 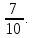 | Числитель и знаменатель Знаменатель На сколько частей разделили целое Числитель Сколько частей взяли Из двух дробей с одинаковыми числителями больше та дробь, числитель которой больше Из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше. Сравнивают дроби, объясняя какая больше. | Рефлексия Смысловое чтение | Самоконтроль Планируем исследование, формулируем адекватные методы и средства (понятия и правила)
| Аргументация Построение речевого высказывания, коллективная работа, построение понятия для собеседника (высказывание) |
| Наблюдение над фактами Цели: при помощи сравнения и сопоставления языковых фактов, выделить существенные признаки, понятия (или правила)
Обобщение структурных и систематических признаков понятия (правила) Цель: научить обобщать (делать вывод)
| На доске записаны обыкновенные дроби. Давайте их сравним.  и и 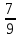
Сравним  и и 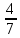
Сравним  и и 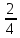 (создание проблемной ситуации) (создание проблемной ситуации)
Как вы думаете, чем мы сегодня будем заниматься?
Какая цель нашего урока?
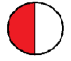
(Построение проекта выхода из затруднения) Давайте с вами разберем какая же дробь больше  или или 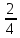 . . У Вас на листочках нарисован круг (раздаточный материал). Разделите круг на две доли. Заштрихуйте одну долю. (обращаю внимание на экран, где изображен круг, разделенный на две части, одна из которых закрашена)
Какой обыкновенной дроби соответствует закрашенная часть?
Разделим каждую из долей еще на две части. (обращаю внимание на экран, где нарисован круг, разделенный на четыре части, две из которых закрашены)
Сколько долей получаем? Сколько из них заштриховано? Какой обыкновенной дроби соответствует полученный рисунок? Что вы заметили? Какие дроби по величине мы с вами получили? Какой знак между дробями мы можем с вами поставить? Мы получили, что одну и ту же часть круга можно записать в виде разных дробей, которые будут равны. Как вы думаете, возможно ли с помощью математических действий доказать, что эти дроби равны? Записываю на доске 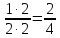
Какой вывод мы можем сделать?
Верно ли то, что вы только что сказали? Вы знаете, что умножить на два — это значит, что мы складываем две одинаковых части, если мы сложим две половинки, то что мы получим? Разве мы получили целое? Что же мы с вами делаем с дробью  , чтобы получить , чтобы получить 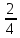 ? ? Для получения дроби равной данной надо числитель и знаменатель умножить на одно и то же число Как вы думаете, как нам из дроби 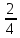 получить дробь получить дробь  ? ? Для получения дроби равной данной мы можем числитель и знаменатель разделить на одно и то же число Скажите пожалуйста, а может ли число, на которое мы будем делить равно нулю?
| У дробей одинаковые знаменатели, значит больше та дробь у которой больше числитель; 74, значит 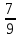  . . У дробей одинаковые числители, значит больше та дробь, у которой меньше знаменатель, 7  У этих дробей разные числители и знаменатели. Мы не умеем их сравнивать.
Сравнивать дроби с разными числителями и знаменателями
Научиться сравнивать дроби с разными числителями и знаменателями Работают с раздаточным материалом.
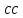

Четыре Две 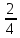
Половина круга и две четверти равны Равные
Равно
Да Если 1 ∙ 2 и 2 ∙ 2, то получим дробь  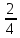
Мы дробь  умножаем на два и получаем умножаем на два и получаем  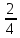 Да
Целое
Нет, мы получили 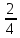 Мы умножили числитель и знаменатель на два.
Надо числитель и знаменатель разделить на два
Нет, на ноль делить нельзя. | Анализ, алгоритм исследования (методы математической науки)
Синтез
| Самоконтроль (контроль за исполнением алгоритма)
Самоконтроль (контролируем сбор всего необходимого и отбрасываем ненужное) | Проговаривание порядка действий
Формулировка определение понятия или правила, алгоритма |
| Применение понятия(правила) на новом материале Цель: закрепление понимания нового понятия (правила), применение правила (понятия) | Представьте данные дроби в виде дробей со знаменателем 12:  ; ;  ; ;  ; ;  ; ;  . . 1 человек у доски
Какое действие мы используем для того, чтобы получить дробь со знаменателем 12? 1 человек у доски
Какое действие мы используем для того, чтобы получить дробь со знаменателем 12? Такое преобразование называется сокращением дроби. Рассмотрим задание 346 стр.100. Прочитайте задание и подумайте, какое действие необходимо выполнить? Проговариваем, на какое число необходимо разделить числитель и знаменатель.
Как мы будем называть такое преобразование? Каким свойством дроби мы пользовались?
Как вы думаете, для чего мы сокращаем дроби? Как вы думаете, где можно применить это свойство дроби в жизни?
| 
Умножаем числитель и знаменатель на 3 
Умножаем числитель и знаменатель на 4  Умножаем числитель и знаменатель на 2 Умножаем числитель и знаменатель дроби на одно и то же число. 
Делим числитель и знаменатель на 2 
Делим числитель и знаменатель на 10 Делим числитель и знаменатель дроби на одно и то же число
Деление
Первую дробь на 3, получаем  Вторую дробь на 5, получаем  Третью дробь на 8, получаем  Четвертую дробь на 3, получаем  Сокращение дроби
Основным свойством дроби. Если числитель и знаменатель разделить на одно и то же число, не равное нулю, то мы получаем равную дробь. Чтобы числа были меньше
Масштаб (показывает во сколько раз уменьшено изображение, выражается в виде дроби) В науке, при многочисленных сложных вычислениях. | Применение признаков понятия | Коррекция признаков (существенных и несущественных) | Уточняем формулировку понятия |
| Итог урока Цели: закрепление алгоритма языкового разбора | Для того, чтобы вы убедились в том, что справитесь с домашней работой, выполним небольшую самостоятельную работу (с самопроверкой)
Сверяют с ответами, которые отображаются на экране. Исправляют ошибки. | Выполняют задания по вариантам 1вариант 1.Представьте данную дробь со знаменателем 3  . . 2.Среди данных дробей выберете те, которые равны дроби   , ,  , ,  . . 3.Сократите дробь :  , ,  , ,  . . 2вариант 1. Представьте данную дробь со знаменателем 5  . . 2. Среди данных дробей выберете те, которые равны дроби   , ,  , ,  . . 3. Сократите дробь :  , ,  , ,  . . | Рефлексия Восстановить ход нашего рассуждения, понятия | Самооценка Выработка критериев оценивания (зависит от активности формирования понятия) | Формулировка алгоритма, способа исследования |






 ;
;  и
и 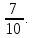
 и
и 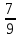
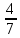
 и
и 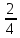 (создание проблемной ситуации)
(создание проблемной ситуации)