| I Организац. момент
| Положительный, эмоциональный настрой: Девиз нашего урока «Есть в математике нечто, вызывающее восторг» . На уроках геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур. Так вот, давайте сегодня на уроке будем следовать этой установки, будем активны, внимательны, развивать и тренировать свое геометрическое зрение.
| Концентрация внимания, положительный настрой на работу (Слайд 1) |
| Коммуникативные: доброжелательное отношение к окружающим. | Наличие чертежных инструментов, настрой на урок.
|
| II Повторение. Актуализация опорных знаний
| В 9 классе на экзамене ОГЭ есть такие задания, где нужно выбрать верные или неверные утверждения, давайте проверим, а сможем ли мы выполнить такое задание.
– Что вы знаете о геометрической фигуре?
Фронтальная беседа - определение треугольника; - какие треугольники вы знаете?
Что ещё мы знаем о треугольниках
|
Высказывания детей.
Отвечают на вопросы, делают выводы. (Умеем находить периметр треугольника, знаем признаки равенства треугольников, умеем строить и обозначать треугольники, знаем что сумма всех углов в треугольнике равны 180 и тд..)
Слайд 3 Классификация треугольников по углам и сторонам. (чертят треугольники у доски)
| Беседа | Коммуникативные: -умение выражать свои мысли; -отстаивать свою точку зрения. Регулятивные: -выдвигать версии; -прогнозировать. Познавательные: -сопоставлять характеристики объектов по одному или нескольким признакам; - выявлять сходство и различие объектов. |
Формирование у учащихся умения отбирать нужную информацию. |
| III. Изучение нового материала.
| Сегодня урок – исследование. Научиться исследовать, значит самостоятельно узнавать новое. Направляет работу учащихся, помогает найти нужную информацию.
Проверят усвоение прочитанного.
Организует практическую работу.
Подводит ребят к выдвижению гипотезы. Проверили опытным путем только на трех треугольниках.
Математика наука точная, чтобы утверждать, надо доказать. Еще Леонардо да Винчи говорил « Ни одно человеческое исследование не может назваться истинной наукой, если оно не прошло через математические доказательства» Физкультминутка.
Координирует, направляет работу учащихся при доказательстве свойства.
Наше предположение подтвердилось строгим доказательством.
На столах имеются тексты с исторической справкой о истории открытия равнобедренного треугольника. На доске имеется портрет Фалеса Милетского.
| 1.Читают п.18, стр. 35 и находят ответы на вопросы. Слайд 5. Какой треугольник называется равнобедренным? Как называются равные стороны? Как называется третья сторона треугольника?
2.Называют боковые стороны и основание изображенных треугольников Слайд 6. (изображение различных равнобедренных треугольников).
3.Практическая работа. На столе имеются треугольники трех цветов. Измеряют углы при основании этих треугольников и заполняют таблицу. | Углы | Красный Треугол. | Желтый Треугол. | Синий Треугол. | | Угол А | 300 | 450 | 700 | | Угол С | 300 | 450 | 700 |
Формулируют гипотезу. 4.Гипотеза. Слайд 5. У равнобедренного треугольника углы при основании равны.
5.Доказывают гипотезу.    С Дано: С Дано:
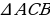 –равнобедрен. –равнобедрен. Доказать:     А = В А = В
А В Доказательство: 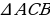 – равнобедренный, значит – равнобедренный, значит СА = СВ СВ = СА       С – общий, значит С – общий, значит 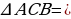 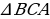 по первому признаку равенство треугольников, следовательно А= В по первому признаку равенство треугольников, следовательно А= В
6.Читают текст «О равнобедренном треугольнике. Фалес Милетский». Отвечают на вопросы: 1.В какой стране развивалось учение о треугольниках? 2.Какой ученый занимался изучением равнобедренного треугольника? 3.Научные достижения Фалеса Милетского. 4. Как Фалес доказал свойство равнобедренного треугольника? | Работа с текстом учебника
Фронтальная работа с классом.
Практическ. работа, работа в группах.
Беседа.
Работа у доски и в тетрадях
Работа с текстом
| Предметные: Научиться находить равнобедренные треугольники. Познавательные: -читать и извлекать нужную информацию; -умение работать с текстом. Коммуникативные: -умение точно и полно излагать свои мысли. Предметные: Научиться находить боковые стороны и основание треугольников.
Познавательные: -умение работать с транспортиром; -представлять информацию в виде таблиц. Коммуникативные: -умение выслушивать членов команды, не перебивая; принимать коллективные решения. Личностные: -формирование навыков коллективного проектирования.
Регулятивные: -формулировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций.
Познавательные: -читать и извлекать нужную информацию; -умение работать с текстом. Познавательные: - умения перерабатывать полученную информацию, делать выводы в результате индивидуальной работы. | Определение равнобедренного треугольника, боковые стороны и основание равнобедренного треугольника, равносторонний треугольник.
Таблица на доске и в тетрадях.
Запись гипотезы в тетрадях.
Доказательство гипотезы в тетрадях. |
| IV Решение практических задач (закрепление пройденного материала). | 1.Организует работу в группах. Любое исследование должно иметь практическое применение.
Направляет работу учащихся.
Запишите в тетрадях главный вывод задачи.
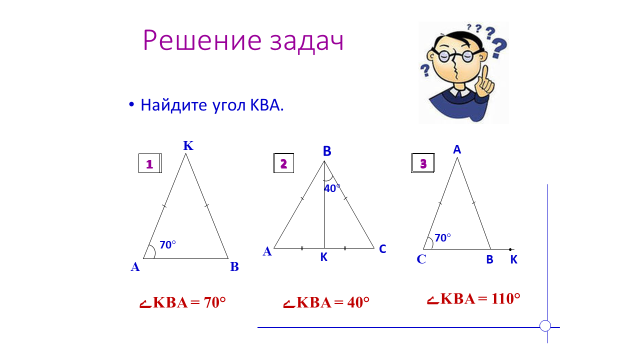
| 7. Решают практические задачи на готовых чертежах. Найти угол КВА. 
8. В равнобедренном треугольнике боковая сторона равна 9 см, а основание 5см. Вычислите периметр треугольника. В равнобедренном треугольнике основание равно 7см, а периметр равен 17см. Вычислите боковую сторону треугольника. В равностороннем треугольнике периметр равен 21см. Вычислите сторону треугольника.
8.Работа над задачей №109, стр.37 учебник. Самостоятельный разбор задачи. | Устная работа над задачами
Индивидуальная работа учащихся. | Коммуникативные: - умение оформлять свою мысль в учебной речи; - грамотно формулировать высказывания. Предметные: -научиться применять теорему о свойствах углов равнобедренного треугольника. Регулятивные: - умения выполнять учебные действия в соответствии с планом.
|
Применение знаний на практике.
Записи в тетрадях |
| V. Проверка изученного. | Мы славно потрудились на уроке, узнали много нового. Хотелось бы узнать, как вы усвоили материал урока. У меня в руках два листа бумаги. На одном изображен разносторонний треугольник, а на другом равнобедренный. Задайте мне только один вопрос и выслушав ответ, скажите, какой треугольник на каком листе изображен? | 9. Задают вопросы. | Индивидуальная работа учащихся. | Познавательные: -уметь устанавливать причино-следственные связи. |
|
| VII. Итог урока и домашнее задание.
| 1.Комментирует домашнее задание | Записывают домашнее задание. п. 18, № 112, 115. Ответить на вопрос «Где встречаются равнобедренные треугольники в жизни?» |
| Познавательные: - находить ответы, используя свой жизненный опыт и информацию, полученную на уроке. |
|







 С Дано:
С Дано: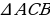 –равнобедрен.
–равнобедрен.


 А = В
А = В



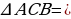
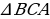 по первому признаку равенство треугольников, следовательно А= В
по первому признаку равенство треугольников, следовательно А= В 
 СТОРИЧЕСКАЯ СПРАВКА ОБ ИСТОРИИ ОТКРЫТИЯ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
СТОРИЧЕСКАЯ СПРАВКА ОБ ИСТОРИИ ОТКРЫТИЯ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА











