| Цели деятельности учителя | Создать условия для введения понятий равнобедренного треугольника, равностороннего треугольника, рассмотрения свойств равнобедренного треугольника и демонстрации их применения на практике |
| Термины и понятия | Равнобедренный треугольник, равносторонний треугольник, боковые стороны, основание, углы при основании |
| Планируемые результаты |
| Предметные умения | Универсальные учебные действия |
| Владеют базовым понятийным аппаратом по основным разделам содержания; имеют представление об основных изучаемых понятиях как важнейших геометрических моделях, позволяющих описывать и изучать реальные математические процессы и явления | Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение; понимают и используют математические средства наглядности. Регулятивные: осознают и принимают цели и задачи учебной деятельности. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
| Организация пространства |
| Формы работы | Фронтальная (Ф); индивидуальная (И); групповая (Г) |
| Образовательные ресурсы | -
Геометрия. 7 – 9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. – М.: Просвещение, 2023. -
Задания для самостоятельной работы |
| I этап. Актуализация опорных знаний учащихся |
| Цель деятельности | Совместная деятельность |
| Проверить правильность выполнения домашнего задания | (Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию. 2. Теоретический опрос учащихся. 3. Самостоятельное решение тестовых заданий с последующей самопроверкой: 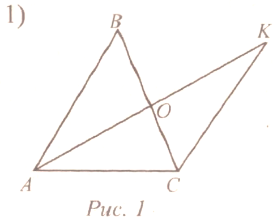
Дано: АО – медиана АВС, АО = ОК, АВ = 6,3 см, ВС = 6,5 см, АС = 6,7 см. Найти: СК. а) 6,4 см; б) 6,7 см; в) 6,5 см; г) 6,3 см.
Д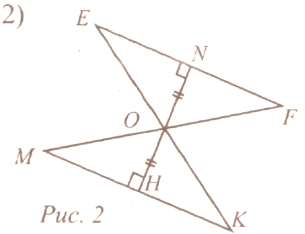 ано: ОН и ОN – высоты МОК и ЕОF, OH = ON, EN = 7,8 см, ОЕ = 8,6 см, HM = 6,3 см. ано: ОН и ОN – высоты МОК и ЕОF, OH = ON, EN = 7,8 см, ОЕ = 8,6 см, HM = 6,3 см. Найти: МК. а) 13,9 см; б) 14,1 см; в) 14,9 см; г) 16,4 см.
3) В треугольниках АВС и КРМ проведены биссектрисы ВО и РЕ, причем АОВ = КРЕ. Найдите отрезок ЕМ, если АС = 9 см, а ЕМ больше КЕ на 3,8 см. а) 6,4 см; б) 5,4 см; в) 2,6 см; г) 4,8 см. Ответы: 1 – г; 2 – б; 3 – а |
| II этап. Учебно-познавательная деятельность |
| Цель деятельности | Совместная деятельность |
| Ввести понятия равнобедренного и равностороннего треугольников, дать представления о свойствах равнобедренного треугольника | (Ф/И) 1. Понятия равнобедренного и равностороннего треугольников. Определение: Треугольник, две стороны которого равны, называется равнобедренным. Равные стороны называются боковыми сторонами, а третья сторона – основанием равнобедренного треугольника. На доске и в тетрадях – рисунок и запись: АВС – равнобедренный, так как АВ = ВС; АВ, ВС – боковые стороны равнобедренного АВС; АС – основание равнобедренного АВС; А, С – углы при основании равнобедренного АВС; В – угол при вершине равнобедренного АВС. 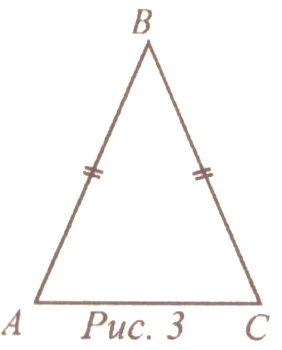
Определение: Треугольник, все стороны которого равны, называется равносторонним. 2. Свойство углов при основании равнобедренного треугольника. Теорема: В равнобедренном треугольнике углы при основании равны. Д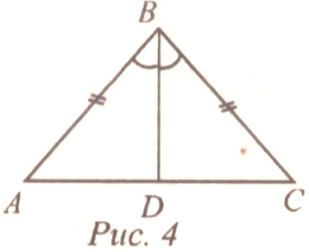 ано: АВС, АВ = ВС. ано: АВС, АВ = ВС. Доказать: А = С.
Доказательство: Проведем биссектрису из вершины В к основанию АС. (Далее можно предложить доказательство самостоятельно, заслушать варианты, обсудить и записать в кратком виде ход доказательства.) (Г) 3. Свойство биссектрисы, проведенной к основанию равнобедренного треугольника. Можно предложить учащимся вывести это свойство самостоятельно, поставив перед ними проблему: «Как известно, биссектриса треугольника делит его угол пополам. Но в равнобедренном треугольнике биссектриса, проведенная к основанию, обладает еще одним очень важным свойством. В чем заключается это свойство?» Работа проводится в группах по 3-4 человека с последующим обсуждением этого свойства с доказательством. При обсуждении важно затронуть вопросы: – Каждая ли биссектриса равнобедренного треугольника является его высотой и медианой? – Является ли высота равнобедренного треугольника его биссектрисой и медианой? Если да, то какая из трех?
|
| III этап. Творческое задание |
| Цель деятельности | Задания для самостоятельной работы |
| Способствовать исследованию свойств медиан и высот равнобедренного треугольника в ходе выполнения заданий творческого характера | (И) Вариант I Исследуйте медианы равнобедренного треугольника и перечислите все их особенности и свойства. Вариант II Исследуйте высоты равнобедренного треугольника и перечислите все их особенности и свойства. Далее проходит обсуждение свойств медианы и высоты равнобедренного треугольника
|
| IV этап. Решение задач |
| Цель деятельности | Деятельность учителя | Деятельность учащихся |
| Совершенствовать навыки решения задач на применение изученных фактов | (Ф/И) 1. Решить задачи № 113 и 117 на доске и в тетрадях. 2. Решить № 121 (устно). 3. Решить задачу (устно). В равнобедренном треугольнике сумма всех углов равна 180. Найдите углы этого треугольника, если известно, что: а) один из них равен 105; б) один из них равен 38(рассмотреть два случая)
| № 113.  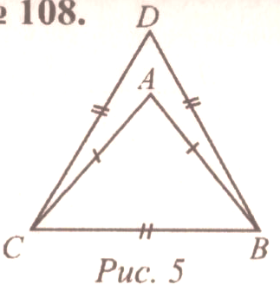
Дано: ABС, АВ = АС, РАВС = 40 см, ВCD, DВ = DС = ВС, РВСD= 45 см. Найти: АВ и ВС.
Решение: 1) РАВС = АВ + ВС + АС = ВС +2АВ (так как ABС равнобедренный) 40 = ВС + 2АВ. 2) РВCD = DB + ВС + СD = 3ВС (так как ВCD равносторонний) 45 = 3ВС, тогда ВС = 15 см. 40 = 15 + 2АВ 2АВ = 25, тогда АВ = 12,5 см Ответ: 12,5 см, 15 см.  №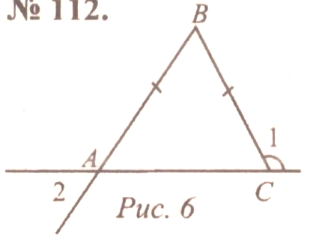 117. 117.
Дано: АВ = ВС, 1 = 130. Найти: 2.
Решение: 1) 1 и АСВ – смежные, значит, 1 + АСВ = 180, тогда АСВ = 180 – 130 = 50. 2) Так как АВС – равнобедренный, АВ = ВС (по усл.), то ВАС = ACВ = 50. 3. Так как 2 = ВАC, как вертикальные, то 2 = 50. Ответ: 50 |
| IV этап. Итоги урока. Рефлексия |
| Деятельность учителя | Деятельность учащихся |
| (Ф/И) – Что узнали об углах равнобедренного треугольника? Равностороннего треугольника? – Перечислите свойства равнобедренного и равностороннего треугольников. – Задайте три вопроса по теме урока | (И) Домашнее задание: изучить п. 18 с доказательством теоремы об углах при основании равнобедренного треугольника; ответить на вопросы 10-13 на с. 49 учебника; решить задачи № 109, 112 и 122 |








 ано: ОН и ОN – высоты МОК и ЕОF, OH = ON, EN = 7,8 см, ОЕ = 8,6 см, HM = 6,3 см.
ано: ОН и ОN – высоты МОК и ЕОF, OH = ON, EN = 7,8 см, ОЕ = 8,6 см, HM = 6,3 см.
 ано: АВС, АВ = ВС.
ано: АВС, АВ = ВС.


 117.
117.


















