| Здравствуйте! Этими словами мы желаем друг другу самого главного – здоровья, а все остальное приложится. Сегодня мы проведем необычный урок – урок «Право на ошибку». Почему? – спросите вы. Людям свойственно ошибаться, не ошибается лишь тот, кто ничего не делает. А эпиграфом нашей работы будут слова Карла Поппера, австрийского философа, логика, социолога: «Я могу ошибаться, и ты можешь ошибаться, но совместными усилиями мы можем постепенно приближаться к истине» 1. Сначала, мы вместе восхитимся глубокими знаниями – а для этого проведем небольшую устную работу. 2. Потом попробуем ответить на вопрос в чем суть первого признака подобия треугольников. 3. Затем потренируем мозги – порешаем задачи, достанем из тайников памяти что-то ценное.
1. В треугольнике АВС угол А равен углу С. Найдите угол С, если угол В равен 85º.
Что можно сказать об углах треугольника?
Можем ли мы найти градусную меру угла С? Как?
Чему равен угол С? Запишем ответ.
|
Сумма углов треугольника равна 180º.
Для того, чтобы вычислить градусную меру угла С, надо из 180º вычесть градусную меру угла В, и полученный результат разделить на 2, т.к. С = А по условию
Угол С равен 47º30’.
|
«Я могу ошибаться, и ты можешь ошибаться, но совместными усилиями мы можем постепенно приближаться к истине» Карл Поппер, австрийский философ, логик, социолог.
Сегодня на уроке: 1. Устная работа (повторение теоремы о сумме углов треугольника, определение подобных треугольников, отношение их сторон, отношение площадей). 2. Первый признак подобия треугольников (формулировка, доказательство). 3. Решение задач (применение признака подобия треугольников).
|  В В
А С Дано:∆АВС, А = С, В = 85º. Найти: С. Решение: А + С + В = 180º А + 85º + С = 180º А + С = 180º -  85º 85º А + С = 2 С 2 С = 180º - 85º 2 С = 95º С = 95º: 2 С = 47º30’
Ответ: С = 47º30’
|
|
|
2. В подобных треугольниках АВС и EFD стороны АВ и EF, ВС и FD являются сходственными. Найдите стороны ∆ EFD, если АВ = 4 см, ВС = 5 см, СА = 7 см,  = 2,1 = 2,1
Можем ли мы найти стороны ∆ EFD? Как?
Можем ли мы определить стороны ∆ EFD из этого следствия? Попробуйте определить самостоятельно.
Чему равны стороны ∆ EFD? Запишем ответ. |
Да. Из определения подобных треугольников следует, что  = = 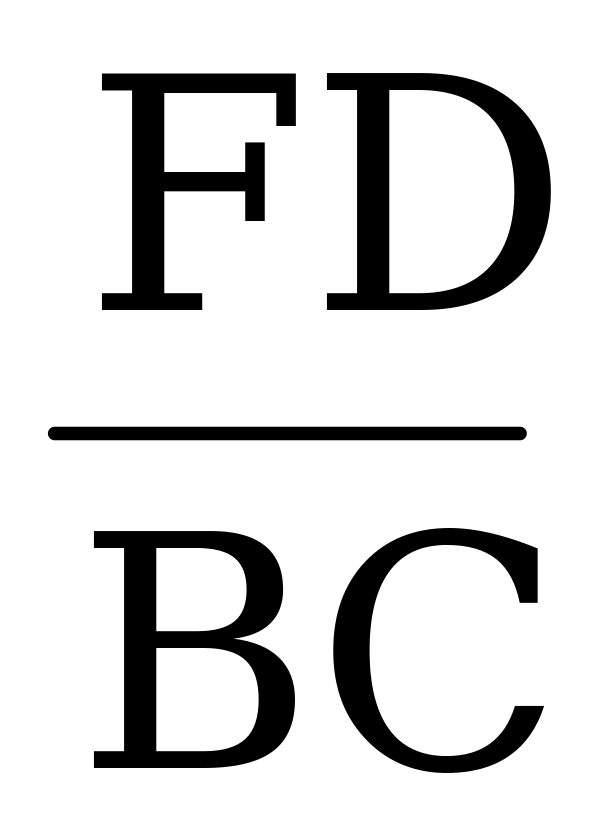 = = 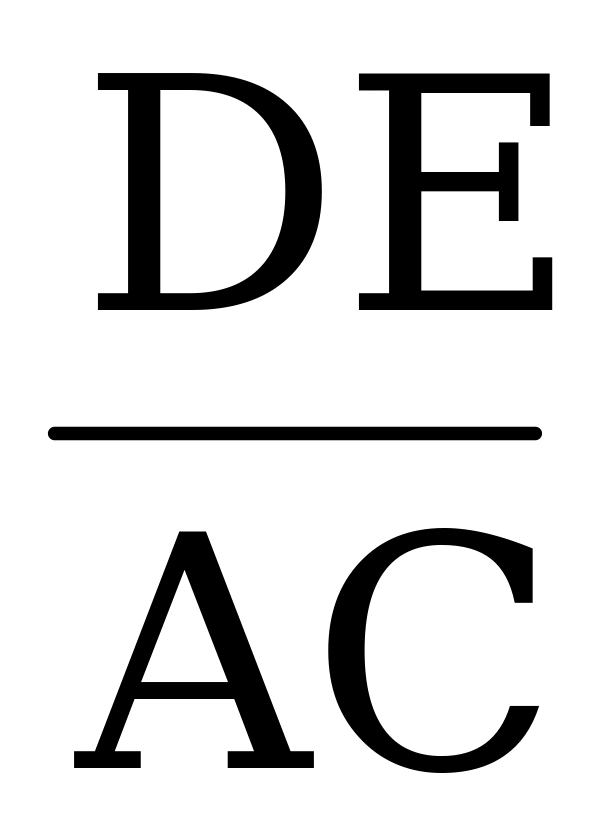 = k, где k = 2,1. = k, где k = 2,1.
Определяют.
EF = 8,4 см; FD = 10,5 см; DE = 14,7 см. |  
А F В
E С D
Дано: ∆ EFD ~ ∆ АВС, АВ и EF, ВС и FD – сходственные, АВ = 4 см, ВС = 5 см, СА = 7 см, ~ ∆ АВС, АВ и EF, ВС и FD – сходственные, АВ = 4 см, ВС = 5 см, СА = 7 см,  = 2,1. = 2,1. Найти: EF, FD, DE. Решение: Т.к. ∆ EFD ~ ∆ АВС, то ~ ∆ АВС, то  = = 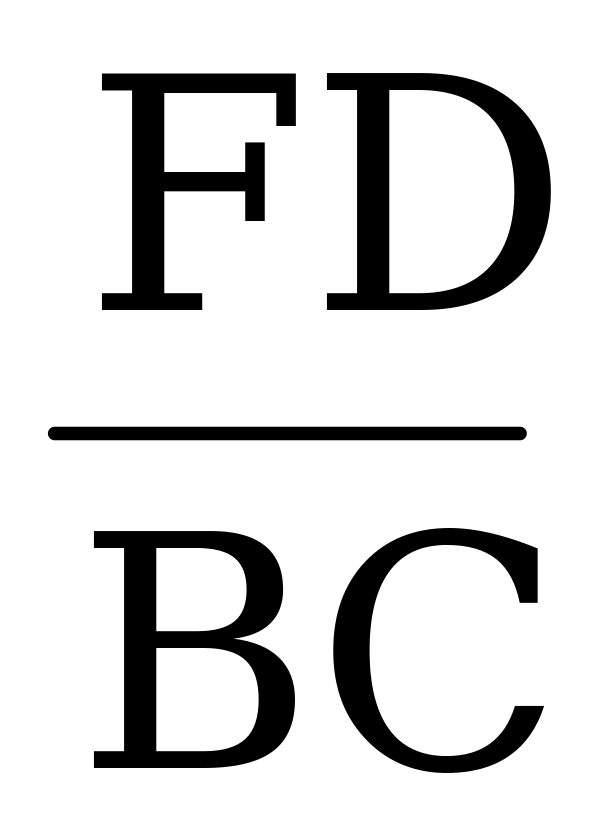 = = 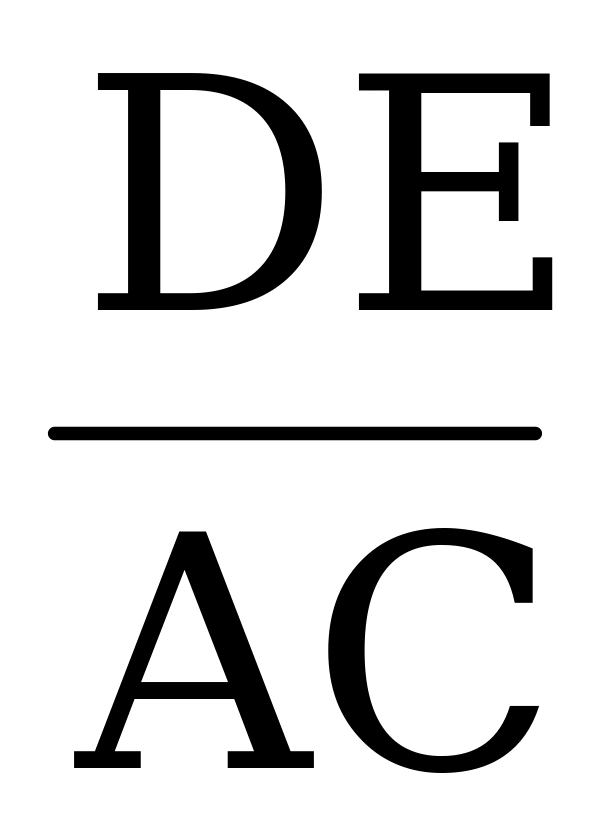 = k, где k = 2,1. = k, где k = 2,1.
 = 2,1; = 2,1; 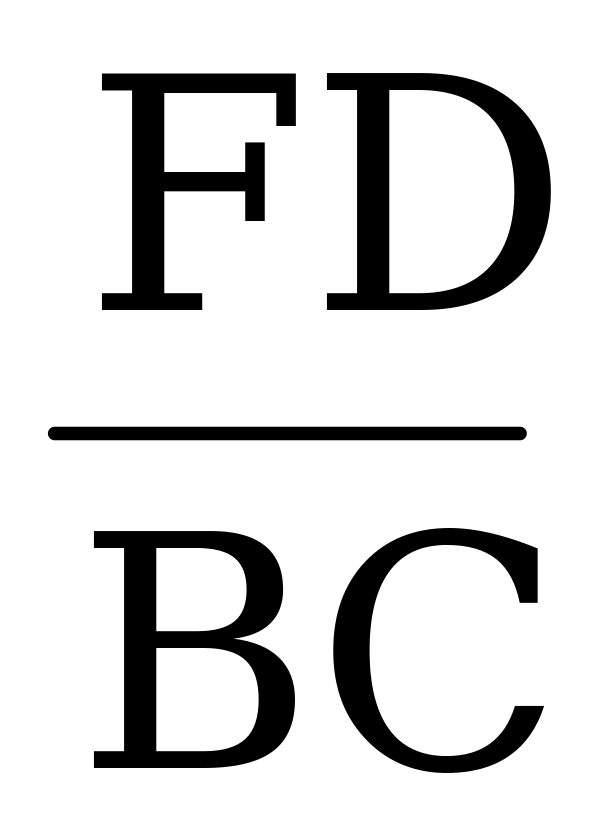 =2,1; =2,1; 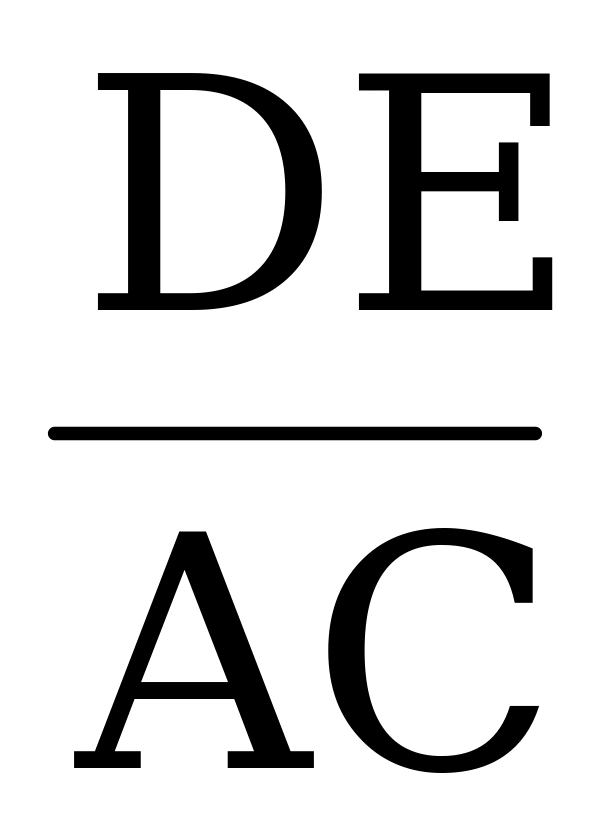 =2,1. =2,1. 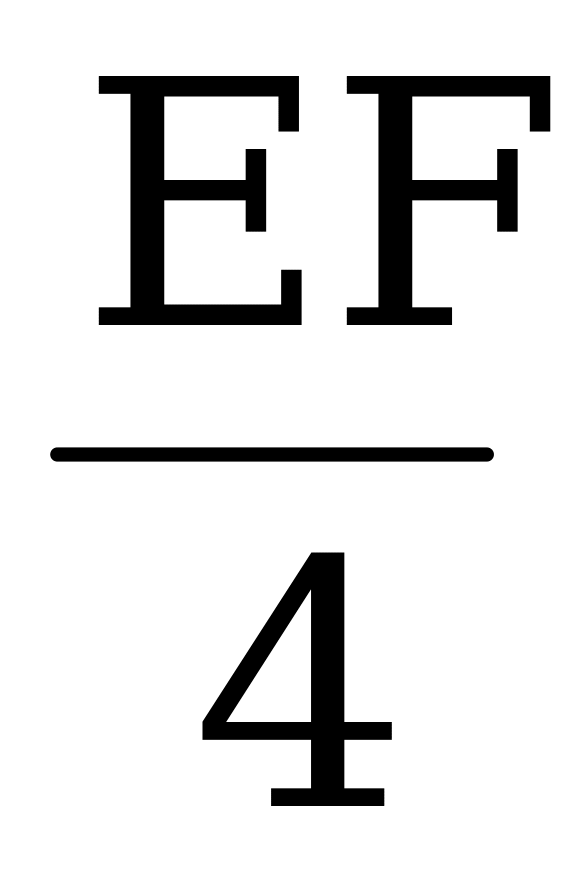 = 2,1; EF = 4 · 2,1 = 8,4 см. = 2,1; EF = 4 · 2,1 = 8,4 см.  =2,1; FD = 5 · 2,1 = 10,5 см. =2,1; FD = 5 · 2,1 = 10,5 см.  =2,1; DE = 7 · 2,1 = 14,7 см. =2,1; DE = 7 · 2,1 = 14,7 см.
Ответ: EF = 8,4 см; FD = 10,5 см; DE = 14,7 см. |
|
3. Площади двух подобных треугольников равны 75 см² и 300 см². Одна из сторон второго треугольника 9 см. Найдите сходственную ей сторону первого треугольника.
Запишем условие задачи. Что говориться о треугольниках?
Запишем дано, обозначив треугольники ABC и MNK. За площадь первого треугольника примем площадь MNK, второго – ABC.
Как можно узнать сторону первого треугольника сходственную стороне второго треугольника?
Покажите это на рисунке.
Какой вывод можно сделать?
Запишите это.
Чему равно отношение площадей и как это записать?
Как можно определить коэффициент подобия, зная площади треугольников. Определите.
Что мы можем узнать зная коэффициент подобия? Как?
Можем ли мы узнать сторону MN треугольника MNK? Запишите как.
Запишите ответ. |
У двух подобных треугольников площади равны 75 см² и 300 см², одна из сторон второго треугольника 9 см.
Если наложить один треугольник на другой таким способом, чтобы сходственные стороны совпали, то одна вершина у них будет общая.
Отношение площадей треугольников равно произведению отношений его сторон, принадлежащих общей вершине треугольников.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Надо извлечь квадратный корень из отношения площадей треугольников.
Отношение сторон треугольников.  = =  = =  = k = k
Если рассмотреть одно из отношений  = k, то можно найти сторону MN. = k, то можно найти сторону MN.
|
Площади двух подобных треугольников равны 75 см² и 300 см². Одна из сторон второго треугольника 9 см. Найдите сходственную ей сторону первого треугольника.

A
B
C M N
K
Дано: ∆ MNK ~ ∆ АВС, AB = 9 см, S1 = 75 см², S2 = 300 см². Найти: MN. Решение:
B  N
A M K C
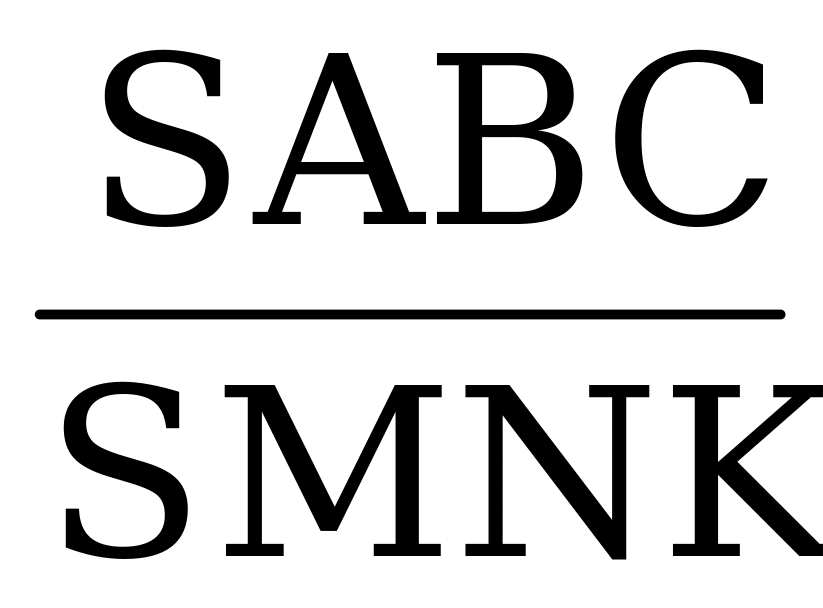 = = 
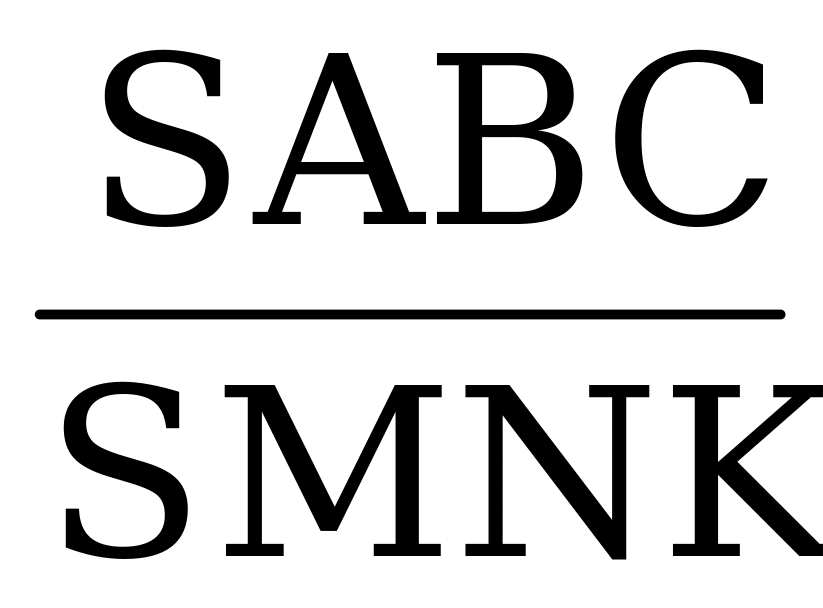 = k² = k²
 = k²; k = = k²; k =  ; k = 2 ; k = 2
 = =  = =  = k = k
 = k; MN = 9 : 2 = 4,5 см = k; MN = 9 : 2 = 4,5 см
Ответ: MN = 4,5 см.
|
|
Как можно ли убедится в том, что ∆ DFE = ∆ АВС?
Можно ли убедится в том, что ∆ DFE = ∆ АВС, если бы А = D, B = F?
Как вы думаете, что можно сказать о ∆ DFE и ∆ АВС? Почему?
Вспомните определение подобных треугольников.
Достаточно ли того, что в треугольниках равны два соответственных углах, чтобы убедится в том, что треугольники подобны?
Попробуйте сформулировать признак подобия треугольников по двум углам.
Попробуем восстановить ход доказательства задачи и определим план доказательства.
А теперь докажем сам признак подобия треугольников.
Оформляем теорему: Чему равен угол С ∆ АВС? Угол С1 ∆ А1В1С1?
Что можно сказать об отношении площадей треугольников?
Используя равенство отношений площадей и сторон, можем доказать, что сходственные стороны треугольников пропорциональны.
Мы доказали, что ∆ АВС ~ ∆ А1В1С1
Долго тянется урок Много вы решали Не поможет тут звонок Раз глаза устали Занимаемся все сразу Повторим четыре раза.
В качестве тренажера нам сегодня послужит знак подобия.
Пройдите глазами по знаку подобия. Закройте глаза. Расслабьтесь. Медленно переведите глаза в крайнее левое положение. Зафиксируйте положение. Переведите медленно положение глаз вправо. Зафиксируйте положение. Откройте глаза. Пройдите глазами по знаку подобия. Быстро моргните четыре раза.
|
Если при наложении одного треугольника на другой, треугольники полностью совместятся, то треугольники равны.
Нет.
Треугольники ∆ DFE и ∆ АВС подобны, т.к. два угла одного треугольника соответственны двум углам другого, стороны одного треугольника сходны двум сторонам другого треугольника.
Два треугольника называют подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Да.
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
1. Нашли градусную меру угла С. 2. Определили сходные стороны, их пропорциональность. 3. Определили соотношение площадей треугольников.
Утверждение: 1. С = 180 - А - В С1 = 180 - А1 - В1
2.  = = 
 = = 
3.  = =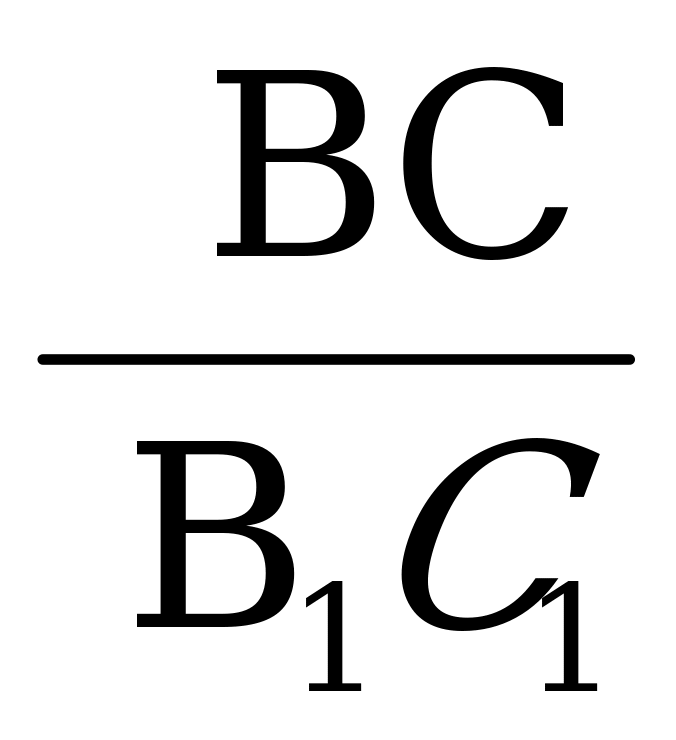
 = =
|
 
А F В
E С D
 A A A1 B1
B C C1
Дано: ∆ АВС и ∆ А1В1С1, А = А1, В = В1. Доказать: ∆ АВС ~ ∆ А1В1С1 Доказательство:
Обоснование: Теоремма о сумме углов треугольника.
Теорема о соотношении площадей треугольников.
3. Пропорциональность сходных сторон.
|
| Сформулируйте еще раз признак подобия треугольников.
Выделите условие.
Выделите заключение.
Сейчас я буду зачитывать утверждения, а вы ответьте верно ли оно и почему?
1. Если угол одного треугольника соответственно равен углу другого треугольника, то такие треугольники подобны.
2.Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
3.Если угол и сторона одного треугольника соответственно равны углу и стороне другого, то такие треугольники подобны.
Подумайте, будут ли подобны треугольники на рисунках. Почему?
Решите задачу: В треугольнике АВС угол А равен 48º, угол С равен 35º, а в треугольнике DEF угол Е равен углу А треугольника АВС. Проверьте, будут ли подобны треугольники, если угол D равен 97º.
Что надо знать, чтобы убедиться в подобии треугольников?
Есть ли у нас равные углы по условию задачи?
Можно ли найти вторую пару соответственно равных углов?
Можем ли мы найти градусную меру углов В и F? Как?
Рассмотрим треугольник АВС и найдем угол В самостоятельно.
Сравните угол В с углом D.
Что можно сказать о треугольниках теперь?
А сейчас каждая из вас составит свою задачу.
Выберите карточку по цвету, оценив свою работу на уроке: Красный – заслуживаю высокой оценки. Желтый – заслуживаю хорошей оценки. Зеленый – заслуживаю удовлетворительной оценки. Черный – не заслужила оценки.
Откройте дневники и запишите домашнее задание п. 49, вопрос 5, выполнить № 550, 551(а), 553, по желанию придумайте 2-3 своих задачи и решите их.
Совместными усилиями, к какой же истине мы пришли?
А в завершение нашей работы я хочу пожелать, чтобы ошибки, которые вы допускаете, не приводили вас к унынию, а являлись импульсом для саморазвития. | Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Два угла одного треугольника соответственно равны двум углам другого треугольника.
Такие треугольники подобны.
Неверно, т.к. признак подобия треугольников предусматривает равенство двух соответственных углов.
Верно, т.к. это формулировка признака подобия треугольников.
Неверно, т.к. признак предусматривает равенство двух соответственных углов, а не углов и сторон.
Рис.4-а. Треугольники подобны, т.к. угол А равен углу Е, угол В равен углу F, следовательно треугольники подобны по двум соответственно равным углам.
Рис.4-б. Треугольники не подобны, т.к. нет двух соответственно равных углов, а значит не выполняется признак подобия треугольников.
Для того, чтобы убедиться в подобии треугольников, нужно найти два соответственно равных угла.
Есть, угол А и угол Е.
Можно найти градусную меру угла В и проверить будет ли он равен углу Д; или найти градусную меру угла F и проверить будет ли он равен углу С.
Можно, используя теорему о сумме углов треугольника.
Самостоятельно находят угол В.
Угол В равен углу D.
Треугольники подобны по двум углам. Угол А равен углу E по условию, угол В равен углу D по решению.
Повторили определение подобных треугольников, отношение их сторон, теорему о сумме углов треугольника. Сформулировали признак подобия треугольников по двум углам и доказали его. Применили признак подобия треугольников к решению задач. |
 
Дано: ∆ EFD и ∆ АВС, А = Е = 48º, С = 35º, D = 97º
Доказать: ∆ EFD ~ ∆ АВС ~ ∆ АВС
Доказательство: рассм. ∆ АВС: А = 48º, С = 35º, В = ? А + С + В = 180º В = 180º - А - С В = 180º - 48º - 35º В = 97º = D А = Е = 48º - по усл.  ∆ EFD ~ ∆ АВС ~ ∆ АВС |







 В
В



 A
A


















