Вариант № 15





6. Найдите значение выражения 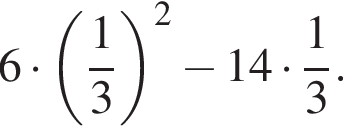
Решение. Вынесем общий множитель за скобки:
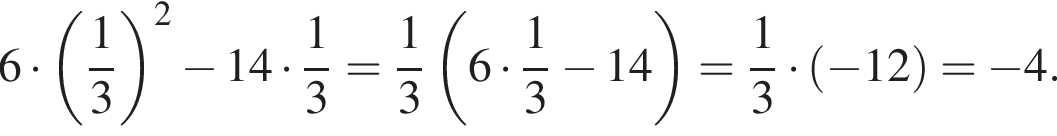
Ответ: −4.
7. О числах a, b, c и d известно, что  ,
,  ,
,  . Сравнитe числа d и a.
. Сравнитe числа d и a.
В ответе укажите номер правильного варианта.
1) 
2) 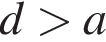
3) 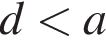
4) Сравнить невозможно
Решение. По условию  поэтому
поэтому 
Правильный ответ указан под номером 2.
8. Найдите значение выражения 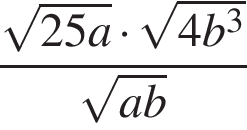 при a = 7 и b = 11.
при a = 7 и b = 11.
Решение. Упростим выражение:
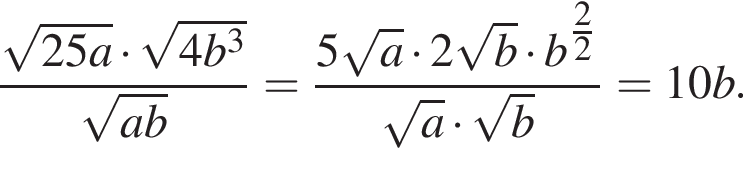
При b = 11 значение полученного выражения равно 10 · 11 = 110.
Ответ: 110.
9. Найдите корни уравнения 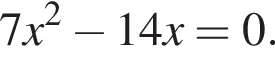
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение. Вынесем общий множитель за скобки:
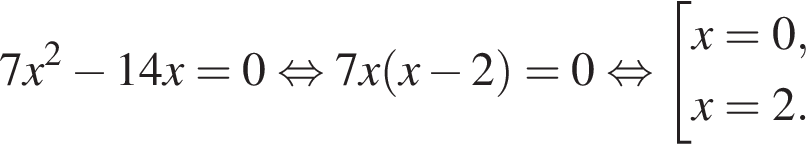
Ответ: 02.
10. Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
Решение. Вероятность события равна отношению количества благоприятных случаев к количеству всех случаев. Благоприятными случаями являются 3 случая, когда игру начинает Петя, Игорь или Антон, а количество всех случаев 6. Поэтому искомое отношение равно 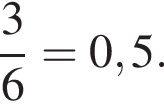
Ответ: 0,5.
11. Установите соответствие между графиками функций и формулами, которые их задают.
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
Решение. Напомним, что если парабола задана уравнением 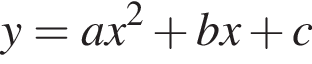 , то: при
, то: при  то ветви параболы направлены вверх, а при
то ветви параболы направлены вверх, а при  — вниз; абсцисса вершины параболы вычисляется по формуле
— вниз; абсцисса вершины параболы вычисляется по формуле 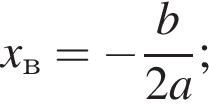 парабола пересекает ось Oy в точке с.
парабола пересекает ось Oy в точке с.
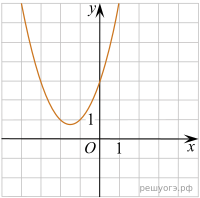
Уравнение 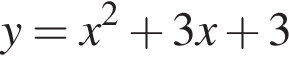 задает параболу, ветви которой направлены вверх, абсцисса вершины равна
задает параболу, ветви которой направлены вверх, абсцисса вершины равна  , она пересекает ось ординат в точке 3. Ее график изображен на рисунке А).
, она пересекает ось ординат в точке 3. Ее график изображен на рисунке А).
Уравнение 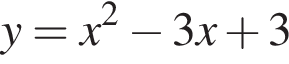 задает параболу, ветви которой направлены вверх, абсцисса вершины равна
задает параболу, ветви которой направлены вверх, абсцисса вершины равна 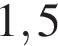 , она пересекает ось ординат в точке 3. Такого графика на рисунках нет.
, она пересекает ось ординат в точке 3. Такого графика на рисунках нет.
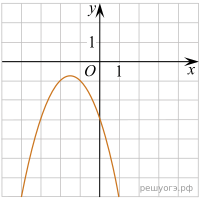
Уравнение 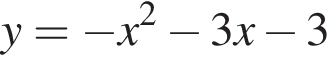 задает параболу, ветви которой направлены вниз, абсцисса вершины равна
задает параболу, ветви которой направлены вниз, абсцисса вершины равна  , она пересекает ось ординат в точке −3. Ее график изображен на рисунке Б).
, она пересекает ось ординат в точке −3. Ее график изображен на рисунке Б).
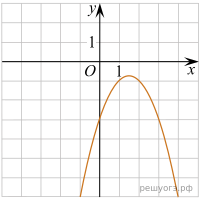
Уравнение 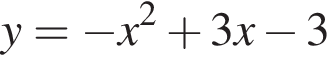 задает параболу, ветви которой направлены вниз, абсцисса вершины равна
задает параболу, ветви которой направлены вниз, абсцисса вершины равна 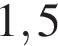 , она пересекает ось ординат в точке −3. Ее график изображен на рисунке В).
, она пересекает ось ординат в точке −3. Ее график изображен на рисунке В).
Тем самым, искомое соответствие: А—1, Б—3, В—4.
Ответ: 134.
12. Площадь четырёхугольника можно вычислить по формуле 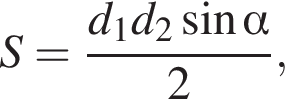 где
где 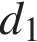 и
и 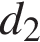 — длины диагоналей четырёхугольника,
— длины диагоналей четырёхугольника, 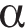 — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали 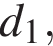 если
если 
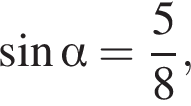 a
a 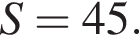
Решение. Выразим длину диагонали 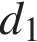 из формулы для площади четырёхугольника:
из формулы для площади четырёхугольника:
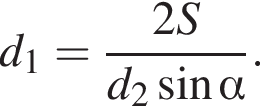
Подставляя, получаем:
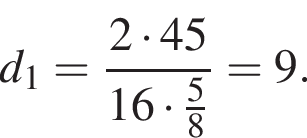
Ответ: 9.
13. Укажите решение системы неравенств
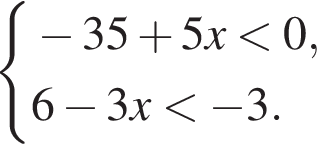
| 1) 
| 2) нет решений |
| 3) 
| 4) 
|
Решение. Решим систему:
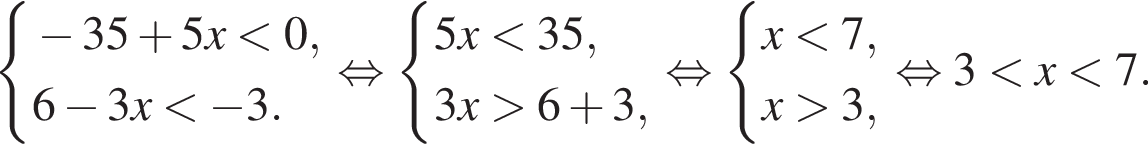
Ответ: 1.
14. Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке 22 минуты, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на 4 минуты, пока оно не достигнет 60 минут, а дальше продолжать тренироваться по 60 минут каждый день. За сколько занятий, начиная с первого, Андрей проведёт на беговой дорожке в сумме 4 часа 48 минут?
Решение. Время, проведённое на беговой дорожке представляет собой арифметическую прогрессию с первым членом равным 22 и разностью 4. Сумма n членов арифметической прогрессии может быть найдена по формуле:
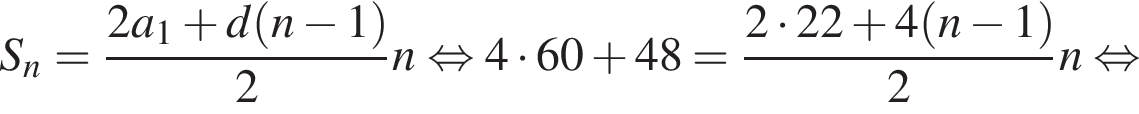
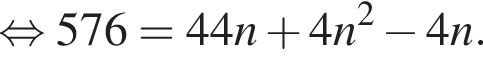
Получили квадратное уравнение на n, решим его:
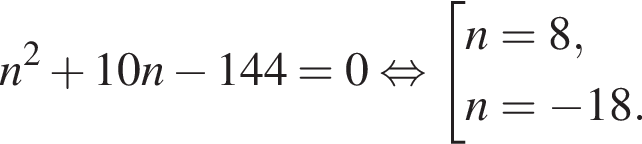
По условию задачи подходит значение 8.
Ответ: 8.
Примечание.
Заметим, что в восьмой день Андрей проведет на беговой дорожке 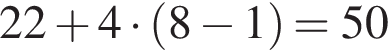 минут, то есть меньше 60 минут. Заметим также, что если в первый день время тренировки составило 22 минуты и увеличивается на 4 минуты в день, то оно никогда не станет равно 60 минутам: в девятый день время составит 54 минуты, в десятый день — 58 минут и в одиннадцатый день — 62 минуты.
минут, то есть меньше 60 минут. Заметим также, что если в первый день время тренировки составило 22 минуты и увеличивается на 4 минуты в день, то оно никогда не станет равно 60 минутам: в девятый день время составит 54 минуты, в десятый день — 58 минут и в одиннадцатый день — 62 минуты.
Приведем решение задачи подбором:
| день | время тренировки | суммарное время тренировок |
| 1 | 22 | 22 |
| 2 | 26 | 48 |
| 3 | 30 | 78 |
| 4 | 34 | 112 |
| 5 | 38 | 150 |
| 6 | 42 | 192 |
| 7 | 46 | 238 |
| 8 | 50 | 288 |
Таким образом, за 8 дней суммарное время тренировок достигнет 288 минут, или 4 часов 48 минут.
15.
Прямые m и n параллельны. Найдите ∠3, если ∠1 = 111°, ∠2 = 18°. Ответ дайте в градусах.
Решение.  Введём обозначение, как показано на рисунке. Углы 1 и 4 соответственные, поэтому ∠4 = ∠1 = 111°. Углы 2, 3 и 4 — это углы одного треугольника, сумма углов треугольника равна 180°, откуда ∠3 = 180° − 111° − 18° = 51°.
Введём обозначение, как показано на рисунке. Углы 1 и 4 соответственные, поэтому ∠4 = ∠1 = 111°. Углы 2, 3 и 4 — это углы одного треугольника, сумма углов треугольника равна 180°, откуда ∠3 = 180° − 111° − 18° = 51°.
Ответ: 51.
16.  Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 25. Найдите AC, если
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 25. Найдите AC, если 
Решение. Известно, что если центр описанной окружности лежит на стороне треугольника, то угол напротив этой стороны — прямой. Таким образом, угол C - прямой. Тогда по теореме Пифагора найдем AC:
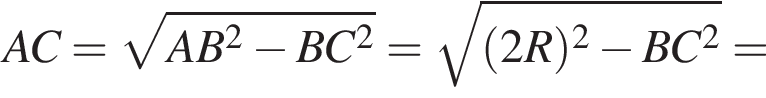
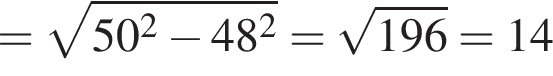
Ответ: 14
17.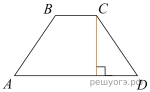
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 3. Найдите длину основания BC.
Решение. 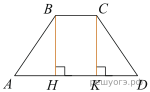 Проведём вторую высоту и введём обозначения, как показано на рисунке. Рассмотрим треугольники ABH и CKD, они прямоугольные, AB равно CD, BH равно CK, следовательно, эти треугольники равны, откуда
Проведём вторую высоту и введём обозначения, как показано на рисунке. Рассмотрим треугольники ABH и CKD, они прямоугольные, AB равно CD, BH равно CK, следовательно, эти треугольники равны, откуда  Найдём отрезок
Найдём отрезок 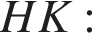
 Высоты BH и CK перпендикулярны AD, значит, они параллельны, BH равно CK, следовательно, HBCK — прямоугольник, поэтому
Высоты BH и CK перпендикулярны AD, значит, они параллельны, BH равно CK, следовательно, HBCK — прямоугольник, поэтому 
Ответ: 2.
18.
Найдите тангенс угла, изображённого на рисунке.
Решение. 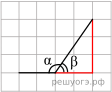 Углы
Углы 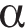 и
и  в сумме образуют развёрнутый угол
в сумме образуют развёрнутый угол  Значит,
Значит, 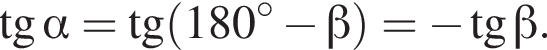
Рассмотрим прямоугольный треугольник, изображённый на рисунке. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
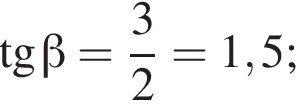

Ответ: -1,5.
19. Какое из следующих утверждений верно?
1. Все квадраты имеют равные площади.
2. Основания равнобедренной трапеции равны.
3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
В ответ запишите номер выбранного утверждения.
Решение. Рассмотрим каждое из утверждений:
1. Все квадраты имеют равные площади - неверно, так как длины сторон могут отличаться.
2. Основания равнобедренной трапеции равны - неверно.
3. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности - верно.
Ответ: 3
20. Упростите выражение 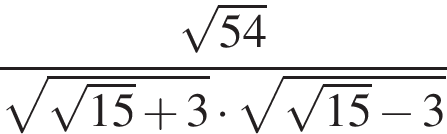 .
.
Решение. Имеем:
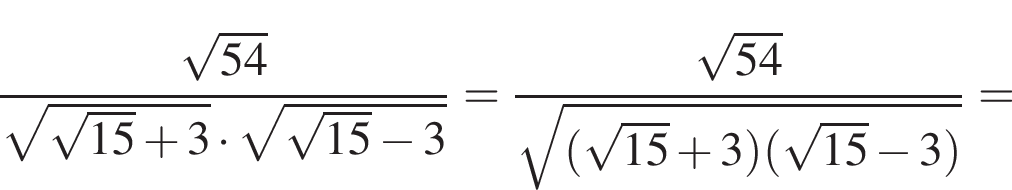
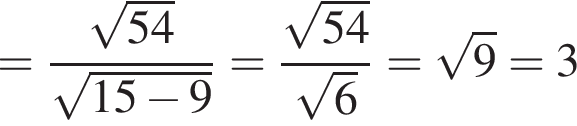 .
.
Ответ: 3.
21. Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 5 км/ч?
Решение. Пусть S км — расстояние, на которое от пристани отплыл рыболов. Зная, что скорость течения реки — 2 км/ч, а скорость лодки — 5 км/ч, найдём, что время, за которое он проплыл туда и обратно, составляет 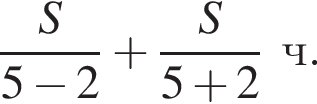 Учитывая, что он был на стоянке 2 часа и вернулся через 5 часов после отплытия можно составить уравнение:
Учитывая, что он был на стоянке 2 часа и вернулся через 5 часов после отплытия можно составить уравнение:
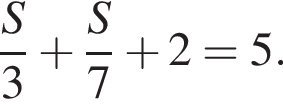
Отсюда S = 6,3 км.
Ответ: 6,3 км.
22. Постройте график функции 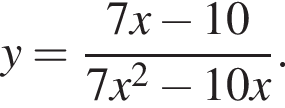 Определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
Определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.
Решение. Упростим выражение для функции:
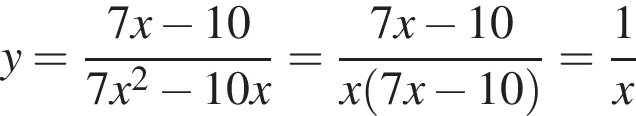 (при
(при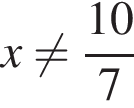 ).
).
Таким образом, получили, что график нашей функции сводится к графику функции 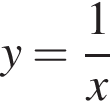 с выколотой точкой
с выколотой точкой 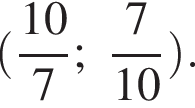
Построим график функции (см. рис.).
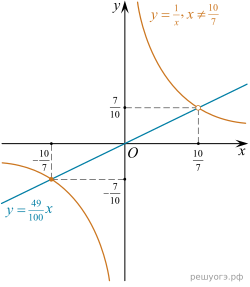
Заметим, что прямая  проходит через начало координат и будет иметь с графиком функции ровно одну общую точку только тогда, когда будет проходить через выколотую точку
проходит через начало координат и будет иметь с графиком функции ровно одну общую точку только тогда, когда будет проходить через выколотую точку 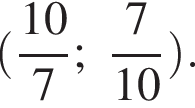 Подставим координаты этой точки в уравнение прямой и найдём коэффициент
Подставим координаты этой точки в уравнение прямой и найдём коэффициент 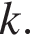
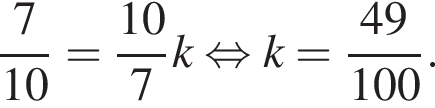
Ответ: 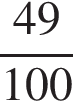 .
.
23. Прямая, параллельная основаниям AD и BC трапеции ABCD, проходит через точку пересечения диагоналей трапеции и пересекает ее боковые стороны AB и CD в точках E и  соответственно. Найдите длину отрезка EF, если
соответственно. Найдите длину отрезка EF, если 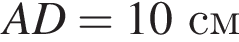 ,
, 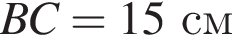 .
.
Решение.  1)
1)  по двум углам:
по двум углам:
a)  как вертикальные;
как вертикальные;
б)  как внутренние накрест лежащие углы при
как внутренние накрест лежащие углы при  и секущей BD.
и секущей BD.
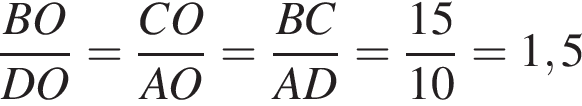
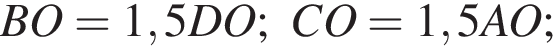
2)  по двум углам:
по двум углам:
а) 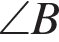 — общий;
— общий;
б)  как соответственные углы при
как соответственные углы при 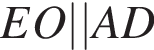 и секущей AB.
и секущей AB.
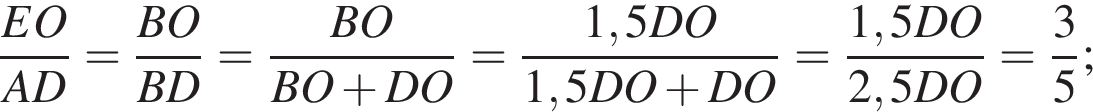
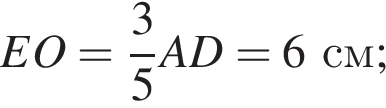
3) Аналогично, из подобия треугольников ACD и COF находим, что 
4) 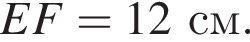
Ответ: 12 см.
24. Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
Решение. В задаче возможны два случая.
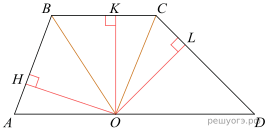 Первый случай, AD — одно из оснований. Проведём построения и введём обозначения как указано на рисунке. Рассмотрим треугольники OBH и BOK Рассмотрим треугольники OBH и OBK, они прямоугольные, углы HBO и KBO равны, OB — общая, следовательно, треугольники равны. Откуда OH = OK. Аналогично из треугольников KOC и COL получаем, что OK = OL. Таким образом, OH = OK = OL.
Первый случай, AD — одно из оснований. Проведём построения и введём обозначения как указано на рисунке. Рассмотрим треугольники OBH и BOK Рассмотрим треугольники OBH и OBK, они прямоугольные, углы HBO и KBO равны, OB — общая, следовательно, треугольники равны. Откуда OH = OK. Аналогично из треугольников KOC и COL получаем, что OK = OL. Таким образом, OH = OK = OL.
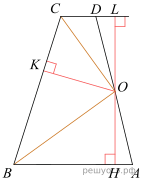 Второй случай, AD — одна из боковых сторон. Несмотря на другую геометрическую конфигурацию, доказательство полностью повторяет доказательство для первого случая.
Второй случай, AD — одна из боковых сторон. Несмотря на другую геометрическую конфигурацию, доказательство полностью повторяет доказательство для первого случая.
Приведем другое решение.
Точка О лежит на биссектрисе угла ABC, следовательно, она равноудалена от прямых AB и BC. Точка О лежит на биссектрисе угла , следовательно, она равноудалена от прямых BC и CD. Таким образом, точка О равноудалена от прямых AB, BC и CD.
25. Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.
Решение. 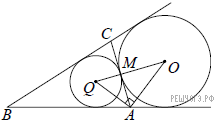 Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC. Точка касания M окружностей делит AC пополам. AQ и AO — биссектрисы смежных углов, значит, угол OAQ прямой. Из прямоугольного треугольника OAQ получаем: AM 2 = MQ · MO. Следовательно,
Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC. Точка касания M окружностей делит AC пополам. AQ и AO — биссектрисы смежных углов, значит, угол OAQ прямой. Из прямоугольного треугольника OAQ получаем: AM 2 = MQ · MO. Следовательно,
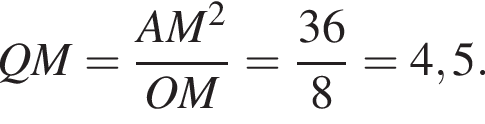
Ответ: 4,5.
| № задания | ответ |
| 1 | 57,6 |
| 2 | 9150 |
| 3 | 73 |
| 4 | 11461 |
| 5 | 9 |
| 6 | -4 |
| 7 | 2 |
| 8 | 110 |
| 9 | 02 |
| 10 | 0,5 |
| 11 | 134 |
| 12 | 9 |
| 13 | 1 |
| 14 | 8 |
| 15 | 51 |
| 16 | 14 |
| 17 | 2 |
| 18 | -1,5 |
| 19 | 3 |
| 20 | 3 |
| 21 | 6,3 |
| 22 | 
|
| 23 | 12 |
| 24 | - |
| 25 | 4,5 |












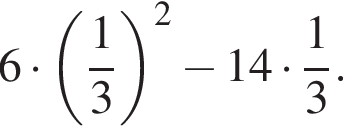
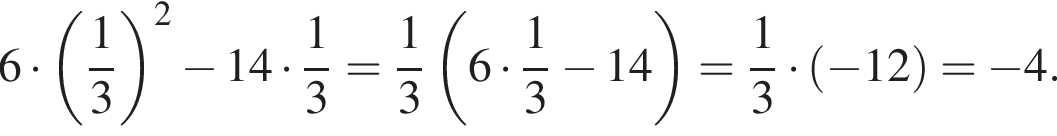
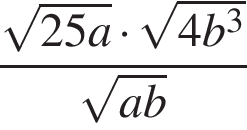 при a = 7 и b = 11.
при a = 7 и b = 11.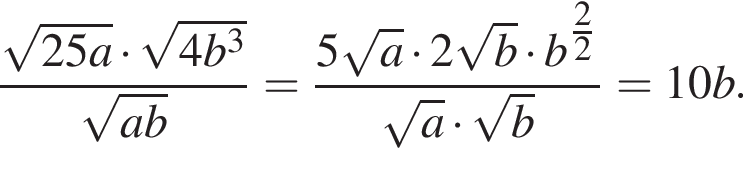
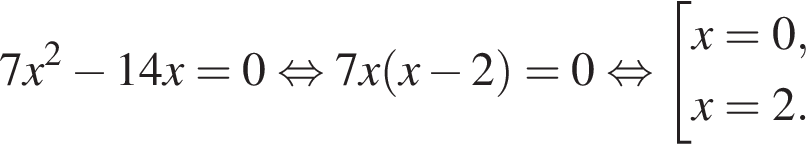
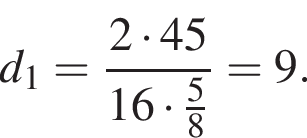
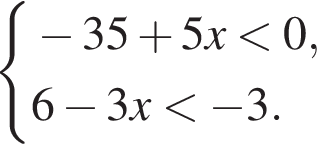
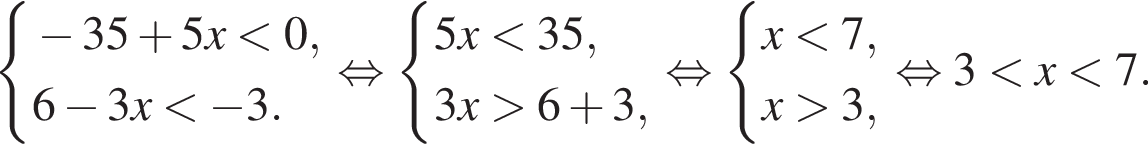
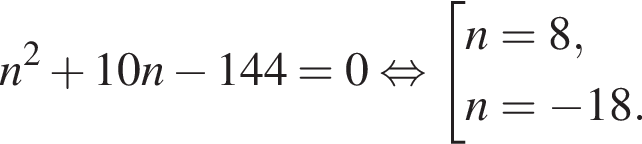

 Введём обозначение, как показано на рисунке. Углы 1 и 4 соответственные, поэтому ∠4 = ∠1 = 111°. Углы 2, 3 и 4 — это углы одного треугольника, сумма углов треугольника равна 180°, откуда ∠3 = 180° − 111° − 18° = 51°.
Введём обозначение, как показано на рисунке. Углы 1 и 4 соответственные, поэтому ∠4 = ∠1 = 111°. Углы 2, 3 и 4 — это углы одного треугольника, сумма углов треугольника равна 180°, откуда ∠3 = 180° − 111° − 18° = 51°. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 25. Найдите AC, если
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 25. Найдите AC, если 
 Проведём вторую высоту и введём обозначения, как показано на рисунке. Рассмотрим треугольники ABH и CKD, они прямоугольные, AB равно CD, BH равно CK, следовательно, эти треугольники равны, откуда
Проведём вторую высоту и введём обозначения, как показано на рисунке. Рассмотрим треугольники ABH и CKD, они прямоугольные, AB равно CD, BH равно CK, следовательно, эти треугольники равны, откуда 
 Углы
Углы 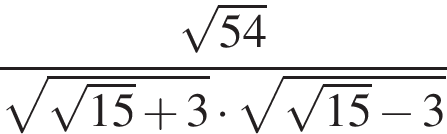 .
.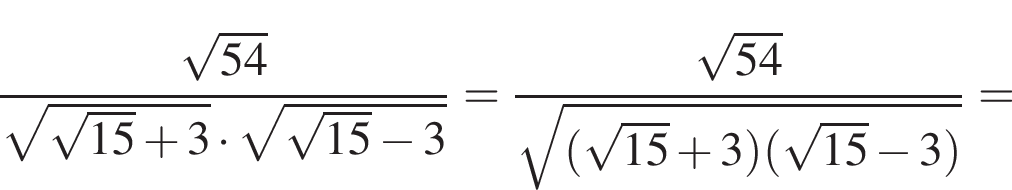
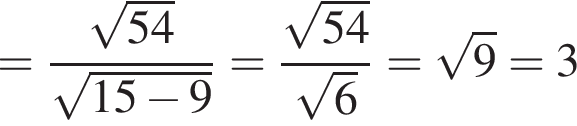 .
.
 1)
1)  Первый случай, AD — одно из оснований. Проведём построения и введём обозначения как указано на рисунке. Рассмотрим треугольники OBH и BOK Рассмотрим треугольники OBH и OBK, они прямоугольные, углы HBO и KBO равны, OB — общая, следовательно, треугольники равны. Откуда OH = OK. Аналогично из треугольников KOC и COL получаем, что OK = OL. Таким образом, OH = OK = OL.
Первый случай, AD — одно из оснований. Проведём построения и введём обозначения как указано на рисунке. Рассмотрим треугольники OBH и BOK Рассмотрим треугольники OBH и OBK, они прямоугольные, углы HBO и KBO равны, OB — общая, следовательно, треугольники равны. Откуда OH = OK. Аналогично из треугольников KOC и COL получаем, что OK = OL. Таким образом, OH = OK = OL. Второй случай, AD — одна из боковых сторон. Несмотря на другую геометрическую конфигурацию, доказательство полностью повторяет доказательство для первого случая.
Второй случай, AD — одна из боковых сторон. Несмотря на другую геометрическую конфигурацию, доказательство полностью повторяет доказательство для первого случая. Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC. Точка касания M окружностей делит AC пополам. AQ и AO — биссектрисы смежных углов, значит, угол OAQ прямой. Из прямоугольного треугольника OAQ получаем: AM 2 = MQ · MO. Следовательно,
Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC. Точка касания M окружностей делит AC пополам. AQ и AO — биссектрисы смежных углов, значит, угол OAQ прямой. Из прямоугольного треугольника OAQ получаем: AM 2 = MQ · MO. Следовательно,



















