Задание 11 ЕГЭ.
Смеси и сплавы.
В задачах на смеси и сплавы важно уметь определять концентрацию вещества.
Концентрация вещества в растворе (смеси, сплаве) – это отношение массы или объёма вещества к массе или объёму всего раствора (смеси, сплава).
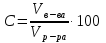
Как правило, концентрация выражается в процентах.
Что такое масса раствора, смеси, сплава?
Сейчас будет несколько очевидных мыслей. С точки зрения химии и физики – они не всегда выполняются, но для удобства и простоты, при составлении задач для ЕГЭ придерживаются именно этих предпосылок. Главное, чтобы вы не впали в ступор на экзамене, пытаясь понять, что же составители имели в виду.
Мысль 1.
| Масса раствора (смеси, сплава) равна сумме масс всех составляющих. |
Если мы смешаем 3 литра апельсинового сока и 7 литров воды, то получим 10 литров апельсинового нектара (сделаем предположение, что смешивание происходит в автоматическом режиме, а не вручную).
Мысль 2.
| При смешивании нескольких растворов (смесей, сплавов) масса нового раствора становится равной сумме всех смешанных растворов. |
Если мы смешаем 6 литров яблочного сока и 6 литров персикового сока – то получится 12 литров яблочно-персикового сока.
И ещё одна очевидность (последняя).
Мысль 3
| Масса растворённого вещества при смешивании двух растворов суммируется. |
Если мы смешаем 3 литра яблочного сока с 10% мякоти (0,3 л), и 5 литров яблочного сока с 5% мякоти (0,25 л), то получим 8 литров сока с 0,55 л мякоти (0,3+0,25).
Перейдём к задачам.
Задачи на смеси и сплавы.
Задачи на смеси и сплавы бывают двух основных видов:
Две смеси определённой массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
Строго говоря, подход к решению от этого не меняется. Во втором случае мы тоже смешиваем две смеси, просто в одной концентрация вещества больше 0, а в другой равна 0.
Пример 1.
В 5% раствор кислоты массой 3,8 кг добавили 1,2 кг чистой воды. Чему стала равна концентрация раствора (в процентах)?
Решение:
Для начала вычислим, сколько кислоты содержится в 5% растворе. Из 3,8 кг 5% - это кислота, а значит в растворе 0,05⋅3,8=0,19 кг кислоты.
Далее определим массу нового раствора. Как мы уже знаем – масса раствора равна массе его составляющих, т.е. 3,8 кг + 1,2 кг = 5 кг.
Поскольку в чистой воде кислоты нет, то в новом растворе количество кислоты не изменилось – 0,19 кг. Таким образом, концентрация кислоты стала равна  .
.
Ответ: 3,8.
Теперь попробуем решить задачу посложнее.
Пример 2.
Смешали 3 кг 5%-го водного раствора щелочи и 7 кг 15%-го водного раствора щелочи. Какова концентрация вновь полученного раствора? Ответ дайте в процентах.
Решение:
Давайте попробуем визуализировать ситуацию. 3 кг 5%-го водного раствора. Значит воды в этом растворе 95%.
Нарисуем: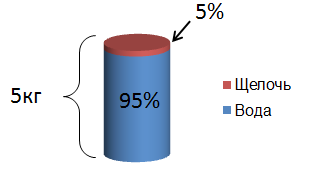
А теперь второй раствор:
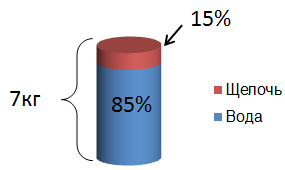
После смешивания, вновь получившийся раствор весит 3 кг + 7 кг = 10 кг. Обозначим количество щелочи в новом растворе за x, а количество воды – (10−x):
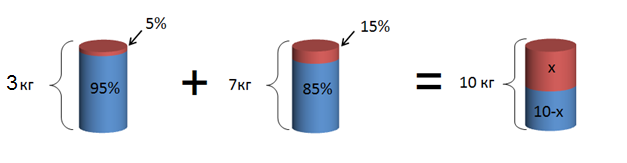 Теперь выразим количество щелочи в этих двух растворах в килограммах. В первом растворе – 0,05⋅3 = 0,15 кг щелочи и 3−0,15 = 2,85 кг воды, во втором 0,15⋅7 = 1,05 кг щелочи и 7−1,05 = 5,95 кг воды:
Теперь выразим количество щелочи в этих двух растворах в килограммах. В первом растворе – 0,05⋅3 = 0,15 кг щелочи и 3−0,15 = 2,85 кг воды, во втором 0,15⋅7 = 1,05 кг щелочи и 7−1,05 = 5,95 кг воды:
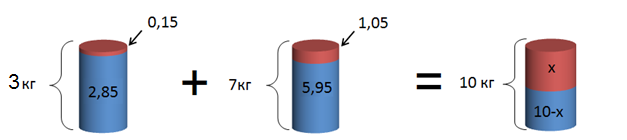
Из картинки видно, что количество щелочи в новом растворе равно сумме весов кислоты в старых растворах: x = 0,15+1,05 = 1,2 кг кислоты.
Теперь, зная количество щелочи в новом растворе и зная его массу, мы можем легко определить концентрацию:

Ответ: 12%
Визуализация приведена только для наглядности. На экзамене же можно кратко записать решение задачи:
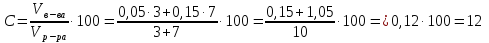
Такую же визуализацию удобно использовать в любых задачах на растворы, смеси и сплавы.
Пример 3.
Чернослив содержит 25% влаги. Его получают из сливы, содержащей 90% влаги, путём сушки. Сколько нужно килограммов сливы, для получения 5 кг чернослива?
Решение: Давайте попробуем нарисовать.
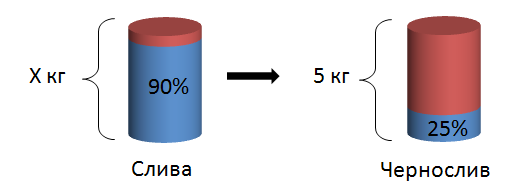
Количество сухого (красного на рисунке) вещества не изменилось. Изменилась лишь его пропорция. Найдём его вес. Поскольку сухого вещества в черносливе – 100% − 25% = 75%, то масса сухого вещества составит – 0,75⋅5 кг = 3,75 кг.
Нам нужно взять такое количество сливы, чтобы в нем было 3,75 кг сухого вещества. Обозначим вес необходимого количества сливы за x. По условию мы знаем, что сухого вещества в сливе - 100% − 90% = 10%, т.е. 0,1⋅x кг, а нам нужно 3,75 кг. Получается, что 0,1x = 3,75. Значит, х = 37,5. Для получения 5 кг чернослива, нам нужно взять 37,5 кг сливы.
Ответ: 37,5.
Или, используя формулу концентрации:  . Отсюда,
. Отсюда,
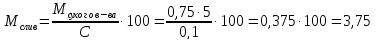
Пример 4.
Имеются два сплава серебра с медью. В первом содержится 10% серебра, во втором – 25%. Сколько килограммов второго сплава нужно добавить к 10 кг первого, чтобы получить сплав с 20% содержанием серебра?
Решение:
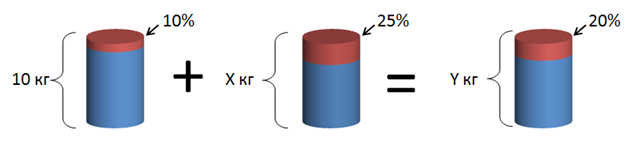
Обозначим за x искомый вес второго сплава, а за y – массу получившегося сплава.
Масса серебра в первом сплаве –10%⋅10 кг = 0,1⋅10 кг = 1 кг, во втором - 25%⋅ x = 0,25x, в новом сплаве – 20%⋅ y = 0,2y.
Теперь у нас есть система уравнений, решив которую найдём искомый x:

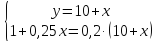

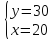
Получается, что добавив в 10 кг 10%-го сплава, 20 кг 25%-го сплава - мы получим 30 кг 20%-го сплава.
Ответ: 20.
Или, используя формулу концентрации: 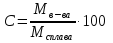 .
.
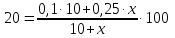
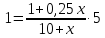
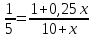
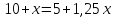


Подведём итоги.
Если вы заметили, во всех задачах мы сначала определяли, какое вещество влияет на концентрацию, назовём его «главным». А дальше следили за абсолютной величиной этого главного вещества (в килограммах, литрах). Если в раствор (сплав) что-то доливали, добавляли, то, в зависимости от состава «добавки», вес «главного» вещества либо изменялся, либо нет. Важно определить, что произошло с «главным» веществом, а дальше решение становится совсем простым.
А теперь попробуйте решить задачи самостоятельно.
Имеются два сплава с содержанием цинка 15% и 22%. Какова будет концентрация цинка, если сплавить 90 кг первого и 50 кг второго?
Сколько миллилитров 55%-го раствора уксуса нужно добавить к 500 мл 1%-го раствора, чтобы получить 5%-й раствор уксуса?
Смешали некоторое количество 12%-го раствора вещества с таким же количеством 22%-го раствора этого же вещества. Какова концентрация (в процентах) вещества в новом растворе?
В сосуд, содержащий 8 литров 14%-го раствора кислоты, добавили 12 литров воды. Сколько процентов кислоты содержится в новом растворе?
Сколько килограммов 17%-го сплава меди нужно добавить к 5 кг 10%-го сплава меди, чтобы получить 12%-й сплав?
В сосуд, содержащий 8 литров 35%-го водного раствора некоторого вещества, добавили 12 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Вишня содержит 89% влаги, а высушенная вишня – 12%. Сколько килограммов вишни требуется для получения 15 кг высушенной?
Имеется два сплава. Первый содержит 12% меди, второй – 21% меди. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 19,2% меди. На сколько килограммов масса первого сплава меньше массы второго?
Имеется два сосуда. Первый содержит 5 кг, а второй – 15 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 21% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Смешали некоторое количество 12%-го раствора уксуса с таким же количеством 6%-го раствора уксуса. Сколько процентов составляет концентрация уксуса в получившемся растворе?
Смешали некоторое количество 12%-го раствора уксуса с вчетверо большим количеством 9%-го раствора уксуса. Сколько процентов составляет концентрация уксуса в получившемся растворе?
Курага получается в процессе сушки абрикосов. Абрикосы содержат 84% воды, а курага – 20%. Сколько килограммов кураги получится из 45 кг абрикосов?
Свежие подосиновики содержат 78% воды, а сушёные – 12%. Сколько килограммов свежих подосиновиков требуется для получения 3 кг сушёных грибов?
Имеется два сплава. Первый содержит 20% олова, второй – 40% олова. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 36% олова. На сколько килограммов масса второго сплава больше массы первого сплава?
Имеется два раствора. Первый содержит 10% соли, второй – 20% соли. Из этих двух растворов получили третий раствор массой 50 кг, содержащий 12% соли. На сколько килограммов масса второго раствора меньше массы первого раствора?
Сколько килограммов воды нужно выпарить из 0,5 т целлюлозной массы, содержащей 85% воды, чтобы получить массу с содержанием 75% воды?
Морская вода содержит 5% соли по массе. Сколько процентов воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?
Кусок сплава меди и цинка массой 36 кг содержит 45% меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди?
Имеется кусок сплава меди с оловом общей массой 12 кг, содержащей 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы полученный новый сплав содержал 40% меди?
Сплав меди с серебром содержит серебра на 1845 г больше, чем меди. Если бы к нему добавить некоторое количество чистого серебра, по массе равное  массы чистого серебра, первоначально содержавшегося в сплаве, то получился бы новый сплав, содержащий 83,5% серебра. Какова масса сплава и каково первоначальное процентное содержание в нём серебра?
массы чистого серебра, первоначально содержавшегося в сплаве, то получился бы новый сплав, содержащий 83,5% серебра. Какова масса сплава и каково первоначальное процентное содержание в нём серебра?
Имеются два сплава золота и серебра. В одном сплаве количество этих металлов находятся в отношении 1:2, в другом – 2:3. Сколько граммов нужно взять от каждого сплава, чтобы получить 19 г сплава, в котором золото и серебро находятся в отношении 7:12?
Имеется лом стали двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла каждого из этих сортов, чтобы получить 140 т стали с 30%-ным содержанием никеля?
Имеются два сплава меди и цинка. В первом сплаве меди в 2 раза больше, чем цинка, а во втором меди в 5 раз меньше, чем цинка. Во сколько раз больше надо взять второго сплава, чем первого, чтобы получить новый сплав, в котором цинка было бы в 2 раза больше, чем меди?
Вычислите вес и процентное содержание серебра в сплаве с медью, зная, что сплавив его с 3 кг чистого серебра, получат сплав, содержащий 90% серебра, а, сплавив его с 2 кг сплава, содержащего 90% серебра, получат сплав, содержащий 84% серебра.
Два раствора, из которых первый содержит 0,8 кг, а второй 0,6 кг безводной серной кислоты, соединили вместе и получили 10 кг нового раствора серной кислоты. Вычислите вес первого и второго растворов в смеси, если известно, что безводной серной кислоты содержится в первом растворе на 10% больше.
В двух сплавах медь и цинк относятся как 5:2 и 3:4 (по весу). Сколько нужно взять килограммов первого сплава и сколько второго, чтобы после совместной переплавки получить 28 кг нового сплава с равным содержанием меди и цинка?
В двух сплавах медь и цинк относятся как 4:1 и 1:3. После совместной переплавки 10 кг первого сплава, 16 кг второго сплава и несколько килограммов чистой меди получили сплав, в котором медь и цинк относятся ка 3:2. Определить вес нового сплава.
Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй – 26% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Определите, сколько килограммов олова содержится в получившемся новом сплаве?
Имеются два сплава с различным процентным содержанием свинца. Вес одного 6 кг, вес другого 12 кг. От каждого из них отрезали по куску равного веса, после чего сплавили их с остатком другого куска. В результате процентное содержание свинца в обоих сплавах стало одинаковым. Сколько весил каждый отрезанный кусок?
От двух кусков сплава одинаковой массы, но с различным процентным содержанием меди, отрезали по куску равной массы. Каждый из отрезанных кусков сплавили с остатком другого куска, после чего процентное содержание меди в обоих кусках стало одинаковым. Во сколько раз отрезанный меньше целого?
Определить процент соли в растворе, если в 400 г раствора содержится 32 г соли.
Сколько сушёных груш получится из 50 кг свежих, если при сушке из свежих груш получается 15% сушёных?
Яблоко антоновка содержит 10,7% сахара. Сколько сахара содержится в 20 кг этих яблок?
Сколько сухой ромашки получится из 25 кг свежей, если она при сушке теряет 84% своей массы?
Мясо во время варения теряет 35% своего веса. Сколько следует взять сырого мяса, чтобы приготовить 130 порций варёного по 40 г в каждой порции?
Из 1 т медного колчедана, содержащего 2,5% меди, получено 22 кг меди. Сколько процентов меди удалось выделить и сколько процентов составили потери?
Сколько граммов йода содержится в 300 г его 6%-го раствора?
Сколько воды следует долить до 7,5 кг 12%-го раствора соли, чтобы получить 10%-ный раствор?
Сколько соли требуется добавить к 7,5 кг 12%-го раствора соли, чтобы получить 20%-ный раствор?
Имеется 735 г 16%-го раствора йода в спирте. Сколько граммов спирта следует долить к уже имеющемуся раствору, чтобы получить 10%-ный раствор?
К раствору, содержащему 40 г соли, добавили 200 г воды, после чего его концентрация уменьшилась на 10%. Сколько воды содержал раствор и какова была его концентрация?
До просушки влажность зерна была равна 23%, а после просушки оказалась равной 12%. На сколько процентов потеряло в весе зерно после просушки?
Ответы:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 17,5 | 40 | 17 | 5,6 | 2 | 14 | 120 | 120 |
|
|
|
|
|
|
|
|
|
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1,2 | 9 | 9,6 | 9 | 12 | 150 | 30 | 200 |
|
|
|
|
|
|
|
|
|
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 70 | 13,5 | 1,5 | 3165; 79,1 | 9; 10 | 40; 100 | 2 | 2,4; 80 |
|
|
|
|
|
|
|
|
|
| 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| 4; 6 | 7; 21 | 35 | 170 | 4 | 2 | 8 | 7,5 |
|
|
|
|
|
|
|
|
|
| 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 2,14 | 4 | 8 | 88; 12 | 18 | 1,5 | 0,75 | 441 |
|
|
|
|
|
|
|
|
|
| 41 | 42 |
|
|
|
|
|
|
| 160; 20 | 12,5 |
|
|
|
|
|
|
Решения:









Вишня содержит 89% влаги, значит, в ней 11% сухого вещества, в сушёной вишне 12% влаги, значит, в ней 88% сухого вещества. Тогда:







Значит, масса первого раствора 40 кг, а второго 200 – 40 = 160. Тогда масса первого раствора на 120 кг меньше массы второго.
Составим таблицы данных.
После смешивания растворов:
|
| Масса раствора, кг | % содержания вещества | Масса кислоты, кг |
| I раствор | 5 | x | 5∙0,01x |
| II раствор | 15 | y | 15∙0,01y |
| III раствор | 5+15 | 21 | 0,05x+0,15y или 0,21∙20 |
После смешивания равных масс этих растворов:
|
| Масса раствора, кг | % содержания вещества | Масса кислоты, кг |
| I раствор | т | x | т∙0,01x |
| II раствор | т | y | т∙0,01y |
| III раствор | 2т | 22 | 0,01т(x+y) или 0,22∙2т |
Составляем систему уравнений:


Значит, в первом растворе содержится 24% кислоты, а во втором – 20%. Тогда количество кислоты в первом растворе равно:  кг.
кг.
Абрикосы содержит 84% влаги, значит, в них 16% сухого вещества, в кураге 20% влаги, значит, в ней 80% сухого вещества. Тогда:




Подосиновик содержит 78% воды, значит, в нём 22% сухого вещества, в сушёном подосиновике 12% воды, значит, в нём 88% сухого вещества. Тогда:







Значит, масса первого сплава 50 кг, а второго 250 – 50 = 200. Тогда масса первого сплава на 150 кг меньше массы второго.



Значит, масса первого раствора 40 кг, а второго 50 – 40 = 10. Тогда масса второго раствора на 30 кг меньше массы первого.
В 500 кг целлюлозной массы содержится 85% воды, значит, в ней 15% целлюлозы, т.е.  кг. Нужно выпарить х кг воды из 500 кг целлюлозной массы так, чтобы в оставшихся
кг. Нужно выпарить х кг воды из 500 кг целлюлозной массы так, чтобы в оставшихся  кг содержалось 25% целлюлозы. Тогда:
кг содержалось 25% целлюлозы. Тогда:














Пусть масса серебра, содержащегося в сплаве, х кг, тогда масса меди по условию  г; масса сплава -
г; масса сплава -  г. Если к сплаву прибавить
г. Если к сплаву прибавить  г чистого серебра, то в новом сплаве массой г окажется серебра 83,5%. В новом сплаве серебра
г чистого серебра, то в новом сплаве массой г окажется серебра 83,5%. В новом сплаве серебра  и это, по условию, составляет 83,5% от , т.е.
и это, по условию, составляет 83,5% от , т.е.

Итак, в сплаве содержится 2505 г чистого серебра, значит, масса сплава 3165 г. Процентное содержание серебра в сплаве будет равно
Пусть от первого сплава взяли х г, тогда от второго сплава взяли  г. В первом сплаве золота
г. В первом сплаве золота  г, а во втором сплаве золота
г, а во втором сплаве золота  г. По условию в 19 г нового сплава золота
г. По условию в 19 г нового сплава золота  г. Итак,
г. Итак,

Значит, от первого сплава взяли 9 г, а от второго 19 – 9 = 10 г.
Пусть х т металла взяли из одного сорта, тогда  т взяли из другого сорта. Тогда
т взяли из другого сорта. Тогда


Значит, от одного сорта взяли 40 т, тогда от другого 140 – 40 = 100 т.
Пусть для получения нового сплава взяли х первого сплава и у второго сплава. В первом сплаве, по условию задачи, меди  ; во втором сплаве меди
; во втором сплаве меди  . Новый сплав, имеющий массу
. Новый сплав, имеющий массу  , содержит меди
, содержит меди  . Значит,
. Значит,

Значит, второго сплава надо взять в 2 раза больше, чем первого.
Пусть вес сплава х кг, а процентное содержание серебра в этом сплаве у%. Тогда

Значит, вес сплава 3 кг, а процентное содержание серебра в этом сплаве 80%. Тогда,  кг серебра в этом сплаве.
кг серебра в этом сплаве.
Пусть х кг вес первого раствора, тогда (10 – х) кг – вес второго раствора; у% – процентное содержание серной кислоты в первом растворе, тогда (у – 10)% – во втором растворе. По условию, 0,01ху = 0,8 кг, а 0,01(10 – х)(у – 10) = 0,6 кг. Решим систему уравнений:

Значит, вес первого раствора в смеси 4 кг, тогда вес второго 10 – 4 = 6 кг.
Пусть х кг – вес первого раствора, тогда вес второго раствора – (28 – х) кг. По условию известно, что меди в первом растворе содержится  кг, во втором -
кг, во втором -  кг, а в третьем -
кг, а в третьем -  кг. Тогда:
кг. Тогда:


Значит, первого раствора нужно взять 7 кг, а второго 28 – 7 = 21 кг.
В этой задаче мы составили уравнение по меди, но можно составить уравнение и по цинку.
В первом сплаве меди  кг, цинка
кг, цинка  кг. Во втором сплаве меди
кг. Во втором сплаве меди  кг, а цинка
кг, а цинка  кг. Обозначим через х вес чистой меди, тогда вес третьего сплава равен (10 + 16 + х) = (26 + х) кг. В третьем сплаве меди
кг. Обозначим через х вес чистой меди, тогда вес третьего сплава равен (10 + 16 + х) = (26 + х) кг. В третьем сплаве меди  кг, а цинка
кг, а цинка  кг. Уравнение составляем либо по меди, либо по цинку:
кг. Уравнение составляем либо по меди, либо по цинку:



Значит, вес чистой меди 9 кг, тогда вес третьего сплава 26 + 9 = 35 кг.
Пусть х% - содержание цинка в первом и во втором сплаве. Тогда меди в первом сплаве  , а олова во втором сплаве
, а олова во втором сплаве  . Зная, что новый сплав содержит 30% цинка, составляем уравнение:
. Зная, что новый сплав содержит 30% цинка, составляем уравнение:

Значит, цинка в первом и во втором сплаве по 30%, меди в первом сплаве 30%, олова во втором сплаве 44%. Тогда олова в первом сплаве  кг, во втором сплаве
кг, во втором сплаве  кг, и в третьем сплаве
кг, и в третьем сплаве  кг.
кг.
Обозначим х% - содержание свинца в первом сплаве, у% - содержание свинца во втором сплаве, т кг – отрезанные куски от первого и от второго сплава, тогда  кг осталось от первого сплава,
кг осталось от первого сплава,  кг – осталось от второго сплава. По условию известно, что после сплавки остатка первого сплава с отрезанным куском от второго; и остатка второго сплава с отрезанным куском от первого, содержание свинца в получившихся сплавах стало одинаковым. Составляем уравнение:
кг – осталось от второго сплава. По условию известно, что после сплавки остатка первого сплава с отрезанным куском от второго; и остатка второго сплава с отрезанным куском от первого, содержание свинца в получившихся сплавах стало одинаковым. Составляем уравнение:


Значит, и от первого и от второго куска отрезали 4 кг.
Пусть имеются два сплава массой х кг с различным содержанием меди. Пусть в первом сплаве меди  %, во втором сплаве меди
%, во втором сплаве меди  %. От каждого сплава массой х кг отрезали одинаковые куски массой у кг. Далее,
%. От каждого сплава массой х кг отрезали одинаковые куски массой у кг. Далее,  кг первого сплава сплавили с у кг второго сплава, а
кг первого сплава сплавили с у кг второго сплава, а  кг второго сплава сплавили с у кг первого сплава. В результате оба новых сплава имеют одинаковое процентное содержание меди. В
кг второго сплава сплавили с у кг первого сплава. В результате оба новых сплава имеют одинаковое процентное содержание меди. В  кг первого сплава меди
кг первого сплава меди  ; в у кг второго сплава
; в у кг второго сплава  меди. Значит, в первом новом сплаве массой х кг меди будет . Значит, процентное содержание меди в этом сплаве будет . Аналогично, в
меди. Значит, в первом новом сплаве массой х кг меди будет . Значит, процентное содержание меди в этом сплаве будет . Аналогично, в  кг второго сплава и в у кг первого сплава меди будет . Процентное содержание меди в этом сплаве будет . По условию, процентное содержание меди в обоих кусках одинаково. Составляем уравнение:
кг второго сплава и в у кг первого сплава меди будет . Процентное содержание меди в этом сплаве будет . По условию, процентное содержание меди в обоих кусках одинаково. Составляем уравнение:

Так как по условию  , то
, то 

Значит, отрезанный кусок меньше целого в 2 раза.




Пусть х кг необходимое количество свежего мяса,  количество варёного мяса. Тогда
количество варёного мяса. Тогда  , значит,
, значит,  .
.
Из 1 т = 1000 кг медного колчедана с содержанием меди 2,5% должно получиться  кг меди. По условию задачи получено 22 кг меди, значит,
кг меди. По условию задачи получено 22 кг меди, значит,  удалось выделить, тогда потери составляют 12%.
удалось выделить, тогда потери составляют 12%.












Пусть х г первоначальный вес раствора, тогда концентрация соли в нём была  . Когда прибавили к этому раствору 200 г, концентрация соли в нём стала
. Когда прибавили к этому раствору 200 г, концентрация соли в нём стала  . По условию, концентрация соли уменьшилась на 10%, значит,
. По условию, концентрация соли уменьшилась на 10%, значит, 




Значит, первоначальный вес раствора 200 г, тогда воды в нём содержалось 160г, концентрация раствора была  .
.
Пусть х - масса зерна до сушки, в нём воды 0,23х, следовательно, сухого зерна х - 0,23х = 0,77х. После сушки масса зерна стала у, воды в нём 0,12у, сухого зерна у - 0,12у = 0,88у. Приравняем количества сухого зерна до и после сушки





Значит, потери составляют  , в процентах это 12,5%
, в процентах это 12,5%
10







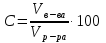
 .
. 

 Теперь выразим количество щелочи в этих двух растворах в килограммах. В первом растворе – 0,05⋅3 = 0,15 кг щелочи и 3−0,15 = 2,85 кг воды, во втором 0,15⋅7 = 1,05 кг щелочи и 7−1,05 = 5,95 кг воды:
Теперь выразим количество щелочи в этих двух растворах в килограммах. В первом растворе – 0,05⋅3 = 0,15 кг щелочи и 3−0,15 = 2,85 кг воды, во втором 0,15⋅7 = 1,05 кг щелочи и 7−1,05 = 5,95 кг воды:

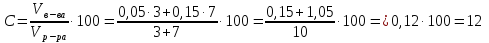

 . Отсюда,
. Отсюда,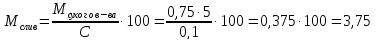


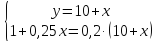

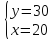
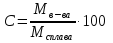 .
. 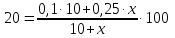
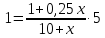
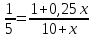
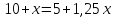


 массы чистого серебра, первоначально содержавшегося в сплаве, то получился бы новый сплав, содержащий 83,5% серебра. Какова масса сплава и каково первоначальное процентное содержание в нём серебра?
массы чистого серебра, первоначально содержавшегося в сплаве, то получился бы новый сплав, содержащий 83,5% серебра. Какова масса сплава и каково первоначальное процентное содержание в нём серебра?