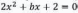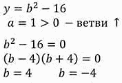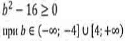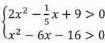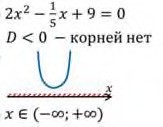Алгебра, 9 класс
Тема. Решение неравенств второй степени с одной переменной.
Цель урока: познакомить учащихся с алгоритмом решения неравенств на основе свойств квадратичной функции, сформировать умения решать неравенства данного вида.
ПЯТНАДЦАТОЕ ДЕКАБРЯ
Сегодня на уроке мы будем воспитывать ответственность, дисциплинированность, аккуратность.
Ход урока
1. Организационный момент.
«С тех пор как существует мирозданье,
Такого нет, кто б не нуждался в знанье.
Какой мы ни возьмем язык и век,
Всегда стремится к знанью человек »
2. Актуализация.

4. Новый материал.
Ребята. Предлагаю вам посмотреть видеоурок по теме http://www.youtube.com/watch?v=1JT30bpfCPs
Изучаем вместе
Определение:
Неравенства вида:
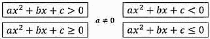
где х - переменная, a, b, c - некоторые числа и а≠0 называются неравенствами второй степени с одной переменной.
В левой части этих неравенств записан квадратный трёхчлен.
Решение этих неравенств можно рассматривать как нахождение промежутков, в которых функция у = ax² +bx+c принимает положительное или отрицательное значение
Решение этих неравенств сводится к нахождению множества значений переменной х, при которых квадратный трёхчлен принимает положительные или отрицательные значения.
Для этого достаточно проанализировать, как расположен график функции у = ax² +bx+c в координатной плоскости:
Куда направлены ветви параболы – вверх или вниз.
Пересекает ли парабола ось x и если пересекает, то в каких точках.
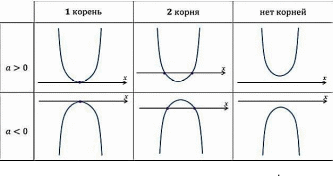
АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА
ax² +bx+c 0 и ax² +bx+c
Определить направление ветвей параболы: при а 0 ветви направлены вверх; при а ветви направлены вниз.
2. Найти дискриминант квадратного трехчлена ax² + bx+c=0 и выяснить имеет ли трехчлен корни.
3. Если трехчлен имеет корни, то отмечаем их на оси Х и через отмеченные точки схематически проводим параболу с учетом направления ее ветвей.
4. Если трехчлен не имеет корней, то схематически изображаем параболу, расположенную в верхней полуплоскости при а 0 или в нижней полуплоскости при а .
5. Находим на оси Х промежутки, для которых точки параболы расположены выше оси Х, если решаем неравенство ax² +bx+c 0 или ниже оси Х, если решаем неравенство ax² +bx+c
7. Записать ответ.
Рассмотрим примеры.
Задание №1.
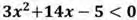
Рассмотрим квадратичную функцию:
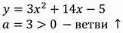
Графиком этой функции является парабола, ветви которой направлены вверх.
Выясним, как расположена эта парабола относительно оси Х.
Для этого решим уравнение:
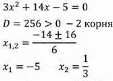
Это уравнение имеет корни 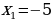 и
и 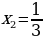 , значит, парабола пересекает ось х в двух точках, абсциссы которых равны
, значит, парабола пересекает ось х в двух точках, абсциссы которых равны 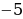 и
и 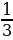 .
.
Покажем схематически, как расположена парабола в координатной плоскости. Отметим эти значения на оси Х:
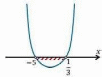
Из рисунка видно, что функция принимает отрицательное значение когда x принадлежит промежутку от – 5 до 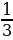 .
.
Следовательно, множеством решения неравенства 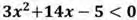 является промежуток (–5;
является промежуток (–5; 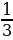 ).
).
Ответ: х ∈ (–5; 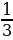 ).
).
Заметим, что в рассмотренном способе нас не интересовала вершина параболы, всего лишь нужно было знать, куда направлены ветви параболы и каковы абсциссы точек ее пересечения с осью Х.
Рассмотрим второе неравенство.
Задание №2.
Решить неравенство: 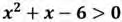
Рассмотрим квадратичную функцию:
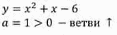
Имеем параболу ветви которой направлены вверх.
Для нахождения точек пересечения с осью Х решим уравнение: 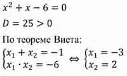
Уравнение имеет корни 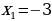 и
и 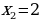 , значит, парабола пересекает ось х в двух точках, абсциссы которых равны
, значит, парабола пересекает ось х в двух точках, абсциссы которых равны 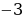 и
и 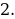
Покажем схематически, как расположена парабола в координатной плоскости. Отметим эти значения на оси Х:
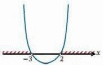
Из рисунка видно, что функция принимает положительные значения, если x принадлежит промежутку х ∈ (–∞; –3) и х ∈ (2; + ∞).
Следовательно, решением неравенства является объединение промежутков.
Ответ: х ∈ (–∞; –3) ∪ (2; + ∞)
Задание №3.
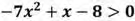
Рассмотрим функцию:
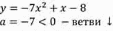
Ее графиком является парабола, ветви которой направлены вниз определим, как расположен график относительно оси Х.
Для этого решим ур авнение:
авнение:
Так как дискриминант равен Д= –223, то есть он меньше нуля, это означает что это уравнение корней не имеет.
Значит, парабола не имеет общих точек с осью Х.
Показав схематически расположение параболы в координатной плоскости, найдем, что функция не принимает положительное значение ни при каких значениях x.
Ответ: решением данного неравенства является пустое множество ∅.
Задание №4.
Определить, при каком значении переменной b уравнение имеет корни:
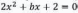
Найдем дискриминант этого уравнения:

Тогда выполнение задания сводиться к решению неравенства второй степени. Причём с нестрогим знаком, больше либо равно.
Применив алгоритм, найдем корни уравнения:
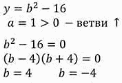
Изобразим их на числовой прямой:
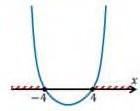
Уравнение имеет корни:
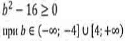
Задание №5.
Решить систему неравенств:
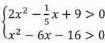
Решим каждое неравенство в отдельности. В первом случае:
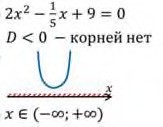
Во втором случае:
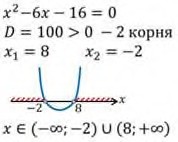
Мы получили решение двух неравенств второй степени. Вернёмся к системе. Решением системы будет пересечение двух решений. Значит, решением системы будет объединение промежутков:
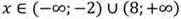
Домашнее задание.
Выучить п. 14. Посмотреть видео по теме урока Решить № 305(б), 307(б).







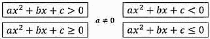

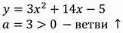
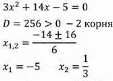
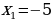 и
и 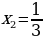 , значит, парабола пересекает ось х в двух точках, абсциссы которых равны
, значит, парабола пересекает ось х в двух точках, абсциссы которых равны 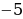 и
и 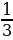 .
.
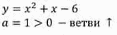
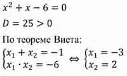
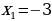 и
и 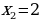 , значит, парабола пересекает ось х в двух точках, абсциссы которых равны
, значит, парабола пересекает ось х в двух точках, абсциссы которых равны 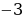 и
и 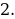

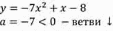
 авнение:
авнение: