Муниципальное бюджетное общеобразовательное учреждение
Нижневерейская средняя школа
городского округа г. Выкса Нижегородской области
Решение систем линейных уравнений методом Крамера
Физико-математическое отделение
Секция математическая
Работу выполнил(а):
Ученик(ца) 9 класса
Саргсян Роза Никогаёсовна
Научный руководитель:
Учитель МБОУ Нижневерейской
средней школы
Максимова Валентина Владимировна
2020 г.
Содержание
| Введение | 3 |
| Обзор литературы | 5 |
Системы линейных уравнений | 5 |
Основные определения и обозначения | 6 |
Решение систем линейных уравнений методом Крамера | 7 |
Немного из истории | 7 |
Описание метода Крамера | 9 |
Решение системы двух линейных уравнений | 11 |
Решение системы трех линейных уравнений | 14 |
Проведение обучающего эксперимента | 19 |
Заключение | 24 |
| Список литературы | 25 |
Введение
Системы уравнений встречаются в древних текстах II тысячелетия до н. э. Системы уравнений применяли для решения задач в Вавилоне и Египте. Уже тогда люди умели составлять своеобразные системы уравнений и решать их. Многие системы становились громоздкими, и их запись в общем виде была трудной к восприятию. Решение этой проблемы предложил в 1675 г. немецкий математик Г.В. Лейбниц (1646 – 1716) – он ввёл нижние индексы при буквах. Ещё Г.В. Лейбниц в 1693 году обратил внимание на то, что при изучении систем линейных уравнений наиболее существенной является таблица, состоящая из коэффициентов, и показал, как из этих коэффициентов (в случае m=n) строить так называемые определители, при помощи которых исследуются системы линейных уравнений.
Г. Крамером в 1750 году было установлено правило, применимое к любой системе n линейных уравнений c n неизвестными. Оно носит название правило Крамера. Построение полной теории произвольных систем линейных уравнений было закончено только спустя 100 лет Л. Кронекером.
Применение правила Крамера при практическом решении большого числа линейных уравнений может встретить различные трудности, так как нахождение определителей высокого порядка связано с весьма большими вычислениями. Поэтому были разработаны методы приближённого решения систем линейных уравнений, наиболее известным из которых является метод Гаусса.
Система линейных уравнений может иметь как одно единственное решение (определённая система), так и несколько и даже бесконечное множество решений (неопределённая система); может также оказаться, что система линейных уравнений не имеет ни одного решения (несовместная система).
Способы решения систем линейных уравнений – очень интересная и важная тема. Системы уравнений и методы их решения рассматриваются в школьном курсе математики начиная с 7 класса, но недостаточно широко. Многие математические модели построены на основе ситуаций из реальной жизни, одной из таких моделей являются системы уравнений. Системы уравнений – это инструмент для решения многих задач из смежных дисциплин, связанных с математикой. Для того, чтобы перейти к исследованию данной темы, также нужно было познакомиться с темой матриц и определителей. Этот же материал вообще в школьной программе не изучается.
Актуальность темы «Решение систем линейных уравнений методом Крамера» заключается в следующем: применение этого метода способствует развитию логической культуры, значительно облегчает работу при решении систем уравнений с большим количеством неизвестных и еще, задачи по теме «Системы уравнений» включены в основной государственный экзамен: задание 9 и задание 21 (раздел «Алгебраические выражения, уравнения, неравенства и их системы») и умение решать их несколькими способами значительно увеличивает шанс справиться с заданием.
Цель моей работы заключается в том, чтобы изучить метод Крамера для решения систем линейных уравнений для дальнейшего применения на практике. Для достижения любой цели необходимо выполнить какие-то определенные задачи. Мне нужно выполнить следующие задачи: исследовать литературу по данной теме; научиться решать системы линейных уравнений методом Крамера; отобрать и классифицировать материал по теме, а также провести практическую часть работы: разработать и провести занятия с одноклассниками по знакомству с методом Крамера и определить уровень освоения данной темы.
Для решения задач были использованы следующие методы исследования: анализ методической литературы (поиск информации из разных источников); практическая работа; обработка полученных данных (составление обобщающих таблиц, диаграмм); работа в компьютерных программах Microsoft Word, Excel, Microsoft PowerPoint.
Гипотеза: С помощью данного метода увеличивается скорость решения систем линейных уравнений.
Объект исследования: Метод Крамера.
Предмет исследования: Системы линейных уравнений.
Обзор литературы.
Выполнение научно-практической работы позволило мне более подробно изучить метод Крамера для решения систем линейных уравнений.
В работе, мною был реализован метод Крамера для решения системы линейных уравнений. Было использовано необходимое условие существования решения, т.е. не равенство нулю главного определителя системы. Отличительная черта этого метода заключается в неоднократном вычислении определителя матрицы. С вычислительной точки зрения это трудоемкая операция с ростом количества элементов. В работе были рассмотрены системы 3-го и 2-го порядков, а определители вычислялись непосредственно. Системы 2-го порядка взяты из учебника алгебры 7 класса автора А.Г. Мерзляка. Системы 3-го порядка взяты из учебника для студентов «Введение в алгебру» автор А.И. Кострикин.
При исследовании решений системы линейных уравнений методом Крамера использовались учебники Л.Я. Куликова «Алгебра и теория чисел.» – М.: Высшая школа, 1979 и «Сборник задач по алгебре и теории чисел» – М.: Просвещение, 1993, скачанные в формате pdf.
Системы линейных уравнений
Линейные уравнения вида а х = b и системы линейных уравнений вида

(1)
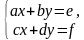
с действительными коэффициентами a, b, c, d, e, f изучаются в средней школе. Наша цель – научиться оперировать с системой линейных уравнений самого общего вида:

(2)

Здесь m и n – произвольные целые положительные числа.
Основные определения и обозначения.
Следует обратить внимание на весьма экономное и удобное обозначение коэффициентов системы (2): коэффициент 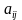 стоит в i-м уравнении при j-й неизвестной
стоит в i-м уравнении при j-й неизвестной 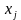 . Число
. Число  называется свободным членом i-го уравнения. Система (2) называется однородной, если
называется свободным членом i-го уравнения. Система (2) называется однородной, если  = 0 для i=1, 2, . . ., m. При любых
= 0 для i=1, 2, . . ., m. При любых  линейную систему
линейную систему

(2´)
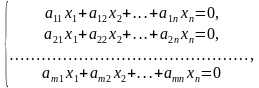
называют однородной системой, или ещё – приведенной системой для системы (2).
Коэффициенты при неизвестных составляют прямоугольную

(3)
таблицу

,
называемую матрицей размера m×n (m×n-матрицей или квадратной матрицей порядка n при m=n) и сокращенно обозначаемую символом буквой А.
Наряду с матрицей (3) рассматривают еще расширенную матрицу (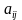 |
| ) системы (2), получаемую из (3) добавлением столбца
) системы (2), получаемую из (3) добавлением столбца 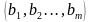 свободных членов; для ясности он отделен от остальных столбцов вертикальной чертой.
свободных членов; для ясности он отделен от остальных столбцов вертикальной чертой.
Если каждое из уравнений системы (2) обращается в тождество после замены неизвестных 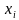 числами
числами 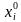 , то набор из n чисел
, то набор из n чисел 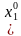 ,
,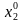 ,…,
,…, ) называется решением системы (2). Говорят также, что набор
) называется решением системы (2). Говорят также, что набор 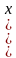 ,
,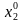 ,…,
,…, ) удовлетворяет всем уравнениям системы (2). Система уравнений называется совместной, если она имеет хотя бы одно решение, определенной, если имеет ровно одно решение, и неопределенной, если имеет более одного решения. Система уравнений, не имеющая ни одного решения, называется несовместной.
) удовлетворяет всем уравнениям системы (2). Система уравнений называется совместной, если она имеет хотя бы одно решение, определенной, если имеет ровно одно решение, и неопределенной, если имеет более одного решения. Система уравнений, не имеющая ни одного решения, называется несовместной.
Исследовать систему уравнений – значит выяснить, совместна она или нет, и если совместна, то – определенна или нет. Решить систему – значит найти все ее решения.
Решение систем линейных уравнений методом Крамера
2.1. Немного из истории.

Швейцарский математик. Педагог. Один из создателей линейной алгебры.
Габриэль Крамер родился 31 июля 1704 года в городе Женева, Швейцария. Мальчик вырос в семье врача. Уже в детстве опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики. В восемнадцать лет успешно защитил диссертацию.
В 1724 году Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Юноша так понравился магистрату, что специально для него и еще одного кандидата на место преподавателя учреждена отдельная кафедра математики.
Ученый много путешествовал по Европе, перенимая опыт у знаменитых математиков своего времени: Иоганна Бернулли и Леонарда Эйлера в Базеле, Эдмунда Галлея в Лондоне. Со многими из них продолжал переписываться всю жизнь.
После путешествия Крамер возобновил преподавательскую работу в Женевском университете в 1729 году. В это время участвовал в конкурсе Парижской Академии и занял второе место.
Талантливый ученый написал множество статей на самые разные темы: геометрия, история, математика, философия. В 1730 году опубликовал труд по небесной механике. В 1740-е годы Иоганн Бернулли поручил Крамеру подготовить к печати сборник своих работ. Это задание Габриэль выполнил в 1742 году, опубликовав его сборник в 4-х томах.
Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является «Введение в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Габриэль выстроил систему линейных уравнений и решил ее с помощью алгоритма, названного позже его именем: метод Крамера.
Габриэль Крамер скончался 4 января 1752 года в французском городе Баньоле-сюр-Сезе.
2.2. Описание метода Крамера.
Метод Крамера (правило Крамера) основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может.
Для системы n линейных уравнений с n неизвестными
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
Алгоритм решения систем линейных уравнений методом Крамера.
Найти главный определитель системы:
.
Найти вспомогательные определители (их число совпадает с числом неизвестных)  определитель
определитель  получаем из определителя ∆ заменой j-го столбца на столбец свободных членов .
получаем из определителя ∆ заменой j-го столбца на столбец свободных членов .


Три случая при решении систем линейных уравнений.
1) Если главный определитель не равен нулю, то система имеет единственное решение:  .
.
Система совместна и определенна.
2) Если главный определитель равен нулю, а хотя бы один из определителей  , то система решений не имеет.
, то система решений не имеет.
Система несовместна.
3) Если главный определитель равен нулю и все вспомогательные определители тоже равны нулю, то система имеет бесконечно много решений.
С истема совместна и неопределенна.
Решение системы двух линейных уравнений методом Крамера.
Для начала рассмотрим систему двух линейных уравнений с двумя переменными:
Решением данной системы будет пара чисел, при подстановке которых вместо  оба уравнения обращаются в верные равенства.
оба уравнения обращаются в верные равенства.
Составим таблицу (матрицу А) из коэффициентов при неизвестных данной системы уравнений и таблицу свободных членов В:
Мы имеем квадратную матрицу А второго порядка. Диагональ, идущая из левого верхнего угла матрицы в правый нижний, называется ее главной диагональю, другая диагональ называется побочной. Если из произведения элементов, стоящих на главной диагонали вычесть произведение элементов побочной диагонали, то мы получим значение определителя матрицы А.
 .
.
При замене первого столбца столбцом свободных членов, получаем вспомогательный определитель
При замене второго столбца столбцом свободных членов, получаем
Далее по формулам Крамера мы находим неизвестные переменные. Таким образом, 
Найти значения  и
и  возможно только при условии, если
возможно только при условии, если  .
.
Рассмотрим решение системы уравнений с двумя переменными методом Крамера.
Пример 1. Р Решить систему линейных уравнений методом Крамера.
Следовательно, система является определенной. Для нахождения ее решения вычисляем вспомогательные определители.
Так как главный определитель не равен нулю, то система имеет единственное решение.

Ответ: (2; 5)
Пример 2. Решить систему линейных уравнений методом Крамера.
Так как  ,
,  0, а
0, а  0, следовательно, система не имеет решений.
0, следовательно, система не имеет решений.
Ответ: решений нет.
Пример 3. Решить систему линейных уравнений методом Крамера.
Так как  и
и  ,
, , то система имеет бесконечно много решений.
, то система имеет бесконечно много решений.
Ответ: ∞
Решение системы трех линейных уравнений методом Крамера.
Перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель:
Определителем матрицы третьего порядка называется число, определяемое равенством:
 .
.
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.
Рис.1.1. Рис.1.2.
Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из рисунка (1.1.), а последующие три слагаемые берутся со знаком минус и определяются из рисунка (1.2).
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, , .
И, наконец, ответ рассчитывается по формулам:
 .
.
Рассмотрим решение системы уравнений с тремя переменными методом Крамера.
Пример 4. Решить систему линейных уравнений методом Крамера
Следовательно, система является определенной. Для нахождения ее решения вычисляем вспомогательные определители.
Так как главный определитель не равен нулю, то система имеет единственное решение.


Ответ: (2; 1; -1)
Пример 5. Решить систему линейных уравнений методом Крамера
Так как  ,
,  0,
0,  , а
, а  0, то система не имеет решений.
0, то система не имеет решений.
Ответ: решений нет.
Пример 6. Решить систему линейных уравнений методом Крамера
Находим определители:
Для проверки определителей можно воспользоваться любым онлайн-калькулятором, решающим методом Крамера.
Так как главный определитель не равен нулю, то система имеет единственное решение.
Итак, х1 = -152, х2 = 270, х3 = -254.
Ответ: (-152; 270; -254)
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю. Таков следующий пример.
Пример 7. Решить систему линейных уравнений методом Крамера
Находим определители:
Следовательно, система является определенной. Для нахождения ее решения вычисляем вспомогательные определители.
,
Так как главный определитель не равен нулю, то система имеет единственное решение.
.
Ответ: (2; -1; 1).
Проведение обучающего эксперимента.
Теперь, когда мне стал понятен принцип решения систем линейных уравнений методом Крамера, я решила проверить, насколько данный метод понятен моим одноклассникам, и можно ли его изучать в средней школе. Для начала я объяснила им новый способ решения системы линейных уравнений. А затем провела небольшую самостоятельную работу, в которой первую систему нужно было решить тремя способами (методом подстановки, сложения и Крамера), вторую систему одноклассники могли решить любым удобным способом.
Итак, ход I занятия (20 минут).
Знакомство с новым способом решения системы линейных уравнений.
Пример решения системы уравнений


Ответ:(3;1)
Домашнее задние. Решить систему уравнений тремя способами:
Метод подстановки.







Ответ:
Метод алгебраического сложения.





Ответ:
Метод Крамера.
Ответ: 
Ход II занятия (20 минут).
Самостоятельная работа.
Решить систему уравнений методами сложения, подстановки и
методом Крамера:
Решить систему уравнений любым способом:


Ответ:(1,2; -0,7)
В эксперименте приняли участие 13 человек. Подстановкой правильно решили первую систему уравнений 6 человек, сложением -11 человек, методом Крамера - 9 человек. Для решения второй системы способ мог быть выбран любой. Из 10 человек, выбравших метод Крамера, 7 человек решили систему правильно.
Результаты работ были занесены в таблицу и по ней для большей наглядности составлены диаграммы.
| № п/п | Ф.И обучающихся | 1 система уравнений | 2 система уравнений |
| подстановкой | сложением | Методом Крамера | подстановкой | сложением | Методом Крамера. |
| 1 | Быков Дм. | - | + | + |
|
| +/+ |
| 2 | Вялов С. | - | + | + |
|
| +/ - |
| 3 | Горячкина Ан. | - | + | + |
|
| +/+ |
| 4 | Дыбо Ал. | + | - | - | +/- |
|
|
| 5 | Иванова О. | + | + | + |
|
| +/ + |
| 6 | Кузнецов Р. | - | + | - |
| +/- |
|
| 7 | Кузовников А. | + | - | - |
|
| +/ - |
| 8 | Романов П. | - | + | - |
|
| +/ + |
| 9 | Самодуров Вл. | + | + | + |
| +/+ |
|
| 10 | Саргсян Р. | + | + | + |
|
| +/+ |
| 11 | Симакина Д. | + | + | + |
|
| +/ + |
| 12 | Фесенко Н. | - | + | + |
|
| + / - |
| 13 | Филатов И. | - | + | + |
|
| +/ + |
|
|
| 46% | 85% | 69% | 7,5% | 15,5% | 77% / 54% |
Вывод: Мои одноклассники овладели методом Крамера для решения систем линейных уравнений не хуже, чем методами подстановки и сложения. Более того, если есть возможность выбора способа решения, то 77% обучающихся остановились на новом методе.
Заключение.
Метод Крамера в представленной мною работе более подробно рассматривается для решения систем двух линейных уравнений с двумя неизвестными и систем трех линейных уравнений с тремя неизвестными. В основе этого метода лежат элементарные преобразования над коэффициентами системы, записанными в определители матрицы.
В результате выполнения работы:
Изучена литература по методам решения систем линейных уравнений.
Подобраны и решены системы линейных уравнений методом Крамера.
Проведены занятия с одноклассниками по изучению нового метода решения систем линейных уравнений.
Метод Крамера ускоряет процесс решения некоторых систем линейных уравнений и позволяет существенно сократить время на нахождение решений системы двух линейных уравнений. Его можно изучать на уроках алгебры. Метод Крамера доступен для изучения обучающимися 7-9 классов при решении систем двух линейных уравнений с двумя неизвестными и может быть предложен ученикам, как дополнительный метод решения систем уравнений.
Список литературы
Алгебра: 7 класс: учебник для учащихся общеобразовательных организаций/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – 2е изд., дораб. – М.: Вентана-Граф, 2017.
Википедия – свободная энциклопедия http://ru.wikipedia.org
РИА «Руспех» https://ruspekh.ru/people/gabriel-kramer
Куликов Л.Я. Алгебра и теория чисел. – М.: Высшая школа, 1979.
Куликов Л.Я., Макаленко А.И., Фомин А.А. Сборник задач по алгебре и теории чисел: Учебное пособие для студентов физико-математических специальностей пединститутов. – М.: Просвещение, 1993.
А.И. Кострикин Введение в алгебру.: Учеб. для студ. ун-та, обучающихся по специальности «Математика» и «Прикладная математика»: В 2 ч. – М.: Физ.-мат. лит.,2000. – Ч. 1. Основы алгебры.
Методические указания по изучению темы «Системы линейных уравнений». – Горький: ГГПИ им. Горького, 1988.
РЕЦЕНЗИЯ
на исследовательскую работу: Решение систем линейных уравнений методом Крамера.
Автор работы: обучающаяся 9 класса, 15 лет
Работа представлена на 25 страницах основного текста. Структура работы соответствует требованиям конкурса.
Работа носит исследовательский характер и посвящена изучению решения систем линейных уравнений методом Крамера. Цель и задачи соответствуют заданным исследованиям. В пункте 1 рассмотрены основные определения систем уравнений и их обозначения. Во втором пункте подробно описан метод Крамера для систем 2го и 3го порядков. Автор успешно владеет методикой так называемых определителей в решении систем линейных уравнений, опираясь на справочную литературу, которую описывает во 2 пункте. Работа иллюстрирована диаграммами опроса обучающихся.
Результаты, представленные в работе, имеют практическую значимость. Автор излагает материал полно и доступно согласно структуре работы. Результаты исследования были обсуждены с одноклассниками, которые получили рекомендации от автора.
Работа представляет интерес и в целом соответствует требованиям, предъявляемым для участия в научно – практической конференции обучающихся городского округа город Выкса. Рецензент выражает автору благодарность за проделанную работу и желает дальнейших научных успехов.
Рецензент работы: учитель математики В.В. Максимова
25








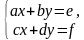

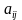 стоит в i-м уравнении при j-й неизвестной
стоит в i-м уравнении при j-й неизвестной 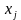 . Число
. Число  называется свободным членом i-го уравнения. Система (2) называется однородной, если
называется свободным членом i-го уравнения. Система (2) называется однородной, если 
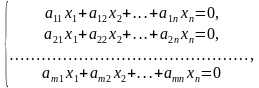
 ,
, 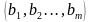 свободных членов; для ясности он отделен от остальных столбцов вертикальной чертой.
свободных членов; для ясности он отделен от остальных столбцов вертикальной чертой.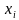 числами
числами 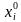 , то набор из n чисел
, то набор из n чисел 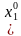 ,
,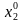 ,…,
,…, ) называется решением системы (2). Говорят также, что набор
) называется решением системы (2). Говорят также, что набор 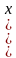 ,
,


















