17.03., 19.03. та 31.03.2020 р. 8 клас. Геометрія. Площа паралелограма

Площа паралелограма

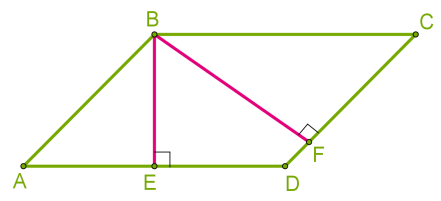
Необхідно визначити, що таке висота паралелограма.

Це перпендикуляр, проведений з будь-якої точки сторони паралелограма до прямої, що містить протилежну паралельну сторону. Зазвичай, висоту проводять з вершини паралелограма. Оскільки паралелограм має дві пари паралельні сторони, тоді він має висоти двох різних довжин.

Висота BE, проведена між довгими сторонами, коротше висоти BF, проведеної між короткими сторонами.

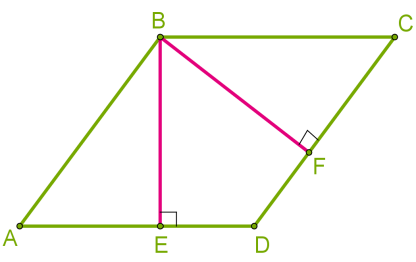
Оскільки сторони ромба однакові, тоді висоти ромба також однакові BE=BF.

Площа довільного паралелограма

Площа паралелограма дорівнює добутку висоти і сторони, до якої проведена висота.

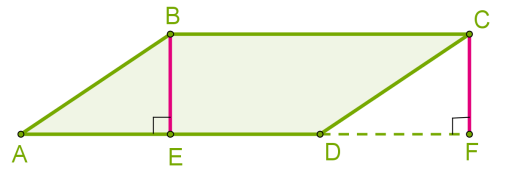
Проведемо висоти з двох вершин B і C до сторони AD.

Прямокутні трикутники ABE і DCF рівні (рівні гіпотенузи, як протилежні сторони паралелограма і рівні катети, як відстань між паралельними прямими).

Паралелограм ABCD і прямокутник EBCF — рівновеликі, оскільки складаються з рівних фігур:

S_ABCD = S_ABE+S_EBCD, SEBCF = S_EBCD + S_DCF.

Отже, площа паралелограма визначається так само, як площа прямокутника:

S_EBCF = BE⋅BC, S_ABCD=BE⋅BC=BC⋅AD.

Якщо позначити сторону через a, висоту через h, тоді: S_п−гр=a⋅h

Для визначення площі паралелограма можна використовувати коротку сторону і висоту, проведену до короткої сторони.

Розв'яжи. 1.

Дано: CD= 5 см, AD= 9 см, BF=5 см. Знайти: S(ABCD).

Відповідь: площа паралелограма ABCD дорівнює _____см²

2. Сторони паралелограма дорівнюють 3 см і 5 см, а висота, проведена до більшої сторони, дорівнює 4,1 см.Обчисли висоту, проведену до меншої сторони.

Відповідь: висота, проведена до меншої сторони - см.

Додаткове питання:

чи залежить величина площі фігури від того, за якою формулою площі вона обчислюється?

• Так
• Ні
• Іноді

Домашнє завдання. 17.03.2020 р. Опрацювати п. 21.

Домашнє завдання. 19.03.2020 р. Повторити п. 21. Виконати вправи № 698, № 703.

Домашнє завдання. 31.03.2020 р. Повторити п. 21. Виконати вправи №707, № 710.