30.04.2020 р. 8 клас. Геометрія. Повторення. Теорема Фалеса. 05.05.2020 р. Подібні трикутники

Два трикутники називаються подібними, якщо їхні відповідні кути рівні, а відповідні сторони пропорційні.

Маємо трикутники ABC і DEF.

Якщо відомо, що AB/DE = BC/EF = AC/DF = k і ∠A = ∠D; ∠B = ∠E; ∠C = ∠F, можна зробити висновок, що ΔABC∼ΔDEF.

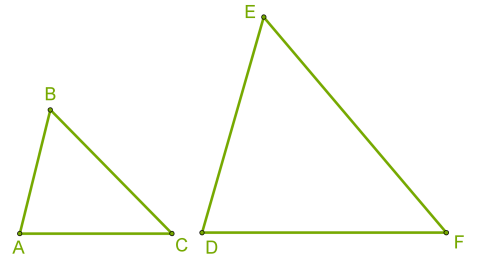
Під час запису подібності трикутників важливо дотримуватися порядку букв. Рівним кутам відповідають певні букви.

Число k, яке дорівнює співвідношенню відповідних сторін трикутників, називається коефіцієнтом подібності трикутників.

Щоб визначити, чи є трикутники подібними, необов'язково знати довжини всіх сторін і градусні міри всіх кутів трикутників. Це можна зробити простіше, використовуючи ознаки подібності трикутників.

Перша ознака подібності трикутників: за двома кутами. Якщо два кути одного трикутника дорівнюють двом кутам другого трикутника, то такі трикутники подібні.

Друга ознака подібності трикутників: за двома сторонами та кутом між ними. Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника та кути, утворені цими сторонами, рівні, то такі трикутники подібні.

Третя ознака подібності трикутників: за трьома сторонами. Якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники подібні.

Співвідношення периметрів двох подібних трикутників дорівнює коефіцієнту подібності трикутників:

P_ABC/P_DEF = k.

Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки й на іншій його стороні.

Теорема Фалеса. Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки й на другій його стороні.

Теорема про пропорційні відрізки. Якщо паралельні прямі перетинають сторони кута, то відрізки, що утворилися на одній стороні кута, пропорційні відповідним відрізкам, що утворилися на другій стороні кута.

Теорему Фалеса використовують, щоб поділити відрізок на декілька рівних частин.

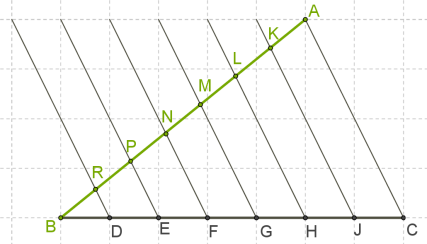
Необхідно поділити відрізок AB на 7 рівних частин. Намалюємо кут, на одній стороні якого лежить відрізок AB. Сторону кута BC намалюємо по клітинках і використаємо клітинки для поділу сторони на 7 рівних частин:

BD = DE = EF = FG = GH = HJ = JC. Кінці обох відрізків з'єднаємо, отримаємо AC.

Проведемо прямі, паралельні AC, що починаються в точках J, H, G, F, E, D отримаємо 7 паралельних прямих (знову використовуємо клітинки).

Якщо BD = DE = EF = FG = GH = HJ = JC і AC ∥ JK ∥ HL ∥ GM ∥FN ∥ EP ∥ DR, то за теоремою Фалеса, BR = RP = PN = NM = ML = LK = KA.

30.04.2020 р. Скласти конспект пункту 11. Виконати вправу № 392.

05.05.2020 р. Скласти конспект матеріалу. Пункти 12, 13, 14. Виконати вправу № 833.