

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 02.08.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 14.07.2025 06:33
Яско Оксана Валентиновна
учитель математики и информатики
43 года
Местоположение
Беларусь, Могилев
Специализация
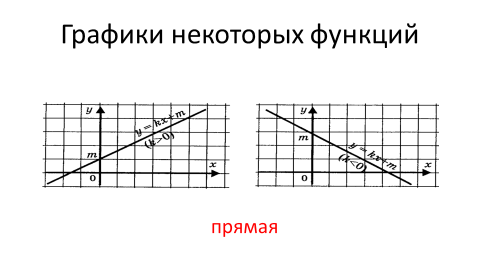
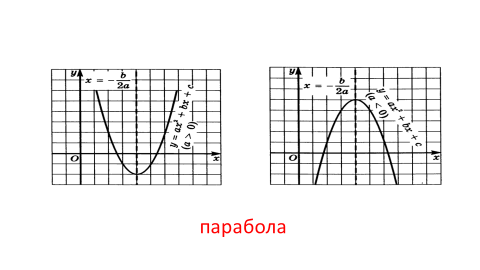
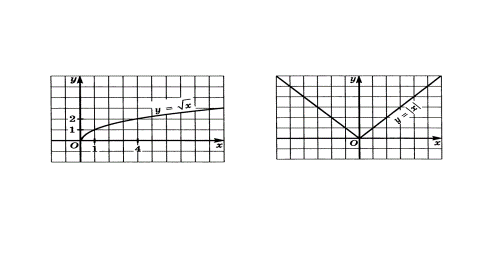
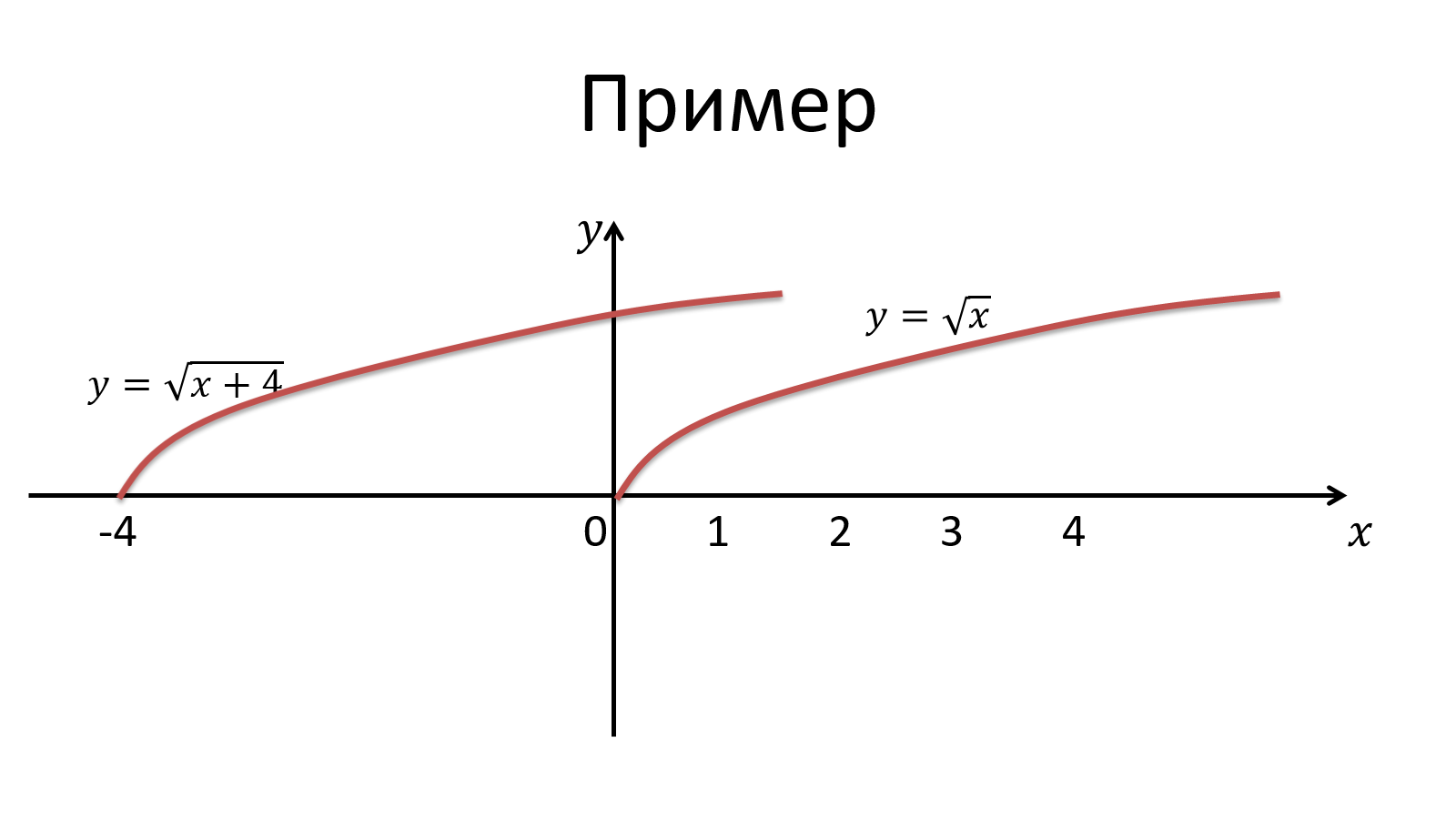
01. Числовые функции. Определение и способы задания
Категория:
Математика
10.06.2016 16:10



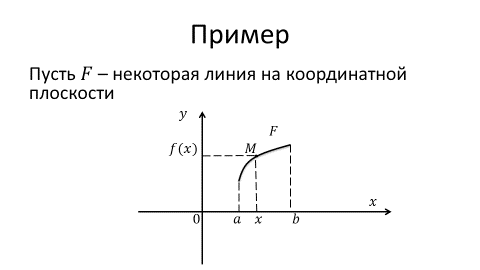










Геометрия 7 класс
Электронная тетрадь по алгебре 8 класс...
Алгебра 11 класc
Электронная тетрадь по алгебре 10 класс...
Алгебра 8 класс ФГОС
Математика и игры в средней школе
Алгебра 10 класс ФГОС
Геометрия 9 класс ФГОС
© 2016, Яско Оксана Валентиновна 1999 34
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы