10 класс. Параллелепипед.

КОУ ВО «ЦЛПДО»

Разработка уроков-консультаций по геометрии в 10 классе "Свойства прямоугольного параллелепипеда".

Подготовила Л.И.Гоптарь.

-Воронеж-

2020 г.

Цели урока:

1. Проверить уровень усвоения теоретических знаний по свойствам прямоугольного параллелепипеда.

2. Формировать у обучающихся навык применения изученных свойств при решении задач.

3. Развивать у учащихся пространственное мышление, самостоятельность.

4. Воспитывать коммуникативные умения и навыки, адекватную самооценку.

Формы работы на уроке:

фронтальный опрос;

индивидуальная самостоятельная работа.

Дидактические материалы:

листы для самоконтроля;

карточки с заданиями;

карточка с самостоятельной работой.

Учебник. Геометрия: учебник для 10-11 классов средней школы, авторы: Л. С. Атанасян, В. Ф, Бутузов, С. Б. Кадомцев.

Ход урока.

1. Организационный момент.

Сообщение темы и цели урока.

Изложение плана урока.

2. Разминка (блиц-опрос).

-Сформулируйте определение прямоугольного параллелепипеда.

-Сформулируйте свойства прямоугольного параллелепипеда.

-Сколько двугранных углов имеет параллелепипед?

-Какой прямоугольный параллелепипед называется кубом?

-Как найти длину диагонали прямоугольного параллелепипеда?

-Как найти сумму длин всех его ребер?

-Как найти полную поверхность прямоугольного параллелепипеда?

3. Работа в тетрадях:

 Учимся на чужих ошибках.

Приложение 1 (рисунок №3, №4).

Решаем задачи №1, 2 с объяснением, дополнительно устные задачи №3, 4.

Задача №5. Ученик собирает макет и отвечает на поставленный вопрос, все в тетрадях выполняют чертеж и записывают вывод.

4. Работа в парах.

Приложение 1 (карточки №5-№9).

5. Физкультминутка:

Кабинет, в котором мы занимаемся имеет форму параллелепипеда. Покажите боковые грани, основания, диагонали.

6. Самостоятельная работа.

Дополнительная задача. Из сборника ЕГЭ 3000 задач, под редакцией А. Л. Семенова, И. В. Ященко. №5

7. Подведение итогов. Оценки.

8. Дополнительное задание:  № 192, 194, глава 2, параграф 22-24.

Приложение 2.

Вставить пропущенные символы, знаки, закончить предложение, чтобы получилось верное утверждение.

Задание№6 .

Дана пирамида SABCD,

ABCD - квадрат, SA ┴ (ABC)

1. SD … CD

2. SB … BC

3. (SAD) … (ABC)

4. (SAB) … (ABC)

5. ∆SAD … ∆SAB

6. ∆SBC … ∆SDC

Задание№7 .

Дан тетраэдр SABC, ABC – прямоугольный треугольник (⁰), SA=SB=SC… гипотенузы AB - основание высоты тетраэдра (точка О).

Точка О является ... около треугольника ABC.

3. Проекциями боковых ребер на плоскость основания являются отрезки …

4. Плоскости ASB и ABC …

5. Треугольники SAO, SBO, SCO …

Задание№8 .

Основанием прямоугольного параллелепипеда является квадрат со стороной, равной 5 см. Расстояние от бокового ребра до скрещивающейся с ним диагонали параллелепипеда равно …

Задание№9 .

Три измерения прямоугольного параллелепипеда равны 1 см, 2 см, 3 см.

Сумма длин всех ребер равна …

Сумма площадей всех его граней равна …

Длины его диагоналей равны …

Задание№10 .

ABCDA₁ B₁C₁D₁ - прямоугольный параллелепипед.

Треугольник AB₁D …

... угол между диагональю B₁D и плоскостью основания.

Содержимое разработки.

OC 4 двугранных угла 10 двугранных углов AC II α AB ┴ α , CD ┴ α , B €, D € α, AB=CD AO ┴ α, AC и AB – наклонные, AC=AB Тетраэдр имеет –

Параллелепипед имеет –

BO=OC 6 12 " width="640"

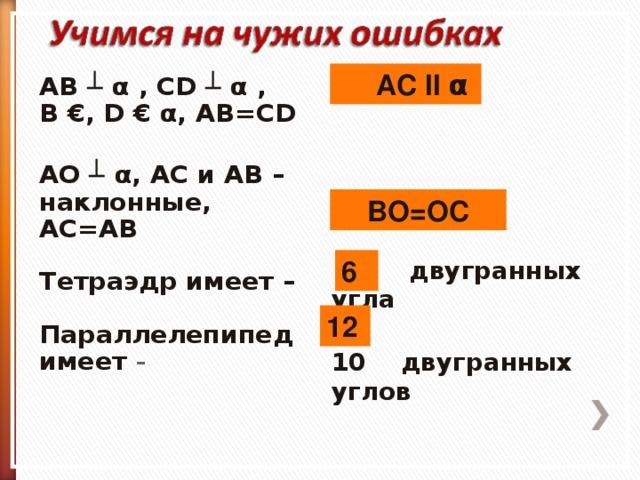
AC ∩ α

BOOC

4 двугранных угла

10 двугранных углов

AC II α

AB ┴ α , CD ┴ α , B €, D € α, AB=CD

AO ┴ α, AC и AB – наклонные, AC=AB

Тетраэдр имеет –

Параллелепипед имеет –

BO=OC

6

12

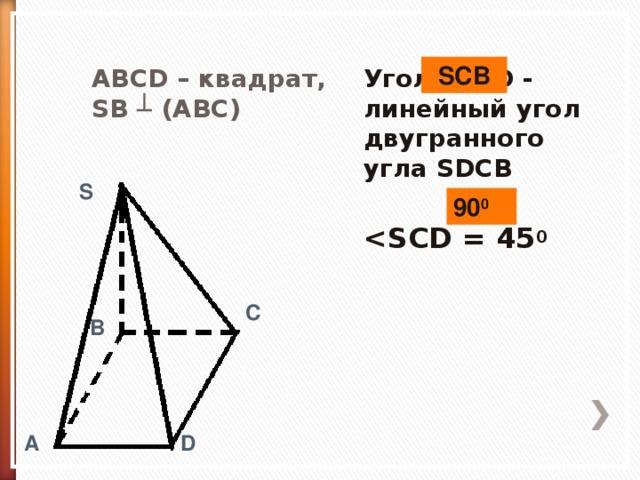
SCB

ABCD – квадрат, SB ┴ (ABC)

Угол SCD - линейный угол двугранного угла SDCB

0

S

90 0

C

B

A

D

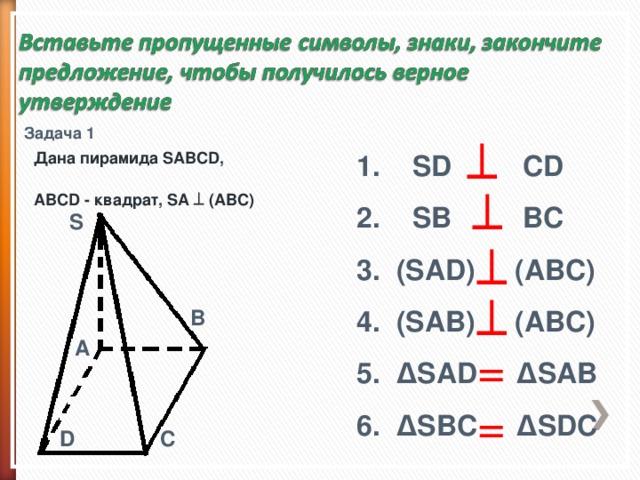
Задача 1

┴

Дана пирамида SABCD,

ABCD - квадрат, SA ┴ (ABC)

• SD CD

• SB BC

• (SAD) (ABC)

• (SAB) (ABC)

• ∆ SAD ∆SAB

• ∆ SBC ∆SDC

┴

S

┴

┴

B

A

=

=

C

D

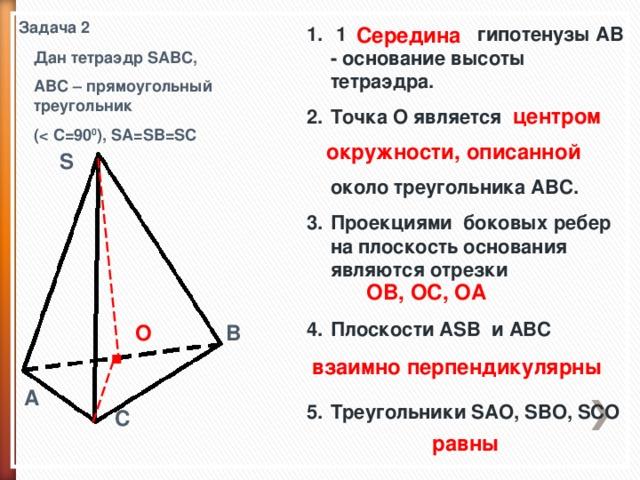
Задача 2

Середина

• 1 . гипотенузы AB - основание высоты тетраэдра.

• Точка О является около треугольника ABC.

• Проекциями боковых ребер на плоскость основания являются отрезки

• Плоскости ASB и ABC

• Треугольники SAO, SBO, SCO

Дан тетраэдр SABC,

ABC – прямоугольный треугольник

( C=90 0 ), SA=SB=SC

центром

окружности, описанной

S

OB, OC, OA

.

B

O

взаимно перпендикулярны

A

C

равны

Задача 3

Основанием прямоугольного параллелепипеда является квадрат со стороной, равной 5 см. Расстояние от бокового ребра до скрещивающейся с ним диагонали параллелепипеда равно

C 1

B 1

5 √2 /2 см

О

D 1

A 1

C

B

D

A

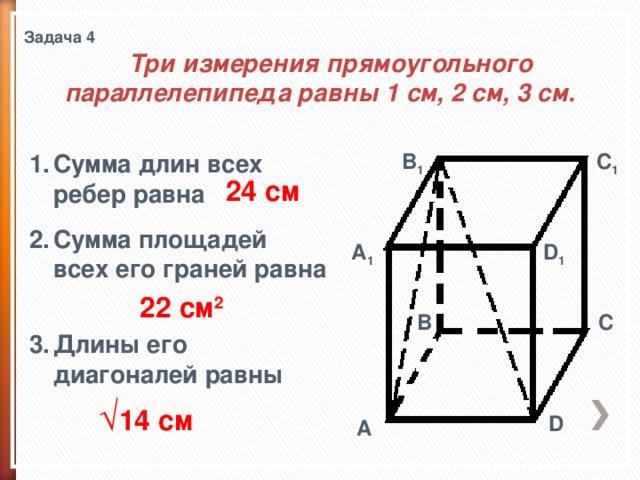
Задача 4

Три измерения прямоугольного параллелепипеда равны 1 см, 2 см, 3 см.

B 1

C 1

• Сумма длин всех ребер равна

• Сумма площадей всех его граней равна

• Длины его диагоналей равны

24 см

A 1

D 1

22 см 2

B

C

√ 14 см

D

A

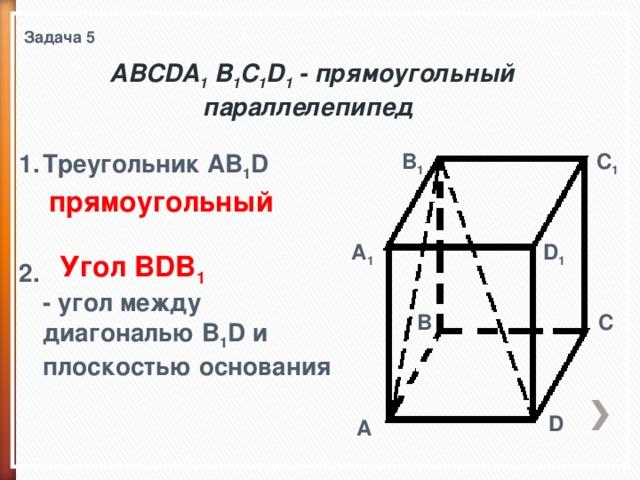
Задача 5

ABCDA 1 B 1 C 1 D 1 - прямоугольный параллелепипед

• Треугольник AB 1 D

C 1

B 1

2. - угол между диагональю B 1 D и плоскостью основания

прямоугольный

A 1

D 1

Угол BDB 1

C

B

D

A

Вариант 1

Вариант 2

В прямоугольном параллелепипеде измерения равны 6 см, 8 см, 10 см.

Найдите диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания

В прямоугольном параллелепипеде измерения равны 5 см, 7 см, √ 47 см.

Найдите диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания

Спасибо за урок.