11-класс.Геометрия.Конустун аянты.

Бишкек шаары. №66 «Ден соолуктун жана

өнүгүүнүн мектеби» гимназия-окуу тарбия комплекси

9-класс ГЕОМЕТРИЯ

Тема: ⸹63.4 Конустун аянты

И.Б.Бекбоев, А.А Бөрүбаев, А.А.Айылчиев.

Математика мугалими:

Маликова Д.Н.

Бугунку сабакта:

• Конустун, кесилген конустун каптал жана толук беттеринин аянттарын табуунун формулалары менен таанышасыңар;
• Маселелерди чыгарууга көнүгөсүңөр.
• Биздин жашообузда геометриядан алган билим, көндүмдөрдү колдонууга үйрөнөсүңөр.

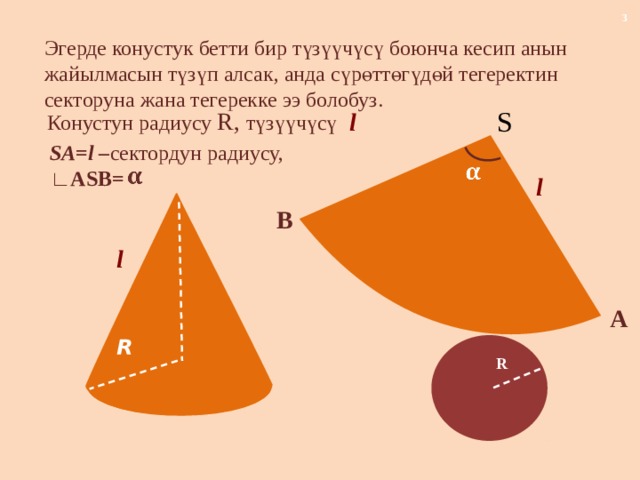
Эгерде конустук бетти бир түзүүчүсү боюнча кесип анын жайылмасын түзүп алсак, анда сүрөттөгүдөй тегеректин секторуна жана тегерекке ээ болобуз.

S

Конустун радиусу R, түзүүчүсү

l

SA=l – сектордун радиусу, ∟ASB=

l

B

l

A

R

R

Конустун каптал бетинин аянты сектордун аянтына барабар

болот.

r – тегеректин радиусу, α – жаанын чоңдугу, R – конустун негизинин радиусу, l – конустун түзүүчүсү

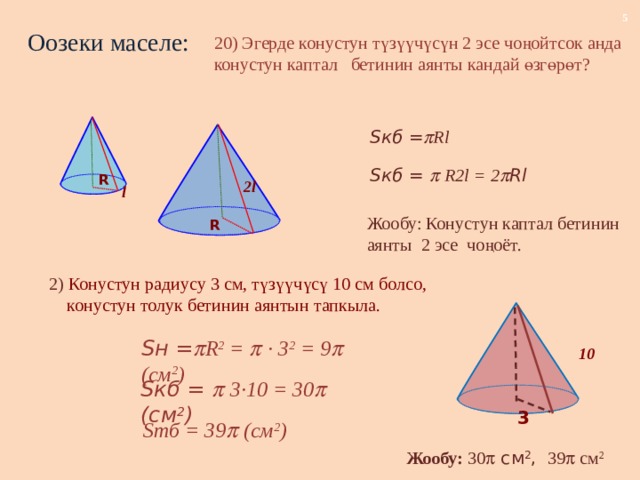
Оозеки маселе:

20) Эгерде конустун түзүүчүсүн 2 эсе чоңойтсок анда конустун каптал бетинин аянты кандай өзгөрөт?

Sкб =  Rl

Sкб =  R2l = 2  Rl

R

2l

l

Жообу: Конустун каптал бетинин аянты 2 эсе чоңоёт.

R

2) Конустун радиусу 3 см, түзүүчүсү 10 см болсо,

конустун толук бетинин аянтын тапкыла.

Sн =  R 2 =  · 3 2 = 9  (см 2 )

10

Sкб =  3·10 = 30  (см 2 )

3

Sтб = 39  (см 2 )

Жообу: 30  см 2 , 39  см 2

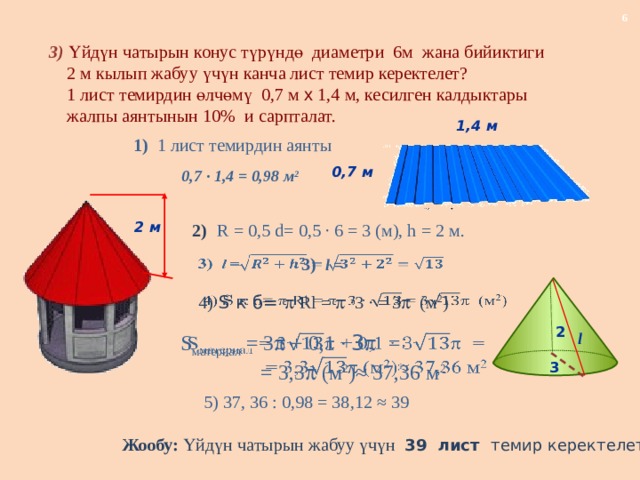
3) Үйдүн чатырын конус түрүндө диаметри 6м жана бийиктиги

2 м кылып жабуу үчүн канча лист темир керектелет?

1 лист темирдин өлчөмү 0,7 м x 1,4 м, кесилген калдыктары

жалпы аянтынын 10% и сарпталат.

1,4 м

1) 1 лист темирдин аянты

0,7 м

0,7 · 1,4 = 0,98 м 2

2 м

2) R = 0,5 d= 0,5 · 6 = 3 (м), h = 2 м.

3) l =

4) S к б=  Rl =  ·3 · = 3  (м 2 )

2

l

S материал = 3  + 0,1 · 3  =

= 3,3  (м 2 )≈ 37,36 м 2

3

5) 37, 36 : 0,98 = 38,12 ≈ 39

Жообу: Үйдүн чатырын жабуу үчүн 39 лист темир керектелет.

№ 4. Конустун түзүүчүсү l , октук кесилишинин

чокусундагы бурчу Конустун толук бетинин аянтын тапкыла.

l ,

Берилди:

Табуу керек:

R=

S т.б =  R( l + R) ,

Чыгаруу:

l

S т.б =  R( l + R)

l

l

l

S т.б =  ( l + )

= 

S т.б =

Жообу:

№ 21. Конустун түзүүчүсү l =16 cм, R=4cм болсо, анда конустун толук бетинин аянтын тапкыла.

Берилди:

l =16 cм, R=4cм

l =16 cм

Табуу керек:

S т.б =  R( l + R)

Чыгаруу:

S т.б =  (16 +4)= 80 

R=4cм

Жообу: 80  см 2

Кесилген конустун беттеринин аянттары:

r – кичине негиздин радиусу

R- чоң негиздин радиусу

l – кесилген конустун түзүүчүсү

S к.б =  l ( r + R)

Кесилген конустун каптал бетинин аянты

негиздеринин айланаларынын узундуктарынын

суммасынын жарым түзүүчүсүнө көбөйткөнгө барабар.

-кичине негизинин аянты

-чоң негизинин аянты

Толук бетинин аянты -

S т.б =+

S т.б =+

№ 8. Кесилген конустун бийиктиги 8 дм, негиздеринин диаметрлери

20дм жана 8 дм. Анын каптал беттеринин аянтын жана

толук бетинин аянтын тапкыла.

20дм,

h =8 дм,

Берилди:

8дм

Табуу керек:

S к.б =  l (r+ R)

Чыгаруу:

10 дм,

l=

S к.б =  l (r+ R)

=  10 (4+10)=140

S т.б =+

8дм

8дм

S т.б = 140  +

6дм

=140  + 16

Жообу:

140 ;

Тапшырма:

• Окуу китебиндеги 229 –бет , №21(3) жана №23 маселени чыгарабыз.
• Конус жана кесилген конустун негизги элементтерин кайталайбыз.

Үйдө олтур!

Байланыш: - Дамира эже

жана - 0773 401 121

E-mail [email protected]