КОУ ВО «ЦЛПДО»
Разработка уроков-консультаций в 11 классе
« Первообразная и интеграл».
Подготовила Л.И. Гоптарь.
-Воронеж-
2020 г.
Цель урока:
обобщение и систематизация знаний.
Задачи урока:
образовательные:
углубление понимания сущности определенного интеграла путем применения его для получения новых знаний;
развитие умений и навыков применять определенный интеграл при решении задач;
воспитательные:
воспитание познавательного интереса к учебному предмету;
воспитание у учащихся культуры мышления;
формирование умений осуществлять самоконтроль;
развивающие:
формирование умений строить доказательства, логическую цепочку рассуждений;
формирование умений проводить обобщение, переносить знания в новую ситуацию.
Структура урока:
1 этап - мотивационно - ориентировочный:
разъяснение целей учебной деятельности учащихся, мотивация учащихся: выйти на результат.
2 этап - подготовительный:
актуализация опорных знаний, необходимых для решения задач.
3 этап - основной:
осмысление последовательности выполнения действий согласно правилу (работа с проговариванием правил); совершенствование или коррекция умений учащихся в зависимости от успешности выполнения предыдущего этапа (кто быстро справился – работает с более сложными заданиями; кто испытывал затруднения – продолжает работать с заданиями стандартного уровня); отчёт учащихся о выполнении заданий.
4 этап – тестирование.
5 этап - заключительный:
подведение общих итогов, инструкция по выполнению дополнительного задания, рефлексия.
Ход урока:
Организационный момент.
На индивидуальных карточках записаны неопределенные
интегралы и их необходимо вычислить.
№1. Вычислить интеграл


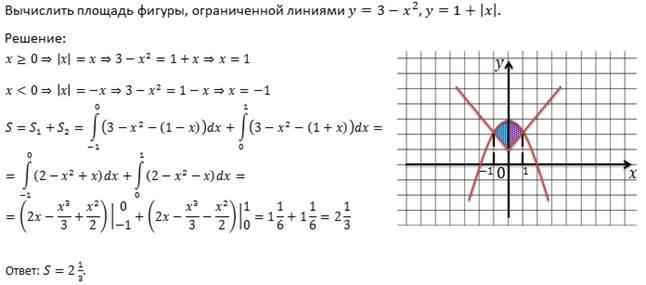
№2. Вычислить площадь фигуры, ограниченной линиями y= x2 - 2x+2 и y= - x2+6
Решение.
Построить фигуру, ограниченную y= x2 - 2x+2 и y= - x2+6
Найти абсциссы точек пересечения графиков данных функций
x 2 - 2x+2 = - x2+6
2 - 2x+2 = - x2+6
2x2 - 2x - 4 =0
x2 – x - 2=0
х1= - 1, х2 = 2
Вычислить площадь





III. Работа с классом. Применение приобретенных знаний, умения и навыков.
Всем известно, что ключ к практике – это теория, нам необходимо вспомнить теоретические основы по теме (фронтальный опрос).
Для этого давайте ответим на следующие вопросы.
Какую функцию можно назвать первообразной для функции f (х) на [а; b] ?
Сформировать основные свойства первообразной.
Как называется операция нахождения первообразной функции?
Как называется действие, обратное интегрированию?
Какие геометрические задания приводят к понятию первообразной?
Какая фигура называется криволинейной трапецией?
Как найти площадь криволинейной трапеции?
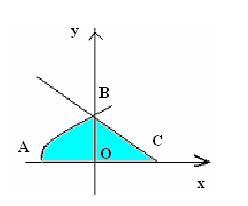
Какие из данных фигур являются криволинейными трапециями?

Запишите площадь заштрихованной фигуры.
Выберите первообразную для функции  .
.
1) 2)
2) 3)
3)
Найдите общий вид первообразных для функции  .
.
1) 2)
2) 3)
3)
Вычислить интегралы:
Запишите в виде определенного интеграла площадь фигуры, ограниченной линиями
y=x2+1, x=1, x=2, y=0
Вычислите площадь заштрихованной фигуры

15.
Найдите площадь криволинейной трапеции, ограниченной линиями:
у=х2-4х+5, у=х+5, y=0, х=-3, х=3.

IV. Провожу тестирование.
1 | Дифференцируемая функция F(x) называется первообразной для функции f(x) на промежутке Х, если в каждой точке этого промежутка… |
| 
| 
| F(x) =f(x)+C | 
|
2 | Правильность интегрирования можно проверить: |
| первообразной | дифференцированием | вычитанием | сложением |
| Операция нахождения неопределённого интеграла от некоторой функции называется… |
| логарифмированием | дифференцированием | интегрированием; | Вычислением предела |
| Чему равен |
| 
| 
| 
| 2х+С |
| Множество всех первообразных функции  имеет вид … имеет вид … |
| 
| 
| 
| 2+ |
| Выберите правильный вариант ответа: … |
| 
| 
| |
|
| Выберите правильный вариант ответа |
| | | 
| |
| Написать правильное продолжение формулы  |
| 
| 
| 
| 
|
| Выберите правильное продолжение решения  |
| 
| 
| 
| 
|
| Написать правильное продолжение формулы  |
| 
| 
| cosx + c | 
|
| Чему равен интеграл  |
| 5cosx +c | 2cosx+c | -10cosx +c | 10cosx +c |
| Множество всех первообразных функции  имеет вид … имеет вид … |
| 
| 
| 
| 
|
| Формула Ньютона-Лейбница: |
| | | | |
V. Из истории.
Символ  ydx был введен немецким математиком Готфридом Лейбницем в 1686 году.
ydx был введен немецким математиком Готфридом Лейбницем в 1686 году.
Существует версия о том, что он букву S, используемую для обозначения суммы писал слегка удлиненной.
Так постепенно и родился новый символ.
Термин интеграл (от латинского integer-целый) был предложен в 1696 году учеником Лейбница - Иоганном Бернулли. Лейбниц, хотя и неохотно согласился с этим. Вероятно, оно происходит от латинскогоintegero, которое переводится, как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования “восстанавливает” функцию, дифференцированием которой получена подынтегральная функция.)
Возникновение задач интегрального исчисления связано с нахождением площадей и объемов.
Ряд задач такого рода был решен математиками древней Греции.
Необходимо было выделить общие идеи, лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно точный алгоритм.
Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известный вам под названием формулы Ньютона - Лейбница.
Как вы думаете, где находит применение интеграл?
А зачем обычному среднестатистическому человеку нужен интеграл?
Все ли мы используем знания, полученные на уроке, где-то в повседневной жизни или в ближайшем будущем?
Поднимите руки, у кого дома есть телевизор; у кого есть сотовый телефон; у кого дома есть компьютер.
Так вот даже обычный сельский житель, который не имеет общего с наукой, в повседневной жизни пользуется знаниями об интеграле.
Естественно, некоторые люди, которые пользуются этими приборами, могут и не знать, как вычисляется интеграл и что это вообще такое.
Но каждый из нас пользуется предметами быта, даже не подозревая, что, чтобы эти приборы работали, какие-то ученые составляли интегральные схемы, проводили исследования.
И в каждом вашем сотовом телефоне находится интегральная схема.
А знаете ли вы?
Что интегралы используются при:
решении задач из области физики;
решении экономических задач (на оптимизацию работы фирмы в условиях конкуренции, расчет о доходности потребительского кредита);
решении социально - демографических задач (математическая модель народонаселения Земли и др.).
«Задача о каше»:
Оля насыпала в цилиндрическую кастрюлю немного пшена и спросила маму: «Сколько нужно налить воды, чтобы получилась вкусная каша?»
«Это очень просто, - ответила мама, – наклони кастрюлю, постучи, чтобы крупа пересыпалась и закрыла ровно половину дна.
Теперь заметь точку на стенке кастрюли у края, до которого поднялась крупа, и зажми ее пальцем.
До этого уровня надо налить воду!» – «Так ведь пшена можно насыпать побольше или поменьше, да и кастрюли бывают разные – широкие узкие», – усомнилась Оля.
«Все равно, мой способ годится в любом случае», - гордо ответила мама».
Доказать:  .
.
С помощью определенного интеграла мы будем в дальнейшем выводить формулы объемов тел вращения.
VI. Подведение итога урока.
Итог урока.
Вывод:
- обобщили знания и отработали навыки решения задач на нахождение первообразных и вычисления интеграла, провели подготовку к ЕГЭ;
- развили чувство самостоятельности и ответственности за качество своих знаний;
- развили навыки самоконтроля, умений анализировать, составлять план или алгоритм учебных действий.
Оценивание:
- За работу по карточкам.
- За активное участие на уроке.
Рефлексия.
Лист рефлексии Фамилия, имя__________________
| № | Вопрос | Ответ ( + или - ) |
| 1 | Комфортно ли вам было на уроке? | . |
| 2 | Поняли ли вы материал урока? | . |
| 3 | Требовалась ли вам помощь: а) учителя б) учебника в) товарища |
. . . |
| 4 | Оцените свою работу на уроке по пятибалльной системе. | . |


VII. Дополнительное задание и инструктаж о ее выполнении.
Задача № 1 Вычислить площадь фигуры, ограниченной линиями: у = х2+1; у = - х2+4х +1.
Построим графики указанных функций в одной системе координат
Найдем пределы интегрирования - абсциссы точек пересечения графиков А и В. Для этого решим уравнение: х2+1= - х2+4х +1  2х2-4х =0
2х2-4х =0  х(х-2)=0
х(х-2)=0  или х=2. Площадь искомой фигуры равна разности двух определённых интегралов на промежутке [0;2]. S=
или х=2. Площадь искомой фигуры равна разности двух определённых интегралов на промежутке [0;2]. S=  = =
= =
= ( +8) = 2
+8) = 2 (кв.ед.) Ответ: 2
(кв.ед.) Ответ: 2 кв.единиц.
кв.единиц.
Задача № 2
Вычислить интеграл:
Лист рефлексии Фамилия, имя__________________
| № | Вопрос | Ответ ( + или - ) |
| 1 | Комфортно ли вам было на уроке? | . |
| 2 | Поняли ли вы материал урока? | . |
| 3 | Требовалась ли вам помощь: а) учителя б) учебника в) соседа по парте? |
. . . |
| 4 | Оцените свою работу на уроке по пятибалльной системе. | . |
_______________________________________________________________________________
Всем спасибо за урок и за хорошую работу на уроке…










 2 - 2x+2 = - x2+6
2 - 2x+2 = - x2+6






 .
. 2)
2) 3)
3)
 .
. 2)
2) 3)
3)

















