Вариант № 11
1. Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Станции | Кировская | Летняя | Балтийская | Нарвская |
| Цифры |
|
|
|
|

На рисунке изображена схема метро города N. Станция Кировская Синей ветки расположена между станциями Яблочная и Заводская. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Яблочная, Восточная, Летняя, Площадь победы, Морская. Красная ветка включает в себя станции Балтийская, Банковская, Морская, Восточная и Нарвская.
Решение. Станция Кировская расположена между станциями Яблочная и Заводская, значит, Кировская отмечена цифрой 3. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Яблочная, Восточная, Летняя, Площадь победы, Морская, следовательно, Летняя отмечена цифрой 2. Красная ветка включает в себя станции Балтийская, Банковская, Морская, Восточная и Нарвская, поэтому Балтийская отмечена цифрой 5, а Нарвская отмечена цифрой 1.
Ответ: 3251.
2. Бригада меняет рельсы на участке между станциями Восточная и Нарвская протяжённостью 16,2 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 600 метров рельсов. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
Решение. Заметим, что станция Нарвская отмечена на схеме цифрой 1. Поскольку бригада меняла по 600 метров рельсов в день, на замену рельс на всём участке ушло 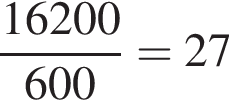 дней. Поскольку работы велись только с понедельника по пятницам, на замену рельс на данном участке ушло
дней. Поскольку работы велись только с понедельника по пятницам, на замену рельс на данном участке ушло  недель, следовательно, необходимо учитывать 5 · 2 = 10 выходных дней. Значит, проезд между указанными станциями был закрыт
недель, следовательно, необходимо учитывать 5 · 2 = 10 выходных дней. Значит, проезд между указанными станциями был закрыт 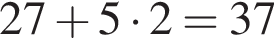 дней.
дней.
Ответ: 37.
3. Территория, находящаяся внутри кольцевой линии, называется Кировским городским районом. Найдите его площадь S (в км2), если длина кольцевой ветки равна 70 км. В ответе укажите значение выражения S · π.
Решение. Сначала найдём радиус окружности:
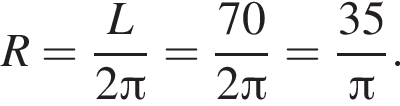
Теперь найдём площадь:
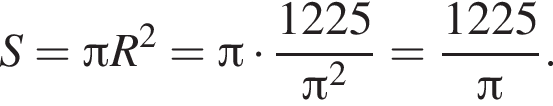
Таким образом, получаем ответ:
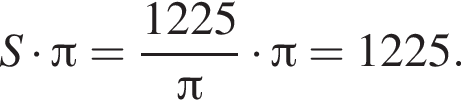
Ответ: 1225.
4. Найдите расстояние (в км) между станциями Яблочная и Кировская, если длина Синей ветки равна 48 км, расстояние от Площади победы до Кировской равно 28 км, а от Заводской до Яблочной — 27 км. Все расстояния даны по железной дороге.
Решение. Расстояние от Кировской до Заводской равняется  км. Расстояние от Площади победы до Яблочной равняется
км. Расстояние от Площади победы до Яблочной равняется  км. Значит, расстояние между станциями Яблочная и Кировская равно
км. Значит, расстояние между станциями Яблочная и Кировская равно  км.
км.
Ответ: 7.
5. Школьник Артём в среднем в месяц совершает 45 поездок в метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Артём уедет из города и неиспользованные карточки обнуляются. Во сколько рублей обойдётся самый дешёвый вариант?
| Количество поездок | Стоимость карточки
(руб.) | Дополнительные условия |
| 1 | 80 | школьникам скидка 15% |
| 10 | 740 | школьникам скидка 10% |
| 30 | 2100 | школьникам скидка 10% |
| 50 | 3200 | нет |
| Не ограничено | 4000 | нет |
Решение. Заметим, что последние два вида карточек можно не рассматривать. Сначала Артём должен купить карточку третьего вида, поскольку
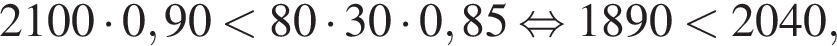
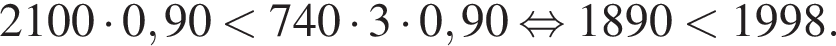
Потом Артём должен купить карточку второго вида, поскольку

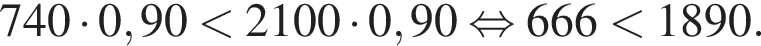
Дальше Артём должен купить пять карточек первого вида, поскольку
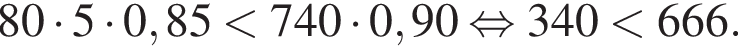
Таким образом, самый дешёвый вариант обойдётся в 
Ответ: 2896.
6. Найдите значение выражения 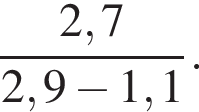
Решение. Вычислим и сократим:
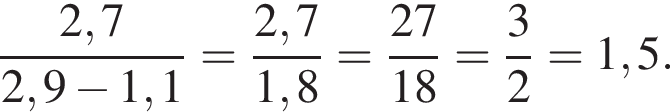
Ответ: 1,5.
7. На координатной прямой отмечено число a.

Найдите наибольшее из чисел a2, a3, a4.
В ответе укажите номер правильного варианта.
1) a2
2) a3
3) a4
4) не хватает данных для ответа
Решение. Заметим, что 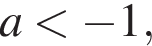 откуда следует, что
откуда следует, что 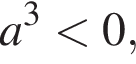
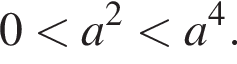 Значит,
Значит, 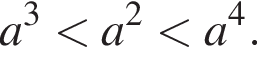 Таким образом, наибольшее из представленных в ответе чисел —
Таким образом, наибольшее из представленных в ответе чисел — 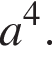
Правильный ответ указан под номером: 3.
8. Найдите значение выражения 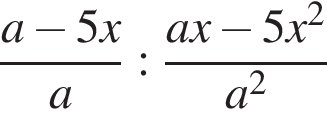 при a = −74, x = −10.
при a = −74, x = −10.
Решение. Упростим выражение:
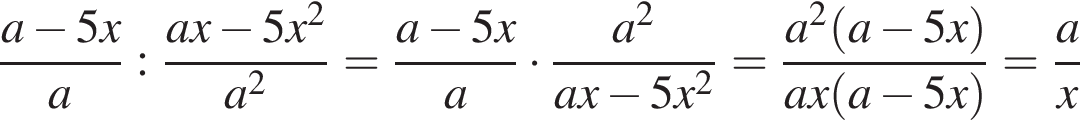
Найдём значение выражения при a = −74, x = −10:
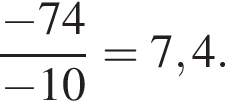
Ответ: 7,4.
9. Найдите корни уравнения 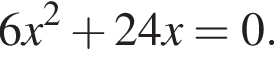
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение. Вынесем общий множитель за скобки:
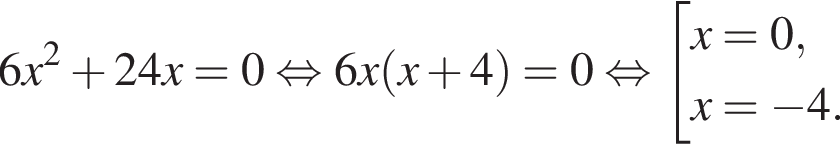
Ответ: -40.
10. В магазине канцтоваров продаётся 200 ручек: 23 красные, 9 зелёных, 8 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет синей или чёрной.
Решение. Найдём количество синих и чёрных ручек: 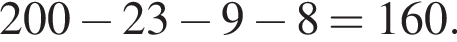 Вероятность того, что будет вытащена синяя или чёрная ручка равна
Вероятность того, что будет вытащена синяя или чёрная ручка равна 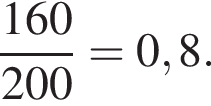
Ответ: 0,8.
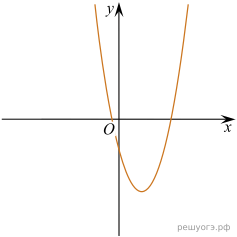
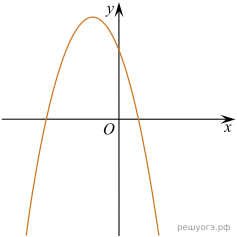
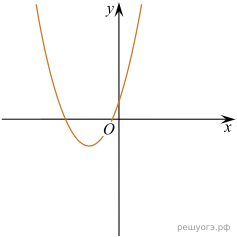
11. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
КОЭФФИЦИЕНТЫ
А) 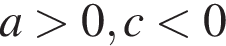
Б) 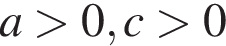
В) 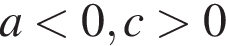
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Решение. Если парабола задана уравнением 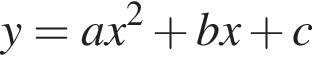 , то: при
, то: при  то ветви параболы направлены вверх, а при
то ветви параболы направлены вверх, а при  — вниз. Значение c соответствует значению функции в точке x = 0. Следовательно, если график пересекает ось ординат выше оси абсцисс, то значение c положительно, если ниже оси абсцисс — отрицательно.
— вниз. Значение c соответствует значению функции в точке x = 0. Следовательно, если график пересекает ось ординат выше оси абсцисс, то значение c положительно, если ниже оси абсцисс — отрицательно.
Таким образом, функциям соответствуют следующие графики: А — 1, Б — 3, В — 2.
Ответ: 132.
12. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C = 6500 + 4000n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец. Ответ дайте в рублях.
Решение. Вычислим:
C = 6500 + 4000 · 12 = 54 500.
Ответ: 54 500.
13. Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.

1) 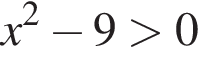
2) 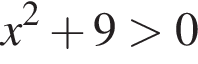
3) 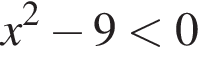
4) 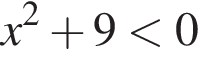
Решение. Решим каждое из неравенств:
1) 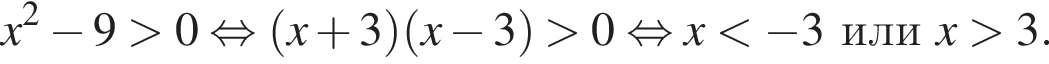
2) 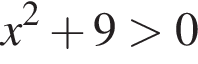 — верно для всех
— верно для всех 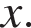
3) 
4) 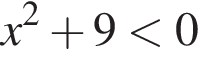 — решений нет.
— решений нет.
Правильный ответ указан под номером 1.
14. Мама договорилась с Димой, что в понедельник он будет учить испанские слова. За первое выученное слово она даст сыну 5 конфет, а за каждое следующее слово на 2 конфеты больше, чем за предыдущее. Сколько конфет Дима получит от мамы в понедельник, если он выучит 12 слов?
Решение. Растущее количество конфет составляет арифметическую прогрессию 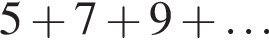 с первым членом a1 = 5, разностью d = 2. Сумму первых 12 членов прогрессии
с первым членом a1 = 5, разностью d = 2. Сумму первых 12 членов прогрессии 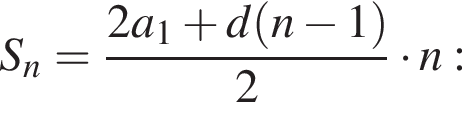
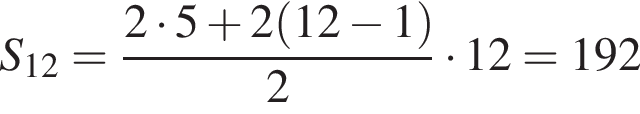 конфеты.
конфеты.
Ответ: 192 конфеты.
15.
Два катета прямоугольного треугольника равны 10 и 24. Найдите гипотенузу этого треугольника.
Решение. По теореме Пифагора в прямоугольном треугольнике сумма квадратов катетов  равна квадрату гипотенузы
равна квадрату гипотенузы 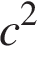 . Таким образом,
. Таким образом,

Ответ: 26
16.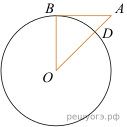
Отрезок AB = 63 касается окружности радиуса 60 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
Решение. Радиус окружности перпендикулярен касательной в точке касания. Из прямоугольного треугольника AOB по теореме Пифагора найдём 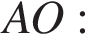
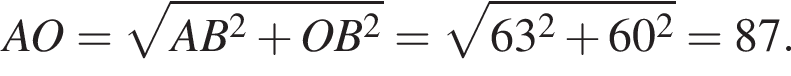
Найдём 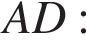

Ответ: 27.
17.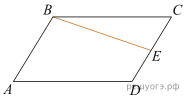
Площадь параллелограмма ABCD равна 8. Точка E — середина стороны CD. Найдите площадь трапеции ABED.
Решение. Диагональ параллелограмма делит его на два равных треугольника, поэтому  Медиана треугольника делит его на два равновеликих треугольника, поэтому
Медиана треугольника делит его на два равновеликих треугольника, поэтому 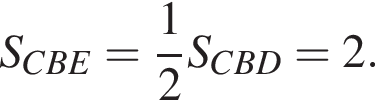 Следовательно,
Следовательно,
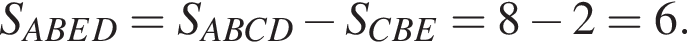
Ответ: 6.
18.  На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
Решение.  Расстояние от точки А до середины отрезка ВС равно четырем сторонам клетки, или 4 см.
Расстояние от точки А до середины отрезка ВС равно четырем сторонам клетки, или 4 см.
Ответ: 4.
19. Какое из следующих утверждений верно?
1) Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти окружности касаются.
2) Вписанные углы окружности равны.
3) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
4) Через любые четыре точки, не принадлежащие одной прямой, проходит единственная окружность.
Решение. Проверим каждое из утверждений.
1) «Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти окружности касаются.» — неверно, если расстояние между центрами двух окружностей равно сумме их радиусов, то эти окружности касаются.
2) «Вписанные углы окружности равны.» — неверно, угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Они равны тогда, когда опираются на одну и ту же дугу.
3) «Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.» — верно, вписанный угол измеряется половиной дуги, на которую он опирается.
4) «Через любые четыре точки, не принадлежащие одной прямой, проходит единственная окружность.» — неверно, некоторые точки могут не попасть на окружность.
Ответ: 3.
20. Решите систему уравнений 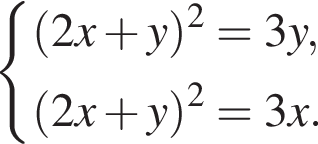
Решение. Последовательно получаем:
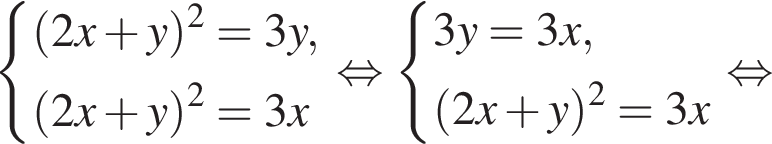
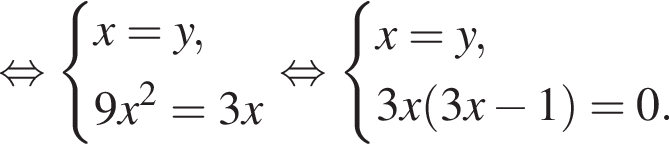
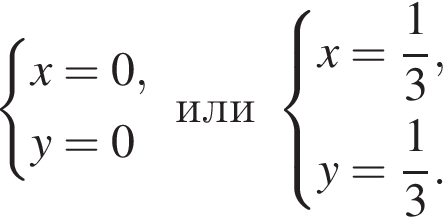
Ответ: (0; 0); 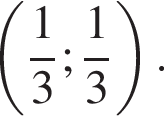
21. На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?
Решение. Заметим, что победителем на выборах окажется Зайцев. Пусть количество голосов, отданных за Зайцева равно x. Тогда за Журавлёва и Иванова вместе отдали  . Процент голосов, отданных за Зайцева
. Процент голосов, отданных за Зайцева 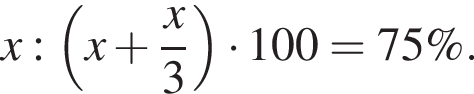
Ответ: 75%.
22. Постройте график функции 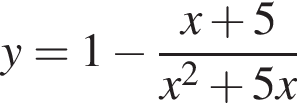 и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.
и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.
Решение. Преобразуем выражение: 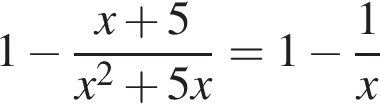 при условии, что
при условии, что 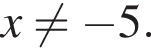
Построим график:

Прямая  не имеет с графиком ни одной общей точки при
не имеет с графиком ни одной общей точки при 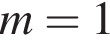 и
и 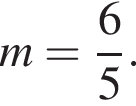
Ответ: 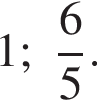
23. Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Решение. 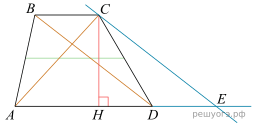 Пусть
Пусть 

 — длина средней линии. Проведём высоту CH и проведём прямую CE, параллельную
— длина средней линии. Проведём высоту CH и проведём прямую CE, параллельную 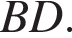 Рассмотрим четырёхугольник
Рассмотрим четырёхугольник 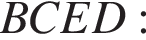
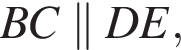
 следовательно, BCED — параллелограмм, откуда
следовательно, BCED — параллелограмм, откуда 
 Рассмотрим треугольник ACE,
Рассмотрим треугольник ACE,  Пусть p — полупериметр треугольника
Пусть p — полупериметр треугольника  Найдём площадь треугольника ACE по формуле Герона:
Найдём площадь треугольника ACE по формуле Герона:


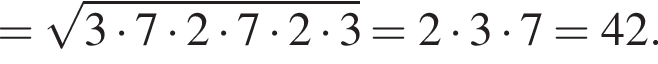
Выразим площадь треугольника ACE как произведение основания AE на высоту CH, откуда найдём 
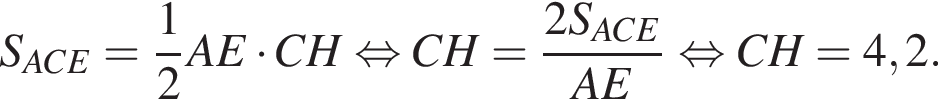
Площадь трапеции равна произведению высоты на полусумму длин оснований: 
Ответ: 42.
Примечание.
Можно не искать высоту трапеции, а заметить, что площади треугольников ABC и CDE равны, так как соответственно равны их основания BC и DE и высоты проведённые к этим основаниям. Тогда 
24. Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD = 15. Докажите, что треугольники CBD и BDA подобны.
Решение.  Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках CBD и ADB имеем:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках CBD и ADB имеем: 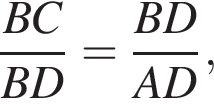 следовательно, эти треугольники подобны по двум парам пропорциональных сторон и углу между ними.
следовательно, эти треугольники подобны по двум парам пропорциональных сторон и углу между ними.
25. В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ = 14, SQ = 4 .
Решение.  Поскольку ∠QPS = ∠QPM = ∠MNQ = ∠QNP (см. рис.), треугольник PQS подобен треугольнику NQP по двум углам (угол при вершине Q общий). Поэтому
Поскольку ∠QPS = ∠QPM = ∠MNQ = ∠QNP (см. рис.), треугольник PQS подобен треугольнику NQP по двум углам (угол при вершине Q общий). Поэтому 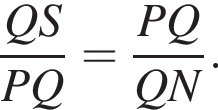
Пусть NS = x. Тогда 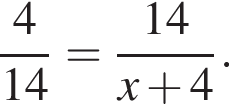
Из этого уравнения находим, что x = 45.
Ответ: 45.
| № задания | ответ |
| 1 | 3251 |
| 2 | 37 |
| 3 | 1225 |
| 4 | 7 |
| 5 | 2896 |
| 6 | 1,5 |
| 7 | 3 |
| 8 | 7,4 |
| 9 | -40 |
| 10 | 0,8 |
| 11 | 132 |
| 12 | 54500 |
| 13 | 1 |
| 14 | 192 |
| 15 | 26 |
| 16 | 27 |
| 17 | 6 |
| 18 | 4 |
| 19 | 3 |
| 20 | 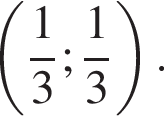 (0; 0) (0; 0)
|
| 21 | 75 |
| 22 | 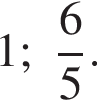
|
| 23 | 42 |
| 24 | - |
| 25 | 45 |








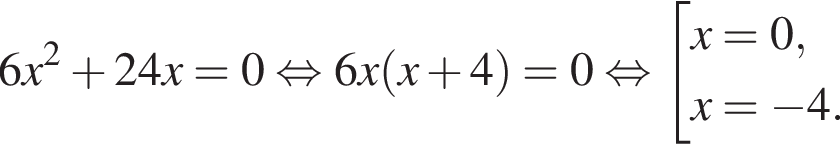


 На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах. Расстояние от точки А до середины отрезка ВС равно четырем сторонам клетки, или 4 см.
Расстояние от точки А до середины отрезка ВС равно четырем сторонам клетки, или 4 см.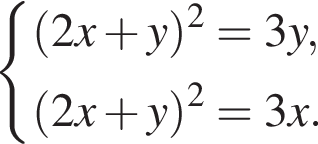
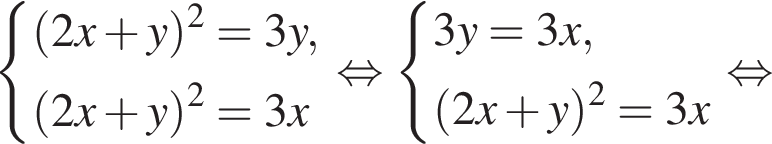
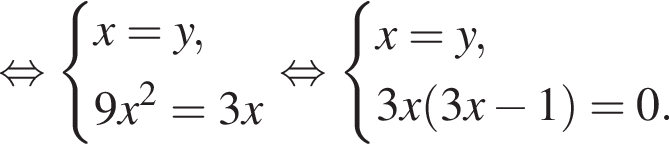
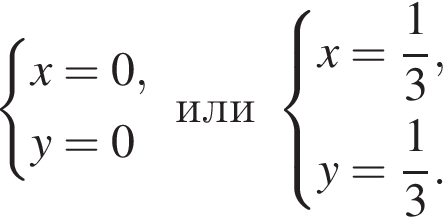

 Пусть
Пусть  Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках CBD и ADB имеем:
Углы CBD и BDA равны, как накрест лежащие при параллельных прямых. В треугольниках CBD и ADB имеем:  Поскольку ∠QPS = ∠QPM = ∠MNQ = ∠QNP (см. рис.), треугольник PQS подобен треугольнику NQP по двум углам (угол при вершине Q общий). Поэтому
Поскольку ∠QPS = ∠QPM = ∠MNQ = ∠QNP (см. рис.), треугольник PQS подобен треугольнику NQP по двум углам (угол при вершине Q общий). Поэтому 



















