19.03.20г. гр. 823 Трехфазная система ЭДС

19.03.20г. гр. 823 «Трехфазная система ЭДС»

Получение трехфазной ЭДС

Под трехфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе на 120°. Гра­фики их мгновенных значений изображены на рис. 1, векторная диаграмма — на рис. 2. Принцип получения трехфазной системы ЭДС иллюстрирует рис. 3. В равномерном магнитном поле с по­стоянной угловой скоростью вращаются три одинаковых жестко скрепленных друг с другом катушки.

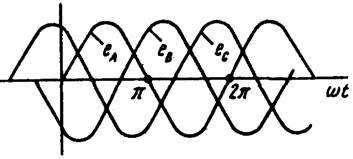
Рисунок 1- Графики мгновенных значений ЭДС

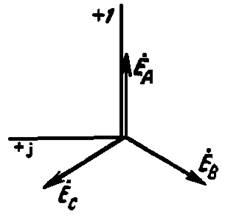
Рисунок 2- Векторная диаграмма ЭДС

Рисунок 3- Принцип получения трехфазной системы ЭДС

Плоскости катушек смещены в пространстве друг относительно друга на 120°. В каждой катушке наводится синусоидальная ЭДС одинаковой амплитуды. По фазе ЭДС катушек сдвинуты на 120°.

Аналогичным путем можно получить двух- и четырехфазную систему ЭДС и более. Наибольшее практическое применение по­лучила трехфазная система.

ЭДС трехфазного генератора рис. 4 обозначают следующим образом: одну из ЭДС — Е_А, отстающую от нее на 120° ЭДС — Е_В, а опере­жающую на 120° — Е_С. Последовательность прохождения ЭДС через одинаковые зна­чения (например, через нулевое значение) называют последова­тельностью фаз.

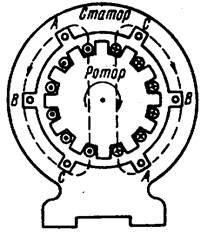
Рисунок 4- Трехфазный генератор

Из-за сдвига на   Т в пространстве имеем три ЭДС:

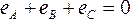
Совокупность ТСЭ, трёхфазной нагрузки и соединительных проводов – трёхфазная цепь.

2. Схемы соединения генератора и нагрузки звездой или треугольником

Трехфазная цепь. Расширение понятия фазы.

Совокуп­ность трехфазной системы ЭДС, трехфазной нагрузки (нагрузок) и соединительных проводов называют трехфазной цепью.

Токи, протекающие по отдельным участкам трехфазных цепей, сдвинуты относительно друг друга по фазе. Под фазой трехфазной цепи понимают участок трехфазной цепи, по которому протекает одинаковый ток. В литературе фазой иногда называют однофазную цепь, входящую в состав многофазной цепи. Под фазой будем также понимать аргумент синусоидально меняющейся величины. Таким образом, в зависимости от рассматриваемого вопроса фаза — это либо участок трехфазной цепи, либо аргумент синусоидально изме­няющейся величины.

Основные схемы соединения трехфазных цепей, определе­ние линейных и фазовых величин.

Существуют различные способы соединения обмоток генератора с нагрузкой. Самым неэкономич­ным способом явилось бы соединение каждой обмотки генератора с нагрузкой двумя проводами, на что потребовалось бы шесть сое­динительных проводов. В целях экономии обмотки трехфазного ге­нератора соединяют в звезду или треугольник. При этом число соединительных проводов от генератора к нагрузке уменьшается с шести до трех или до четырех.

На электрической схеме трехфазный генератор принято изобра­жать в виде трех обмоток, расположенных друг к другу под углом 120°. При соединении звездой одноименные зажимы (например, концы х, у, z.) трех обмоток объединяют в одну точку (рис. 5), которую называют нулевой точкой генератора О. Обмотки генера­тора обозначают буквами А, В, С; буквы ставят: А —у начала первой, В — у начала второй и С — у начала третьей фазы.

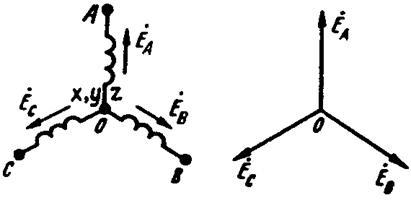
Рисунок 5- Соединение генератора по схеме «звезда»

При соединении обмоток генератора треугольником (рис. 6) конец первой обмотки генератора соединяют с началом второй, конец второй — с началом третьей, конец третьей — с началом пер­вой. Геометрическая сумма ЭДС в замкнутом треугольнике равна нулю. Поэтому если к зажимам А, В, С не присоединена нагрузка, то по обмоткам генератора не будет протекать ток.

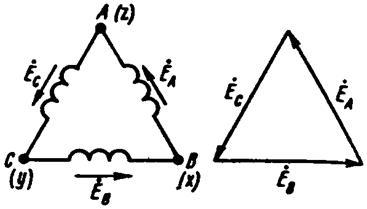
Рисунок 6- Соединение генератора по схеме «зтреугольник»

Пять простейших способов соединения трехфазного генератора с трехфазной нагрузкой изображены на рис. 7 — 10.

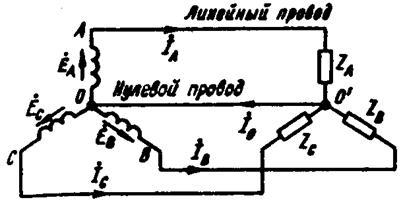
Рисунок 7- Соединение «звезда»- «звезда» с нулевым проводом

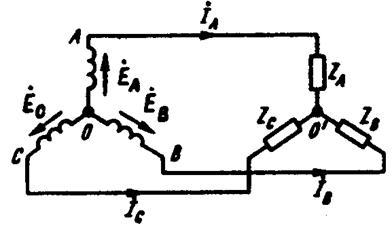
Рисунок 8- Соединение «звезда»- «звезда» без нулевого провода

Точку, в которой объединены три конца трехфазной нагрузки при соединении ее звездой, называют нулевой точкой нагрузки и обозначают О'. Нулевым проводом называют провод, соединяю­щий нулевые точки генератора и нагрузки. Ток нулевого провода назовем I₀. Положительное направление тока возьмем от точки О' к точке О.

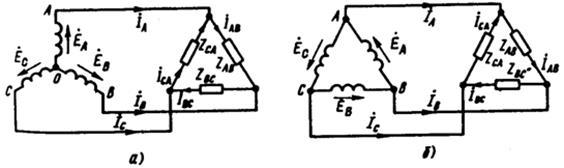
Рисунок 9- Соединения «звезда»- «треугольник» и «треугольник»- «треугольник»

Провода, соединяющие точки А, В, С генератора с нагрузкой, называют линейными.

Схему рис. 7 называют звезда — звезда с нулевым проводом; схему рис. 8—звезда—звезда без нулевого провода; схему рис.9, а — звезда — треугольник; схему рис. 9, б — треуголь­ник — треугольник; схему рис. 10 — треугольник — звезда.

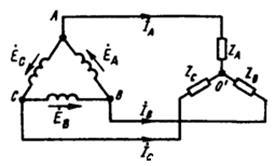
Рисунок 10- Соединение «треугольник»- «звезда»

Текущие по линейным проводам токи называют линейными; их обозначают I_A, I_B, I_C. Условимся за положительное направление токов принимать направление от генератора к нагрузке. Модули линейных токов часто обозначают I_Л (не указав никакого дополни­тельного индекса), особенно тогда, когда все линейные токи по мо­дулю одинаковы.

Напряжение между линейными проводами называют линейным и часто снабжают двумя индексами, например U_AB (линейное на­пряжение между точками А и В); модуль линейного напряжения обозначают U_Л.

Каждую из трех обмоток генератора называют фазой генерато­ра; каждую из трех нагрузок — фазой нагрузки; протекающие по ним токи—фазовыми токами генератора Iф или соответственно нагрузки, а напряжения на них — фазовыми напряжениями Uф.

Преимущества трехфазных систем.

Широкое распростра­нение трехфазных систем объясняется главным образом тремя основными причинами:

1) передача энергии на дальние расстояния трехфазным током экономически более выгодна, чем переменным током с иным числом фаз;

2) элементы системы—трехфазный синхронный генератор, трехфазный асинхронный двигатель и трехфазный трансформа­тор — просты в производстве, экономичны и надежны в работе;

3) система обладает свойствами неизменности значения мгно­венной мощности за период синусоидального тока, если нагрузка во всех трех фазах трехфазного генератора одинакова.

Расчет трехфазных цепей

Трехфазные цепи являются разновидностью цепей синусоидального тока, и потому расчет и исследование процессов в них производят теми же методами и при­емами, которые рассматривались в цепях однофазного синусоидального тока. Для цепей трехфазного тока применим также символический метод расчета и можно стро­ить векторные, топографические и круговые диаграммы.

Аналитический расчет трехфазных цепей рекомендуется сопро­вождать построением векторных и топографических диаграмм. Векторные диаграммы облегчают нахождение углов между токами и напряжениями, делают все соотношения более наглядными и помогают находить ошибки при аналитическом расчете, если по­следние возникнут.

Соединение звезда — звезда с нулевым проводом.

Если нулевой провод в схеме рис. 7 обладает весьма малым сопротив­лением, то потенциал точки О' практически равен потенциалу точ­ки О; точки О' и О фактически представляют собой одну точку. При этом в схеме образуются три обособленных контура, через которые проходят токи

По первому закону Кирхгофа ток в нулевом проводе равен гео­метрической сумме фазовых токов:

Если   , то нагрузка равномерная, и   =0.

Если нагрузка равномерная, то   .

Если   (   ), то нагрузка неравномерная   . Но   , т. к. есть нулевой провод.

При неравномерной нагрузке фаз ток I₀ в общем случае не равен нулю.

При наличии в нулевом проводе некоторого сопротивления рас­чет схемы производят методом узловых потенциалов.

Соединение «звезда – звезда» без нулевого провода.

Условимся комплексное число   по модулю равное единице обозначать через «   » и называть его оператором трёхфазной системы.

Три вектора   образуют симметричную трёхфазную систему.

Умножение какого – либо вектора на   поворачивает его без изменения модуля на   против часовой стрелки, умножение на   – на  против часовой стрелки (или на   по часовой стрелке).

 ; 

По методу двух узлов:

Если нагрузка равномерная   :

 , и напряжение в каждой фазе нагрузки равно соответствующей ЭДС (   ;   ;

 ).

Если нагрузка неравномерная, то   .

 и т.д.

Таким образом, при трёхфазной трёхпроводной линии несимметричной нагрузки;

Мощность при соединении «звезда».

 (   если есть сопротивление нулевого провода).

При симметричной нагрузке   , т. к.

Если нагрузка равномерная, то   и 

 , т. е.   (аналогично для   ).

 , т. к.   , а 

 .

Соединение нагрузки в «треугольник».

Линейные токи:   ;

 ;   .

 При равномерной нагрузке   , т. к.

Мощность при соединении «треугольник»

Если нагрузка симметричная, то 

Измерение мощности проводится, как при соединении «звезда» без нулевого провода.

Расчет активной, реактивной и полной мощности в трехфазных цепях

Активной мощностью (часто просто мощностью) трехфазной систе­мы называется сумма активных мощностей всех фаз источника энер­гии, равная сумме активных мощностей всех фаз приемника.

В симметричной трехфазной системе, т. е. в системе с симметричны­ми генератором и приемником, при любой схеме их соединений для каждой фазы мощности источника энергии и приемника одинаковые. В этом случае Р = ЗР_ф и для каждой из фаз справедлива формула ак­тивной мощности синусоидального тока:

где у - угол сдвига фаз между фазными напряжением и током.

Заменив действующие значения фазных тока и напряжения линей­ными при соединении фаз источника энергии и приемника звездой и треугольником, получим одно и то же выражение для активной мощности симметричной трехфазной системы:

 (2)

В промышленных установках приемники обычно симметричные или почти симметричные, т. е. мощность может быть вычислена по (2).

В общем случае реактивной мощностью трехфазной системы назы­вается сумма реактивных мощностей всех фаз источника энергии, равная сумме реактивных мощностей всех фаз приемника. Реактивная мощ­ность симметричной трехфазной системы

 (3)

или после замены действующих значений фазных тока и напряжения линейными

 (4)

Полная мощность симметричной трехфазной системы

 (5)

Комплексной мощностью трехфазной системы называется сумма комплексных мощностей всех фаз источника энергии, равная сумме комплексных мощностей всех фаз приемника.

Мощность в трехфазной цепи можно определить по формулам   ,   , где   - комплекс напряжения i-той фазы («a», «b» или «c» для схемы «звезда» и «ab», «bc» или «ca» для схемы «треугольник»);   - сопряженный комплекс тока i-той фазы.

К расчёту (определению) трёхфазной мощности нагрузки методом двух ваттметров.

При переходе к средней мощности и действующим значениям тока и напряжения имеем:

По разности показаний двух ваттметров можно определить реактивную мощность трёхфазной системы.

Пусть активно – индуктивная нагрузка симметрична.

Угол   между векторами   и   равен

 .

Угол   между векторами   и   равен

 .

Тогда   ; 

 , т. е.   .

   При симметричной нагрузке мощность   можно измерить одним ваттметром.

 .

Способы повышения коэффициента мощности

Многие электротехнические устройства синусоидального тока (фазо­вращатели, двигатели и др.) имеют сильные магнитные поля. У таких устройств велика реактивная (индуктивная) составляющая тока, т. е. большой положительный угол сдвига фаз φ между напряжением и током, что ухудшает их коэффициент мощности cos φ, а значит, и коэффициент мощности промышленного предприятия в це­лом. Низкое значение cos φ приводит к неполному использованию гене­раторов, линий передачи и другого электротехнического оборудова­ния, которое бесполезно загружается реактивным (индуктивным) током. Эта составляющая тока обусловливает также увеличение потерь электрической энергии во всех токопроводящих частях (обмотках двигателей, трансформаторов, генераторов, проводах линий переда­чи и др.).

Чтобы увеличить значение cos φ , необходимо включить параллельно приемнику со значительной реактивной (индуктивной) составляющей тока батарею конденсаторов. Реактивный (емкостный) ток батареи конденсаторов компенсирует реактивный (индуктивный) ток при­емника.

Представим приемник в виде эквивалентной схемы замещения пас­сивного двухполюсника. Компенсация реактивного (ин­дуктивного) тока приемника (тока нагрузки) I_р.н. при помощи бата­реи конденсаторов показана на векторной диаграмме, из которой видно, что коэффициент мощности после включения батареи конденсаторов увеличивается: cosφ cosφ_H. В большинстве слу­чаев допустима неполная компенсация сдвига фаз.

Если ток нагрузки I_н и коэффициент мощности приемника cosφ_H известны и задано требуемое значение cosφ после компенсации, то не­обходимое значение емкости конденсатора можно определить при по­мощи векторной диаграммы токов, из которой следует, что

откуда

где Р - активная мощность приемника.

Улучшение cosφ посредством включения конденсаторов называется искусственным улучшением коэффициента мощности в отличие от ес­тественного улучшения, получаемого при полном использовании мощ­ности двигателей и установке таких двигателей (синхронных), у кото­рых реактивный ток очень мал.

В трехфазных цепях для компенсации реактивной мощности на ходе приемников включаются батареи конденсаторов по схеме треугольник (как правило на высокой стороне трансформатора).

Домашнее задание:

I. Начало первой обмотки при соединении обмоток генератора треугольником соединяется:

1. с началом второй;

1. концом третьей;

2. концом второй;

3. началом третьей;

4. концом третьей.

II. Фазой называют:

1. аргумент синуса;

2. часть многофазной цепи;

3. фазу в начальный момент времени;

4. оба определения ответов 1 и 2 правильны;

5. разность начальных фаз переменных величин.

III. Симметричная нагрузка соединена звездой. Линейное напряжение 380 В. Фазное напряжение равно:

1. 220 В;

2. 380 В;

3. 250 В;

4. 127 В;

5. 660 В.

IV. Лампы накаливания с U_Н = 127 В включают в трехфазную сеть с линейным напряжением 220 В. Схема включения ламп:

1. звездой;

2. треугольником;

3. звезда с нулевым проводом;

4. лампы нельзя включать в сеть;

5. для ответа недостаточно данных.

V. Действующее значение трехфазной ЭДС при изменении направления вращения катушек:

1. изменится;

2. увеличится в три раза;

3. уменьшится в три раза;

4. изменится на  3;

5. не изменится.

VI. Ток в нулевом проводе четырехпроводной цепи:

1. не может равняться нулю;

2. может равняться нулю;

3. всегда равен нулю;

4. всегда больше нуля;

5. всегда меньше нуля.

VII. В симметричной трехфазной цепи U_Ф= 220 В, I_Ф = 5 A, cos  = 0,8. Активная мощность цепи равна:

1. 1,1 кВт;

2. 0,88 кВт;

3. 2,2 кВт;

4. 2,64 кВт;

5. 5, 28 кВт.

VIII. Если при прочих условиях изменить скорость вращения обмоток, то изменятся:

1) амплитуды и начальные фазы;

частота и начальные фазы;

1. ЭДС и начальные фазы;

2. частота и амплитуды;

3. ЭДС и амплитуды.

IX. Сумма токов фаз равна нулю при отсутствии нулевого провода:

1. не всегда;

2. всегда;

3. зависит от условий;

4. зависит от числа проводов — 3 или 4;

5. зависит от 2-фазы.

X. Обмотки, показанные на рис. 3.1, соединены:

1. звездой;

2. треугольником;

3. последовательно;

4. параллельно;

5. другим способом.Рис. 3.1.

XI. При симметричной нагрузке, соединенной треугольником, U_Л= 380В. Фазное напряжение равно:

1) 220В;

2) 127 В;^-

3) 660 В;

4) 250 В;

5) 380 В.

XII. Дано: U_Л= 220 В; I_Л = 5 A; cos  = 0,8. Трехфазная цепь симметричная. Активная мощность цепи составляет:

1. 1,1 кВт;

2. 1,14 кВт;

3. 1,52 кВт;

4. 2,2 кВт;

5. 2,06 кВт.

Литература:

Березкина Т.Ф. и др. Задачник по общей электротехнике с основами электроники [Текст]: Учеб. Пособие для студ. неэлектротехн. спец. средних спец. учеб. заведений / Т.Ф. Березкина, Н.Г. Гусев, В.В. Масленников. – 3-е изд., стер. - М.: Высшая школа, 2002. -380 с.: ил.,№ 6.4 стр.134-135).

• Лоторейчук Е.А. Расчет электрических и магнитных цепей и полей. Решение задач [Текст]: учебное пособие. - М.:ИД «ФОРУМ»: ИНФРА-М, 2012. – 272 с. – (Профессиональное образование), № 6.9, 6.10 стр.167-168.

1. Решить задачи по расчету трехфазных цепей:

• Березкина Т.Ф. и др. Задачник по общей электротехнике с основами электроники [Текст]: Учеб. Пособие для студ. неэлектротехн. спец. средних спец. учеб. заведений / Т.Ф. Березкина, Н.Г. Гусев, В.В. Масленников. – 3-е изд., стер. - М.: Высшая школа, 2002. -380 с.: ил. (№ 6.13, 6.16, 6.24, стр.137-140).