Просмотр содержимого документа
«28.15.Ещё пример задания»
Ещё пример задания:
Каково наибольшее целое число X, при котором истинно высказывание
(50 X·X) → (50 (X+1)·(X+1))
Решение (вариант 1):
это операция импликации между двумя отношениями  и
и 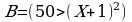
попробуем сначала решить неравенства
 ,
, 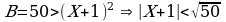
обозначим эти области на оси X:

на рисунке фиолетовые зоны обозначают область, где истинно выражение 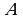 , голубая зона – это область, где истинно
, голубая зона – это область, где истинно 
вспомним таблицу истинности операции «импликация»:
| A | B | A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
согласно таблице, заданное выражение истинно везде, кроме областей, где  и
и 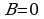 ; область истинности выделена зеленым цветом
; область истинности выделена зеленым цветом
поэтому наибольшее целое число, удовлетворяющее условию – это первое целое число, меньшее  , то есть, 7
, то есть, 7
таким образом, верный ответ – 7 .
| Возможные проблемы: в этом примере потребовалось применить знания не только (и не столько) из курса информатики, но и умение решать неравенства нужно не забыть правила извлечения квадратного корня из обеих частей неравенства (операции с модулями) |
Решение (вариант 2, преобразование выражения):
сначала можно преобразовать импликацию, выразив ее через «ИЛИ» и «НЕ»:

это значит, что выражение истинно там, где  или
или 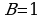
дальнейшие действия точно такие же, как и в варианте 1.
Решение (вариант 3, математический):
это операция импликации между двумя отношениями  и
и 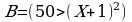
пусть 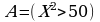 – истинно, тогда, с учетом того, что
– истинно, тогда, с учетом того, что 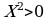 , находим, что
, находим, что 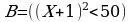 – ложно, таким образом, импликация
– ложно, таким образом, импликация 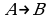 ложна
ложна
следовательно, импликация может быть истинной только при 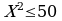 ; поскольку в этом случае высказывание
; поскольку в этом случае высказывание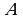 ложно, то
ложно, то 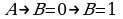 при любом
при любом 
максимальное целое значение X, при котором 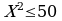 , равно 7
, равно 7
таким образом, верный ответ – 7 .







 и
и 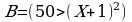
 ,
, 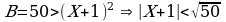

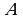 , голубая зона – это область, где истинно
, голубая зона – это область, где истинно 
 и
и 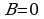 ; область истинности выделена зеленым цветом
; область истинности выделена зеленым цветом , то есть, 7
, то есть, 7
 или
или 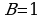
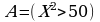 – истинно, тогда, с учетом того, что
– истинно, тогда, с учетом того, что 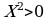 , находим, что
, находим, что 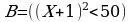 – ложно, таким образом, импликация
– ложно, таким образом, импликация 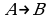 ложна
ложна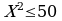 ; поскольку в этом случае высказывание
; поскольку в этом случае высказывание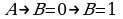 при любом
при любом 









