Ещё пример задания:
Сколько различных решений имеет система уравнений
X1 X2 X3 = 1
X2 X3 X4 = 1
...
X8 X9 X10 = 1
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение (последовательное подключение уравнений):
рассмотрим сначала все решения первого уравнения; его левая части истинна, когда X1=1 (при этом X2 и X3 могут быть любыми), а также когда X1=0 и X2=X3=1:
| X1 | X2 | X3 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
заметим, что первое и второе уравнения связаны через последние две переменных, в данном случае это X2 и X3
пусть i – число переменных в уравнениях; введем обозначения:
Ki – количество решений, в которых последние две переменные принимают
значения (0,0)
Li – количество решений, в которых последние две переменные принимают
значения (0,1)
Mi – количество решений, в которых последние две переменные принимают
значения (1,0)
Ni – количество решений, в которых последние две переменные принимают
значения (1,1)
из таблицы видим, что K3=1, L3=1, M3=1 и N3=2
теперь подключаем второе уравнение; посмотрим, к чему приводят разные комбинации последних двух переменных:
| X1 | X2 | X3 | X4 |
| 0 | 1 | 1 | 0 |
| 1 |
| 1 | 0 | 0 | × |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 |
| 1 | 1 | 1 | 0 |
| 1 |
находим, что
комбинация (0,0) не дает ни одного решения,
комбинация (0,1) дает одно решение, и при этом (X3,X4)=(1,1)
комбинация (1,0) дает два решения, причем (X3,X4)=(0,0) или (0,1)
комбинация (1,1) дает два решения, причем (X3,X4)=(1,0) или (1,1)
из предыдущего пункта делаем вывод, что
Ki+1 = Mi (комбинация (0,0) появилась из (1,0) на предыдущем шаге)
Li+1 = Mi (комбинация (0,1) появилась из (1,0) на предыдущем шаге)
Mi+1 = Ni (комбинация (1,0) появилась из (1,1) на предыдущем шаге)
Ni+1 = Li+Ni (комбинация (1,1) появляется из (0,1) и (1,1))
используя эти рекуррентные формулы, заполняем таблицу для i=4,…,10
| i | Ki | Li | Mi | Ni | Всего |
| 3 | 1 | 1 | 1 | 2 | 5 |
| 4 | 1 | 1 | 2 | 3 | 7 |
| 5 | 2 | 2 | 3 | 4 | 11 |
| 6 | 3 | 3 | 4 | 6 | 16 |
| 7 | 4 | 4 | 6 | 9 | 23 |
| 8 | 6 | 6 | 9 | 13 | 34 |
| 9 | 9 | 9 | 13 | 19 | 50 |
| 10 | 13 | 13 | 19 | 28 | 73 |
таким образом, ответ: 13 + 13 + 19 + 28 = 73 решения.
Решение (метод отображений1, решение А.Н. Носкина):
построим таблицу, в которой переберем все варианты x1, x2, x3, поскольку в первом логическом уравнении три переменных, то таблица будет иметь 8 строк (8 = 23); уберем из таблицы (желтая заливка) такие значения x2 и x3, при которых первое уравнение не имеет решения.
| x1 | x2 | x3 |
| 0 | 0 | 0 |
| 1 |
| 1 | 0 |
| 1 |
| 1 | 0 | 0 |
| 1 |
| 1 | 0 |
| 1 |
анализируя таблицу, строим правило отображения пар переменных
(например, паре x1x2 = 00 не соответствуют ни одной пары x2x3 , и наоборот паре x1x2 = 01 соответствует только пара x3x4 = 11).
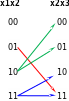
Заполняем таблицу, вычисляя количество пар переменных, при котором система имеет решение.
|
| x1x2 | x2x3 | x3x4 | x4x5 | x5x6 | x6x7 | x7x8 | x8x9 | x9x10 |
| 00 | 0 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 |
| 01 | 1 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 |
| 10 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 19 |
| 11 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 19 | 28 |
таким образом, ответ: 13 + 13 + 19 + 28 = 73 решения.
1� Метод отображений предложен Ел.А. Мирончик и Ек.А. Мирончик (http://kpolyakov.spb.ru/download/b15mirn.zip).


















