
Графический метод решения системы уравнений с двумя переменными

Алгоритм решения системы уравнений графическим способом
1 . Приводим оба уравнения к виду линейной функции y = k x + m.
2. Составляем расчётные таблицы для каждой функции.
3. Строим графики функций в одной координатной плоскости.
4. Определяем число решений:
- Если прямые пересекаются, то одно решение пара чисел (х ; у) – координаты точки пересечения;
- Если прямые параллельны, то нет решений;
- Если прямые совпадают, то бесконечно много решений.
5. Записываем ответ.
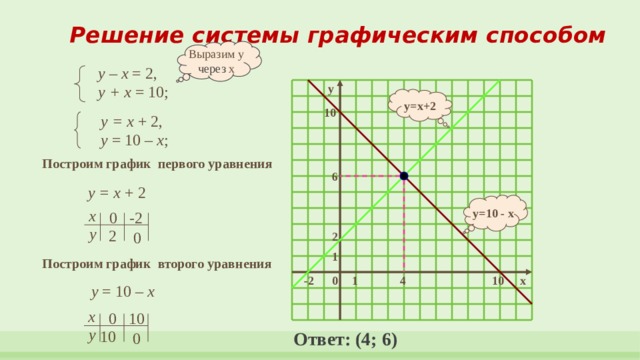
Решение системы графическим способом
Выразим у
через х
у – х = 2,
у + х = 10;
y
y=x+2
10
у = х + 2,
у = 10 – х ;
Построим график первого уравнения
6
у = х + 2
y=10 - x
х
-2
0
у
2
0
2
1
Построим график второго уравнения
x
10
4
0
1
-2
у = 10 – х
х
0
10
у
10
Ответ: (4; 6)
0
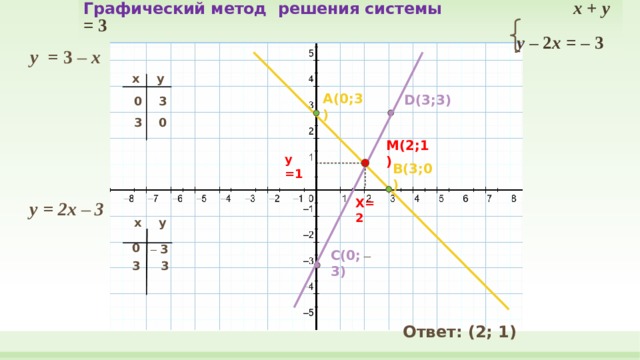
Графический метод решения системы x + y = 3 y – 2 x = – 3
у = 3 – x
x
y
A(0;3)
D(3;3)
3
0
0
3
M(2;1)
у =1
B(3;0)
X=2
у = 2x – 3
y
x
0
– 3
C(0; – 3)
3
3
Ответ: (2; 1)
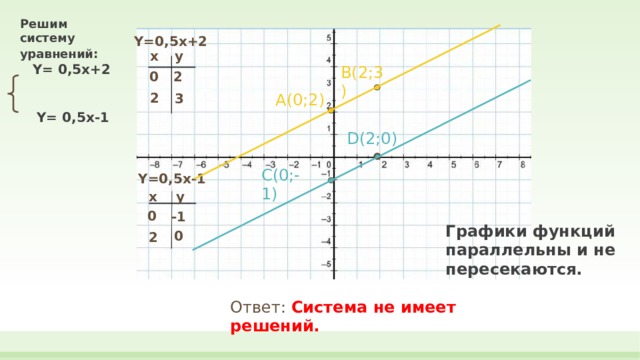
Решим систему уравнений: Y= 0,5x+2 Y= 0,5x-1
Y=0,5x+2
x
y
B(2;3)
0
2
2
A(0;2)
3
D(2;0)
C(0;-1)
Y=0,5x-1
y
x
0
-1
Графики функций параллельны и не пересекаются.
0
2
Ответ: Система не имеет решений.
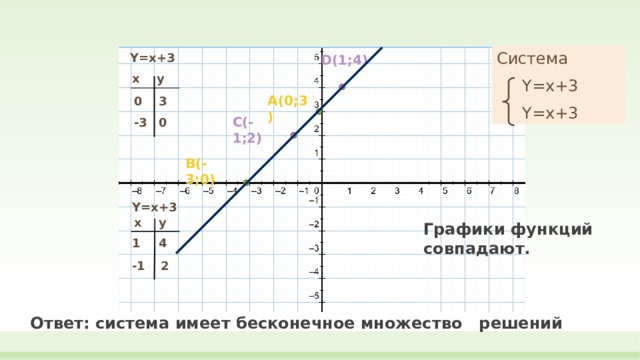
Система
Y=x+3
Y=x+3
Y=x+3
D(1;4)
x
y
A(0;3)
3
0
C(-1;2)
0
-3
B(-3;0)
Y=x+3
y
x
Графики функций совпадают.
4
1
2
-1
Ответ: система имеет бесконечное множество решений
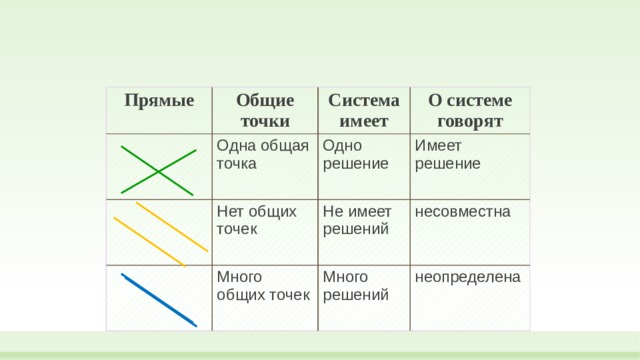
Прямые
Общие точки
Одна общая точка
Система имеет
Нет общих точек
Одно решение
О системе говорят
Много общих точек
Имеет решение
Не имеет решений
Много решений
несовместна
неопределена
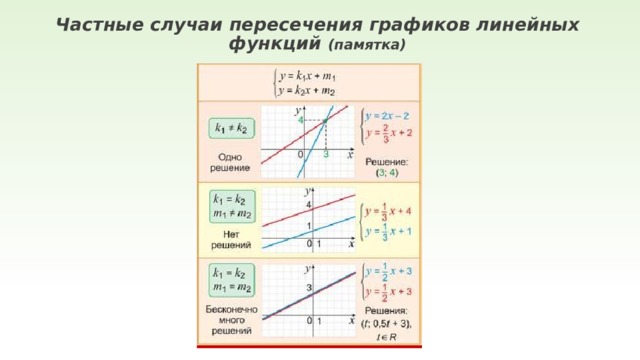
Частные случаи пересечения графиков линейных функций (памятка)


































