7-sinf, To'g'riburchakli uchburchak xossalari.

_{Fani: Geometriy}a Sinf: 7-b Sana: 19.02

I.Mavzu. To’g’ri burchakli uchburchakning xossalari

Darsning maqsadi: : To’g’ri burchakli uchburchakning xossalari haqida tushuncha berish, misollar keltirish, ularning har biriga izoh berish.

Darsning ta’limiy ahamiyati: O’quvchilarni geometriya faniga qiziqtirish, mavzu to’g’risida tushuncha berish, bilim va malakasini oshirish.

Darsning tarbiyaviy ahamiyati: O’quvchilarni mustaqillikka o’rgatish, erkin fikrlash qobiliyatini rivojlantirish.

Darsning kasbga yo’naltiruvchi maqsadi: O’quvchilarga To’g’ri burchakli uchburchakning xossalari haqida tushuncha va bilimlarni singdirish.

Darsning uslubi: savol-javob, munozara.

Darsning ko’rgazmali qurollari: darslik, doska, bo’r, tarqatma materiallar, jadvallar, geometrik shakllar.

1.Darsning borishi: O’tilgan mavzuni takrorlash.

2.Tashkiliy qism: Salomlashish. Covid-19 dan ehtiyot bo’ling. Qo’llaringizni tez-tez sovunlab yuvib turing. Xona derazalarini ochib shamollatib turing. 2m masofa saqlansin.Ko’chaga chiqqanizda maska taqish esingizdan chiqmasin.

To’g’ri, o’tkir va o’tmas burchaklar

Ta’rif. Kattaligi 90^o bo’lgan burchak to’g’ri burchak, to’g’ri burchakdan kichik bo’lgan burchak o’tkir burchak, to’g’ri burchakdan katta va yoyiq burchakdan kichik

bo’lgan burchak o’tmas burchak deb ataladi (91-rasm)

Stol sirtining tomonlari orasidagi burchak, futbol maydonining burchaklari kabilar to’g’ri burchakdir.

Uchburchakli chizg’ichlarning bitta burchagi to’g’ri burchak bo’lsa, qolgan ikkita burchagi o’tkir burchaklardir.

Oldingi mavzuda uchburchakli chizg’ichlar yordamida 105^o, 120^o, 135^o, 150^o li burchaklarning ham yasalishini o’rgandingiz. Bu burchaklar o’tmas burchaklardir.

Masala (185). Aylana 2:3:4 kabi nisbatda uch bo’lakka bo’lingan. Ularga tiralgan markaziy burchaklarning o’tkir – o’tmasligini ayting.

Yechilishi. Aylana yoyi 2 : 3 : 4 ( - gradus kattaligi) kabi nisbatda uch bo’lakka bo’lingan bo’lsa, 2 + 3 + 4 = 360^o ifoda o’rinli bo’ladi. Undan 9 = 360^o yoki  = 40^o ekanligi kelib chiqadi. Demak, bo’laklardan kichigi 2 = 80^o, ikkinchisi 3 = 120^o va uchinchisi 4 = 160^o bo’lib, ularga mos ravishda tiralgan burchaklarning birinchisi o’tkir, qolgan ikkitasining biri o’tmas burchaklardir.

3.Yangi mavzu bayoni:

Bitta burchagi To’g’ri ya’ni 900 bo4lgan uchburchakni To’g’ri burchakli uchburchak deb atagan edik. Bunday uchburchakda To’g’ri burchak qarshisidagi tomon gipotenuza, qolgan ikki tomon esa katetlar deb ataladi. To4g4ri burchakli uchburchak boshqa uchburchaklardan farqli alohida xossalarga ega.

1-xossa. To’g’ri burchakli uchburchakning qolgan ikkita burchagi o’tkir bo’lib, ularning yig’indisi 90⁰ ga teng.

Haqiqatan, uchburchak ichki burchaklari yig’indisi 1800 ga teng, To’g’ri burchagi esa 90⁰ ga teng. Shuning uchun, uning qolgan ikki burchagi yig’indisi 180⁰ - 90⁰ = 90⁰ ga teng bo’ladi.

Bunda ularning o’tkir burchak bo’lishi kelib chiqadi.

Xossa isbotlandi.

1-masala. To’g’ri burchakli uchburchakning 30⁰ li burchagi qarshisidagi kateti gipotenuzasining yarmiga teng.

ABC To’g’ri burchakli uchburchakda ACB = 90⁰ va ABC = 30⁰ bo’lsin. U holda 1-xossaga ko’ra BAC = 60⁰ bo’ladi.

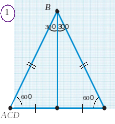1-rasmda ko’rsatilgandek qilib berilgan uchbur- chakka teng BCD uchburchakni yasaymiz. Natijada, hamma burchaklari 60⁰ ga teng bo’lgan ABD uchburchakka ega bo4lamiz.

Demak, ABD uchburchak teng tomonli. Xususan,

AB = AD bo’ladi. Lekin,

AD = AC + CD = 2AC.

Shunday qilib, AB = 2AC, ya’ni AC = ^AB.

Teskari xossa ham o’rinli: ²

2-xossa. To’g’ri burchakli uchburchakning katetlaridan biri gipotenuzaning yarmiga teng bo’lsa, u katet qarshisidagi burchak 30⁰ li bo’ladi.

Mashq. 2-xossani isbotlang.

2-masala. ABC t To’g’ri burchakli uchburchakda C — to’g’ri burchak, AB = 12 va CD=DB bo4lsa, CD ni toping (2-rasm).

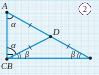Yechilishi. Berilganiga ko’ra CDB O teng yonli uchburchak (2-rasm).

 ACD = α,  DCB = β desak,  α + β = 90⁰. Boshqa burchaklar, α + β = 90⁰ (1-xossaga ko’ra).

A = α.

2

Bu masalani yechish davomida AD=DB va AD = CD tengliklarni ham hosil qildik. Bu aslida ixtiyoriy To’g’ri i burchakli uchburchak uchun ham o’rinlidir, chunki bu tengliklarni keltirib chiqarishda AB ning uzunligi nechaga tengligidan foydalanmadik. Bu quyidagi xossasini anglatadi.

3-xossa. To’g’ri burchakli uchburchakning gipotenuzaga tushirilgan medianasi gipotenuzaning yarmiga teng.

4. Yangi mavzuni mustahkamlash:

6*. Teng yonli to’g’ri burchakli uchburchakning gipotenuzasiga tushirilgan balandlik gipotenuzaning yarmiga tengligini korsating.

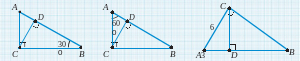
7. a) c =? b) a =? c) x =?

8. a) AB=20, AD=? b) AB =18, BD =? c) BD =?

1. To’g’ri burchakli uchburchakning gipotenuzaga tushirilgan medianasi 8 sm. Agar uchburchakning bir burchagi 600 ga teng bo4lsa, bu burchakka yopishgan tomonlarni toping.

2. To’g’ri burchakli uchburchakning bitta o’tkir burchagi ikkinchisidan 2 marta katta. Uning kichik tomoni 6 sm bo’lsa, katta tomonini toping.

5. Darsga yakun yasash va baholash – darsning maqsadini yana bir bor eslatish va unga qanchalik erishilganligini o’quvchilar bilan birgalikda aniqlash. O’quvchilarning mavzu bo’yicha savollariga javob berish, ulaming o’zlashtirganlik darajasini aniqlash, darsning asosiy lahzalarini qayd qilish. Darsda faol qatnashgan o’quvchilarni tilga olish va baholash;

6. Uyga vazifa:

Internet tarmog’idan uchburchaklar to’g’risida qiziqarli faktlar yig’ib kelish.

Savol, masala va topshiriqlar

1. To’g’ri burchakli uchburchakning tomonlari qanday nomlanadi?

2. To’g’ri burchakli uchburchakning o4tkir burchaklari yig’indisi nimaga teng?

3. To’g’ri burchakli uchburchakning burchaklaridan birortasi o4tmas bo4lishi mumkinmi?

4. To’g’ri burchakli uchburchakning nechta balandligi bor?

5. 300 li burchak qarshisidagi katet bilan gipotenuza orasida qanday bog’lanish bor?

Tasdiqlayman

Olmazor tumani 11-maktab

Direktori. N.Aripova

Toshkent shahar

Olmazor tumani

11-maktab Matematika fani o’qituvchisi

Jumaniyozova Ayimdjan Allaberganovnaning

Geometriya fanidan

“To’g’ri burchakli uchburchakning xossalari “

mavzusida tayyorlagan dars ishlanmasi

Toshkent

2020-2021 o’quv yili