749 рск 20.04.2020

20.04.2020 Расчет колонн.

С теоретической точки зрения расчет центрально-сжатого элемента, каковым является колонна, или стойка в ферме, настолько прост, что даже неудобно об этом говорить. Достаточно разделить нагрузку на расчетное сопротивление стали, из которой будет изготавливаться колонна - все. В математическом выражении это выглядит так:

F = N/R_y (1.1)

где

F - требуемая площадь сечения колонны, см²

N - сосредоточенная нагрузка, прилагаемая к центру тяжести поперечного сечения колонны, кг;

R_y - расчетное сопротивление металла растяжению, сжатию и изгибу по пределу текучести, кг/см². Значение расчетного сопротивления можно определить по соответствующей таблице.

Как видим, уровень сложности задачи относится ко второму, максимум к третьему классу начальной школы. Однако на практике все далеко не так просто, как в теории, по ряду причин:

1. Приложить сосредоточенную нагрузку точно к центру тяжести поперечного сечения колонны можно только теоретически. В реальности нагрузка всегда будет распределенной и еще будет некоторый эксцентриситет приложения приведенной сосредоточенной нагрузки. А раз есть эксцентриситет, значит есть продольный изгибающий момент действующий в поперечном сечении колонны.

2. Центры тяжести поперечных сечений колонны расположены на одной прямой - центральной оси, тоже только теоретически. На практике из-за неоднородности металла и различных дефектов центры тяжести поперечных сечений могут быть смещены относительно центральной оси. А это значит, что расчет нужно производить по сечению, центр тяжести которого максимально удален от центральной оси, из-за чего эксцентриситет действия силы для этого сечения максимальный.

3. Колонна может иметь не прямолинейную форму, а быть немного изогнутой в результате заводской или монтажной деформации а это значит, что поперечные сечения в средней части колонны будут иметь наибольший эксцентриситет приложения нагрузки.

4. Колонна может быть установлена с отклонениями от вертикали, а это значит, что вертикально действующая нагрузка может создавать дополнительный изгибающий момент, максимальный в нижней части колонны, а если точнее, в месте крепления к фундаменту, впрочем это актуально, только для отдельно стоящих колонн.

5. Под действием приложенных к ней нагрузок колонна может деформироваться, а это значит, что опять появится эксцентриситет приложения нагрузки и как следствие дополнительный изгибающий момент.

6. В зависимости от того, как именно закреплена колонна, зависит значение дополнительного изгибающего момента внизу и в средней части колонны.

Все это приводит к появлению продольного изгиба и влияние это изгиба при расчетах нужно как-то учитывать.

Естественно, что рассчитать вышеуказанные отклонения для конструкции, которая еще только проектируется, практически невозможно - расчет будет очень долгим, сложным, а результат все равно сомнительным. А вот ввести в формулу (1.1) некий коэффициент, который бы учел вышеизложенные факторы, очень даже можно. Таким коэффициентом является φ - коэффициент продольного изгиба. Формула, в которой используется данный коэффициент, выглядит так:

F = N/φR (1.2)

Значение φ всегда меньше единицы, это означает, что сечение колонны всегда будет больше, чем если просто посчитать по формуле (1.1), это я к тому, что сейчас начнется самое интересное и помнить, что φ всегда меньше единицы - не помешает. Для предварительных расчетов можно использовать значение φ в пределах 0,5-0,8. Значение φ зависит от марки стали и гибкости колонны λ:

λ = l_ef/i (1.3)

где

l_ef - расчетная длина колонны. Расчетная и реальная длина колонны - разные понятия. Расчетная длина колонны зависит от способа закрепления концов колонны и определяется с помощью коэффициента μ:

l_ef = μl (1.4)

где

l - реальная длина колонны, см;

μ - коэффициент, учитывающий способ закрепления концов колонны. Значение коэффициента можно определить по следующей таблице:

Таблица 1. Коэффициенты μ для определения расчетных длин колонн и стоек постоянного сечения (согласно СНиП II-23-81 (1990))

Как видим, значение коэффициента μ изменяется в несколько раз в зависимости от способа закрепления колонны и тут главная сложность в том, какую расчетную схему выбрать. Если не знаете, какая схема закрепления соответствует Вашим условиям, то принимайте значение коэффициента μ=2. Значение коэффициента μ=2 принимается в основном для отдельно стоящих колон, наглядный пример отдельно стоящей колонны - фонарный столб. Значение коэффициента μ=1-2 можно принимать для колонн навесов, на которые опираются балки без жесткого крепления к колонне. Данную расчетную схему можно принимать, когда балки навеса будут не жестко крепиться к колоннам и когда балки будут иметь относительно большой прогиб. Если на колонну будут опираться фермы, жестко прикрепленные к колонне сваркой, то можно принимать значение коэффициента μ=0,5-1. Если между колоннами будут диагональные связи, то можно принимать значение коэффициента μ=0,7 при нежестком креплении диагональных связей или 0,5 при жестком креплении. Однако такие диафрагмы жесткости не всегда бывают в 2 плоскостях и потому использовать такие значения коэффициента нужно осторожно. При расчете стоек ферм используется коэффициент μ=0,5-1 в зависимости от метода закрепления стоек.

Значение коэффициента гибкости приблизительно показывает отношение расчетной длины колонны к высоте или ширине поперечного сечения. Т.е. чем больше значение λ, тем меньше ширина или высота поперечного сечения колонны и соответственно тем больший запас по сечению потребуется при одной и той же длине колонны, но об этом чуть позже.

Теперь когда мы определили коэффициент μ, можно вычислить расчетную длину колонны по формуле (1.4), а для того, чтобы узнать значение гибкости колонны, нужно знать радиус инерции сечения колонны i:

 (1.5)

где I - момент инерции поперечного сечения относительно одной из осей, и тут начинается самое интересное, потому как в ходе решения задачи мы как раз и должны определить необходимую площадь сечения колонны F, но этого мало, оказывается, мы еще должны знать значение момента инерции. Так как мы не знаем ни того, ни другого, то решение задачи выполняется в несколько этапов.

На предварительном этапе обычно принимается значение λ в пределах 90-60, для колонн с относительно небольшой нагрузкой можно принимать λ = 150-120 (максимальное значение для колонн - 180, значения предельной гибкости для других элементов можно узнать по таблице 19* СНиП II-23-81 (1990). Затем по Таблице 2 определяется значение коэффициента гибкости φ:

Таблица 2. Коэффициенты продольного изгиба φ центрально-сжатых элементов.

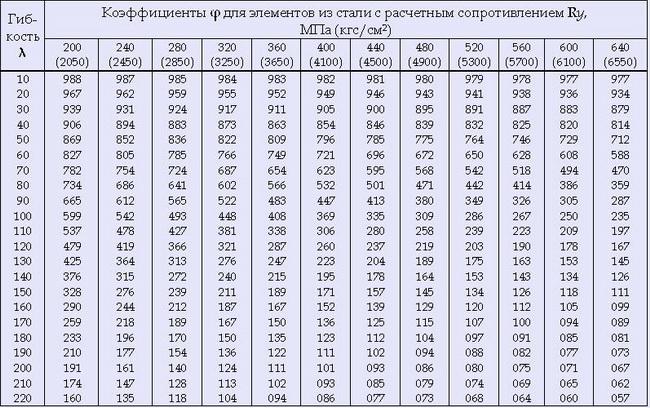
Примечание: значения коэффициента φ в таблице увеличены в 1000 раз.

После этого определяется требуемый радиус инерции поперечного сечения, путем преобразования формулы (1.3):

i = l_ef/λ (1.6)

По сортаменту подбирается прокатный профиль с соответствующим значением радиуса инерции. В отличие от изгибаемых элементов, где сечение подбирается только по одной оси, так как нагрузка действует только в одной плоскости, в центрально сжатых колоннах продольный изгиб может произойти относительно любой из осей и потому чем ближе значение I_z к I_y, тем лучше, другими словами наиболее предпочтительны профили круглого или квадратного сечения. Ну а теперь попробуем определить сечение колонны на основе полученных знаний.