8 класс Геометрия 19.11.20 Теория. Площадь многоугольника. ссылка на видеоурок https://youtu.be/qGREwu2nqiQ

19.11.2020г.

Геометрия

8 а/б класс. Ссылка на видеоурок https://youtu.be/qGREwu2nqiQ

Тема урока: Площадь многоугольника.

В учебнике эту тему можешь прочитать на странице 117, п. 48, п. 49, п. 50.

Открой тетрадь и запиши число на полях и «Классная работа».

Ниже запиши тему урока.

Сегодня мы поговорим о понятии площади многоугольника, о свойствах площадей. Рассмотрим, как находить площадь прямоугольника, площадь квадрата.

Самые важные моменты теории этой темы запиши в тетрадь.

Понятие площади многоугольника. Основные свойства площадей

Разберем следующую ситуацию. Вы дома вместе с родителями решили сделать ремонт: оклеить стены, перестелить пол. Какую помощь вы можете оказать до покупки нужных материалов? Верно, в первую очередь нужно вычислить общую площадь стен и пола в комнате. Затем высчитать количество рулонов обоев для оклейки стен и только после всех подсчетов ехать в магазин.

Площадь многоугольника– это величина той части плоскости, которую занимает многоугольник. Для измерения площадей используют единицы измерения. За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков.

Т ак, единица измерения площади - квадратный сантиметр – это квадрат со стороной равной 1 сантиметру, квадратный метр – это квадрат со стороной 1 метр.

Также единицами измерения площади являются квадратный миллиметр, квадратный дециметр. Употребляются и такие единицы площади, как 1 гектар, 1 ар. 1 гектар – это площадь квадрата со стороной 100 м, 1 ар – квадрата со стороной 10 м. 1 ар часто называю соткой. Говорят: «дачный участок имеет 6 соток».

Площадь любого многоугольника выражается положительным числом. Это число показывает, сколько раз единица измерения и ее части укладываются в данном многоугольнике.

Выделим основные свойства площадей многоугольников:

1.Равные многоугольники имеют равные площади.

2.Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Площадь квадрата и площадь прямоугольника

Помимо основных свойств площадей можно выделить еще одно свойство -

3. Площадь квадрата равна квадрату его стороны.

Если сторону квадрата обозначить через а, то формула запишется S = а².

Рассмотрим теорему о вычислении площади прямоугольника.

Теорема: Площадь прямоугольника равна произведению его смежных сторон.

Д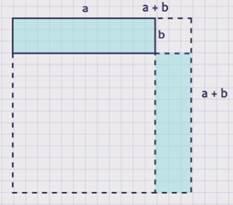 окажем это утверждение.

Дано: прямоугольник со сторонами а и в и площадью S.

Нужно доказать, что S = ав.

Доказательство: достроим прямоугольник до квадрата со стороной а + в, тогда по третьему свойству площадь этого квадрата будет равна (а + в)² .

С другой стороны построенный квадрат состоит из двух прямоугольников со сторонами а и в и площадью S, и двух квадратов c площадями а² и в². По второму свойству площадь квадрата равна сумме площадей этих фигур: двух прямоугольников и двух квадратов, а именно:

(а + в)² = S + S + а² + в², или

а² + 2ав + в² =2S + а² + в², отсюда получаем

S = ав.

Теорема доказана.

Решение задачи по теме урока

Решим задачу.

Задача: Как изменится площадь прямоугольника, если одну пару противоположных сторон увеличить в три раза, а другую уменьшить в три раза?

Р ешение:Пусть дан прямоугольник со сторонами а и в и площадью S1 = ав. После изменения сторон прямоугольник будет иметь одну пару противоположных сторон 3а, а другую 1/3в. Вычислим площадь S2 этого прямоугольника, для этого умножим 3а на 1/3в, имеем:

S2 = 3а · 1/3в = ав = S1.

Ответ: площадь прямоугольника не изменится.