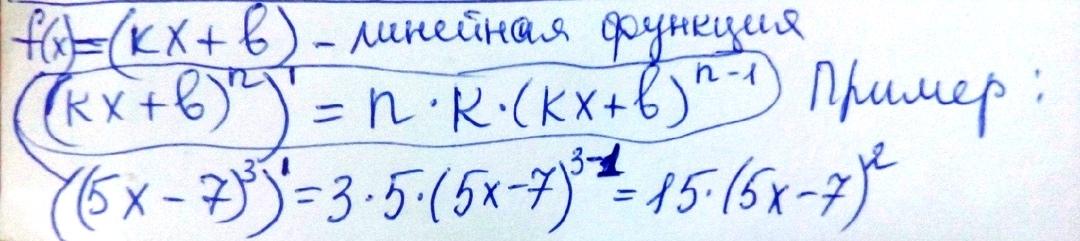916/з, 1-ая пара: "Задачи на нахождение наибольшего и наименьшего значения функции."

Определение производной.

Производная функции это отношение приращения функции к приращению аргумента при бесконечно малом приращение аргумента.

Приращением в математике называют изменение.

То, насколько изменился аргумент (x) при продвижении вдоль оси Ox, называется приращением аргумента и обозначается Δx.

То, насколько изменилась функция (высота) при продвижении вперед вдоль оси Ox на расстояние Δx, называется приращением функции и обозначается Δf.

Итак, производная функции f(x) – это отношение Δf к Δx при Δx→0.

Обозначаем производную той же буквой, что и функцию, только со штрихом сверху справа: f '(x)

или просто f '

Элементарными функциями называют степенные, показательные, логарифмические, тригонометрические функции и их различные комбинации. ( спишите формулы!)

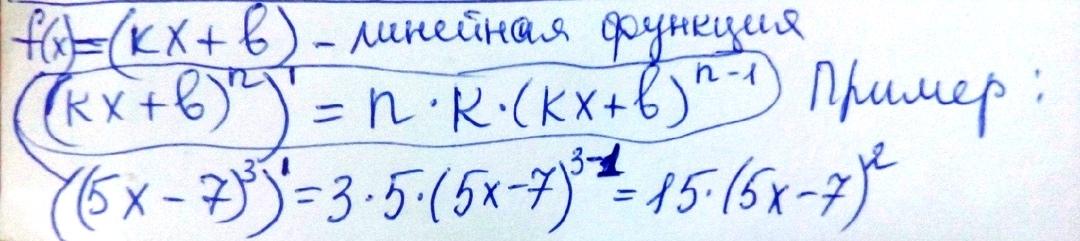
А бывает ли производная равна нулю?

Конечно. Производная постоянной функции (константы) равна нулю: C` = 0,  C(любое число) = const

Правила дифференцирования.

Задачи на нахождение наибольшего и наименьшего значения функции.

Решение 1):

Шаг 1: Найдем значение функции на концах отрезка [-4;3]:

Шаг 2:Найдем ее значения в тех критических точках, которые принадлежат интервалу [-4;3]:

Для этого, сначала найдем производную функции:

Приравняем найденную производную к нулю:

Решим полученное уравнение(найдем корни):
в данном случае у нас получилось квадратное уравнение, решим его с помощью дискриминанта: а=6, b=6, c= -36,
Полученные корни

Интервалу [-4;3] принадлежат обе критические точки поэтому подставим их в функцию и посчитаем значения:

Шаг 3: Из чисел 64, -27, 81,-44 наибольшее 81, наименьшее -44.

Ответ: Наибольшее значение функции равно 81, наименьшее равно -44.

Решение 2):

Шаг 1: Найдем значение функции на концах отрезка [-2;1]:

Шаг 2:Найдем ее значения в тех критических точках, которые принадлежат интервалу [-2;1]:

Для этого, сначала найдем производную функции:

Приравняем найденную производную к нулю:

Решим полученное уравнение(найдем корни):
в данном случае у нас получилось квадратное уравнение, решим его с помощью дискриминанта: а=6, b=6, c= -36,
Полученные корни

На интервале [-2; 1] критических точек нет.

Шаг 3: Из чисел 68 и -31 наибольшее 68, наименьшее -31.

Ответ: Наибольшее значение функции равно 68, наименьшее равно -31.

Задание:
1) Найти наибольшее и наименьшее значения функции на отрезке :

;

2) Найти наибольшее и наименьшее значения функции на отрезке :

;