5
МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Министерство образования Саратовской области
Комитет по образованию администрации
Энгельсского муниципального района
МОУ "ООШ с. Квасниковка"
| РАССМОТРЕНО Руководитель ШМО _______________________ Лукьянович О.Д. Протокол № 1 от «___» 08 2024 г.
| СОГЛАСОВАНО Заместитель директора по УВР ________________________ Планская Е.В. _____от «____» 2024 г | УТВЕРЖДЕНО Директор ________________________ Филатова Ю.В. Приказ № ____ от «01» 09 2024 г.
|
АДАПТИРОВАННАЯ РАБОЧАЯ ПРОГРАММА
для детей ОВЗ вариант 7.1
учебного курса «Алгебра»
для обучающихся 9 класса
Энгельс 2024
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Адаптированная рабочая программа по алгебре для учащихся с задержкой психического развития вариант 7.1 для 9 класса составлена на основе адаптированной основной общеобразовательной программы основного общего образования с учётом рекомендаций ПМПК и на основе учебника «Алгебра, 9 класс/ Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и другие, издательства «Просвещение» в соответствии с действующими законодательными и нормативными актами Российской Федерации, регионального и муниципального уровней.
Нормативно-правовой и документальной адаптированной рабочей программы являются:
- Федеральный закон от 29.12.2012 №273-ФЗ «Об образовании в Российской Федерации» (в действующей редакции);
- Федерального государственного образовательного стандарта основного общего образования (Приказ Минпросвещения России от 31.05.2021 г. № 287, зарегистрирован Министерством юстиции Российской Федерации 05.07.2021 г., рег. номер 64101);
- Примерная адаптированная основная образовательная программа основного общего образования обучающихся с задержкой психического развития (одобрена решением федерального учебно-методического объединения по общему образованию, протокол от 18 марта 2022г. №1/22);
- Примерная рабочая программа основного общего образования по предмету «Математика», с учетом распределенных по классам проверяемых требований к результатам освоения Адаптированной основной образовательной программы основного общего образования обучающихся с задержкой психического развития;
- Порядок организации и осуществления образовательной деятельности по основным общеобразовательным программам - образовательным программам начального общего, основного общего, среднего общего образования, утвержденный приказом Министерства просвещения Российской Федерации от 22.03.2021 №115;
- Постановление Главного государственного санитарного врача Российской Федерации от 29.12.2010 №189 «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» (с изменениями на 29.06.2011);
- Постановление Главного государственного санитарного врача Российской Федерации от 11.03.2003 №13 «Об утверждении СанПиН 2.4.1201-03 «Гигиенические требования к устройству, содержанию, оборудованию и режиму работы специализированных учреждений для несовершеннолетних, нуждающихся в социальной реабилитации»;
- Приказ Минпросвещения России от 21.09.2022 № 858 (ред. От 21.02.2024) "Об утверждении федерального перечня учебников, допущенных к использованию при
реализации имеющих государственную аккредитацию образовательных программ
начального общего, основного общего, среднего общего образования организациями, осуществляющими образовательную деятельность и установления предельного срока использования исключенных учебников" (Зарегистрировано в Минюсте России 01.11.2022 № 70799)
Адаптированная рабочая программа по алгебре для обучающихся с ЗПР - это образовательная программа, адаптированная для обучения данной категории обучающихся с учетом особенностей их психофизического развития, индивидуальных возможностей, обеспечивающая коррекцию нарушений развития и социальную адаптацию.
Алгебра является одним из опорных курсов основной школы: она обеспечивает изучение других дисциплин, как естественнонаучного, так и гуманитарного циклов, её освоение необходимо для продолжения образования и в повседневной жизни. Развитие у обучающихся научных представлений о происхождении
и сущности алгебраических абстракций, способе отражения математической наукой явлений и процессов в природе и обществе, роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения и качеств мышления, необходимых для адаптации в современном цифровом обществе. Изучение алгебры естественным образом обеспечивает развитие умения наблюдать, сравнивать, находить закономерности, требует критичности мышления, способности аргументированно обосновывать свои действия и выводы, формулировать утверждения. Освоение курса алгебры обеспечивает развитие логического мышления обучающихся: они используют дедуктивные и индуктивные рассуждения, обобщение и конкретизацию, абстрагирование и аналогию. Обучение алгебре предполагает значительный объём самостоятельной деятельности обучающихся, поэтому самостоятельное решение задач естественным образом является реализацией деятельностного принципа обучения.
В структуре программы учебного курса «Алгебра» основной школы основное место занимают содержательно-методические линии: «Числа и вычисления»; «Алгебраические выражения»; «Уравнения и неравенства»; «Функции». Каждая из этих содержательно-методических линий развивается на протяжении трёх лет изучения курса, естественным образом переплетаясь и взаимодействуя с другими его линиями. В ходе изучения курса обучающимся приходится логически рассуждать, использовать теоретико-множественный язык. В связи с этим целесообразно включить в программу некоторые основы логики, пронизывающие все основные разделы математического образования и способствующие овладению обучающимися основ универсального математического языка. Таким образом, можно утверждать, что содержательной и структурной особенностью курса «Алгебра» является его интегрированный характер.
Содержание линии «Числа и вычисления» служит основой для дальнейшего изучения математики, способствует развитию у обучающихся логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых для повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием представлений о действительном числе. Завершение освоения числовой линии отнесено к старшему звену общего образования.
Содержание двух алгебраических линий – «Алгебраические выражения» и «Уравнения и неравенства» способствует формированию у обучающихся математического аппарата, необходимого для решения задач математики, смежных предметов и практико-ориентированных задач. В основной школе учебный материал группируется вокруг рациональных выражений. Алгебра демонстрирует значение математики как языка для построения математических моделей, описания процессов и явлений реального мира. В задачи обучения алгебре входят также дальнейшее развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, и овладение навыками дедуктивных рассуждений. Преобразование символьных форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству.
Содержание функционально-графической линии нацелено на получение школьниками знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов и явлений в природе и обществе. Изучение этого материала способствует развитию у обучающихся умения использовать различные выразительные средства языка математики — словесные, символические, графические, вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
На изучение учебного курса «Алгебра» отводится 102 часа в год, 3 часа в неделю.
СОДЕРЖАНИЕ ОБУЧЕНИЯ
9 КЛАСС
Числа и вычисления
Действительные числа
Рациональные числа, иррациональные числа, конечные и бесконечные десятичные дроби. Множество действительных чисел; действительные числа как бесконечные десятичные дроби. Взаимно однозначное соответствие между множеством действительных чисел и координатной прямой.
Сравнение действительных чисел, арифметические действия с действительными числами1.
Измерения, приближения, оценки
Размеры объектов окружающего мира, длительность процессов в окружающем мире.
Приближённое значение величины, точность приближения. Округление чисел. Прикидка и оценка результатов вычислений.
Уравнения и неравенства
Уравнения с одной переменной
Линейное уравнение. Решение уравнений, сводящихся к линейным.
Квадратное уравнение. Решение уравнений, сводящихся к квадратным. Биквадратное уравнение. Примеры решения уравнений третьей и четвёртой степеней разложением на множители.
Решение дробно-рациональных уравнений.
Решение текстовых задач алгебраическим методом.
Системы уравнений
Уравнение с двумя переменными и его график. Решение систем двух линейных уравнений с двумя переменными. Решение систем двух уравнений, одно из которых линейное, а другое — второй степени. Графическая интерпретация системы уравнений с двумя переменными.
Решение текстовых задач алгебраическим способом.
Неравенства
Числовые неравенства и их свойства.
Решение линейных неравенств с одной переменной. Решение систем линейных неравенств с одной переменной. Квадратные неравенства. Графическая интерпретация неравенств и систем неравенств с двумя переменными.
Функции
Квадратичная функция, её график и свойства. Парабола, координаты вершины параболы, ось симметрии параболы.
Графики функций: y = kx, y = kx + b, y = x2,
y = 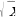 , y =
, y = 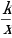 и их свойства.
и их свойства.
Числовые последовательности
Определение и способы задания числовых последовательностей
Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена.
Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых n членов.
Изображение членов арифметической и геометрической прогрессий точками на координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ УЧЕБНОГО ПРЕДМЕТА «АЛГЕБРА» НА УРОВНЕ ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ
Личностные результаты:
мотивация к обучению алгебры и целенаправленной познавательной деятельности;
повышение уровня своей компетентности через практическую деятельность, требующую математических знаний, в том числе умение учиться у других людей;
способность осознавать стрессовую ситуацию, быть готовым действовать в отсутствие гарантий успеха;
способность обучающихся с ЗПР к осознанию своих дефицитов и проявление стремления к их преодолению;
способность к саморазвитию, умение ставить достижимые цели;
умение различать учебные ситуации, в которых можно действовать самостоятельно, и ситуации, где следует воспользоваться справочной информацией или другими вспомогательными средствами;
способность переносить полученные в ходе обучения знания в актуальную ситуацию (при решении житейских задач, требующих математических знаний);
способность ориентироваться в требованиях и правилах проведения промежуточной и итоговой аттестации;
овладение основами финансовой грамотности.
Метапредметные результаты
Овладение универсальными учебными познавательными действиями:
устанавливать причинно-следственные связи в ходе усвоения математического материала;
выявлять дефицит данных, необходимых для решения поставленной задачи;
с помощью учителя выбирать способ решения математической задачи (сравнивать возможные варианты решения);
применять и преобразовывать знаки и символы в ходе решения математических задач;
устанавливать искомое и данное при решении математической задачи;
понимать и интерпретировать информацию различных видов и форм представления;
иллюстрировать решаемые задачи графическими схемами;
эффективно запоминать и систематизировать информацию.
понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации.
Овладение универсальными учебными коммуникативными действиями:
организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками в процессе решения задач;
взаимодействовать и находить общие способы работы; работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
прогнозировать возникновение конфликтов при наличии разных точек зрения и разрешать конфликты на основе учёта интересов и позиций всех участников;
аргументировать свою позицию и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности;
выполнять свою часть работы, достигать качественного результата и координировать свои действия с другими членами команды;
оценивать качество своего вклада в общий продукт.
Овладение универсальными учебными регулятивными действиями:
ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
формулировать и удерживать учебную задачу, составлять план и последовательность действий;
осуществлять контроль по образцу и вносить необходимые коррективы;
контролировать процесс и результат учебной математической деятельности;
адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
сличать способ действия и его результат с заданным эталоном с целью обнаружения отклонений и отличий от эталона.
предвидеть трудности, которые могут возникнуть при решении учебной задачи;
понимать причины, по которым не был достигнут требуемый результат деятельности, определять позитивные изменения и направления, требующие дальнейшей работы;
регулировать способ выражения эмоций.
ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ
К концу обучения в 9 классе обучающийся получит следующие предметные результаты:
Числа и вычисления
Сравнивать и упорядочивать рациональные и иррациональные числа.
Выполнять арифметические действия с рациональными числами, сочетая устные и письменные приёмы, выполнять вычисления с иррациональными числами.
Находить значения степеней с целыми показателями и корней; вычислять значения числовых выражений.
Округлять действительные числа, выполнять прикидку результата вычислений, оценку числовых выражений.
Уравнения и неравенства
Решать линейные и квадратные уравнения, уравнения, сводящиеся к ним, простейшие дробно-рациональные уравнения.
Решать простейшие системы двух линейных уравнений с двумя переменными и системы двух уравнений, в которых одно уравнение не является линейным (по визуальной опоре).
Решать простейшие текстовые задачи алгебраическим способом с помощью составления уравнения или системы двух уравнений с двумя переменными.
Проводить простейшие исследования уравнений и систем уравнений, в том числе с применением графических представлений (устанавливать, имеет ли уравнение или система уравнений решения, если имеет, то сколько, и пр.).
Решать линейные неравенства, квадратные неравенства; изображать решение неравенств на числовой прямой, записывать решение с помощью символов.
Решать системы линейных неравенств, системы неравенств, включающие квадратное неравенство; изображать решение системы неравенств на числовой прямой, записывать решение с помощью символов.
Использовать неравенства при решении различных задач.
Функции
Распознавать функции изученных видов. Показывать схематически расположение на координатной плоскости графиков функций вида: y = kx, y = kx + b, , y = ax2 + bx +c, y = x3, y = 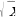 , y =
, y = 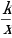 в зависимости от значений коэффициентов; описывать свойства функций.
в зависимости от значений коэффициентов; описывать свойства функций.
Строить и изображать схематически графики квадратичных функций, описывать свойства квадратичных функций по их графикам.
Распознавать квадратичную функцию по формуле, приводить примеры квадратичных функций из реальной жизни, физики, геометрии.
Арифметическая и геометрическая прогрессии
Распознавать арифметическую и геометрическую прогрессии при разных способах задания.
Выполнять вычисления с использованием формул n-го члена арифметической и геометрической прогрессий, суммы первых n членов (c опорой на справочную информацию).
Решать задачи, связанные с числовыми последовательностями, в том числе задачи из реальной жизни (с использованием калькулятора, цифровых технологий).
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
| № п/п
| Наименование разделов и тем программы
| Количество часов | Электронные (цифровые) образовательные ресурсы
|
| Всего
| Контрольные работы
| Практические работы
|
| 1 | Числа и вычисления. Действительные числа | 9 | 1 |
|
|
| 2 | Уравнения и неравенства. Уравнения с одной переменной | 14 | 1 |
|
|
| 3 | Уравнения и неравенства. Системы уравнений | 14 | 1 |
|
|
| 4 | Уравнения и неравенства. Неравенства | 16 | 2 |
|
|
| 5 | Функции | 16 | 1 |
|
|
| 6 | Числовые последовательности | 15 | 2 |
|
|
| 7 | Повторение, обобщение, систематизация знаний | 18 | 1 |
|
|
| ОБЩЕЕ КОЛИЧЕСТВО ЧАСОВ ПО ПРОГРАММЕ | 102 | 9 |
|
|
1Темы, выделенные курсивом, изучаются ознакомительно















