Адаптированная рабочая программа по геометрии для учеников 8 класса

Муниципальное казенное общеобразовательное учреждение

«Южная средняя общеобразовательная школа»

«Рассмотрено» Руководитель ШМО _______________Шаварикова С.Б. Протокол №1 от 28.08.24

«Согласовано» Заместитель директора по УР ______________Манджикова Т.А. 29.08.24

«Утверждено» Директор МКОУ ЮСОШ ______________Найденова Н.И. Приказ №70 от 30.08.24

Адаптированная рабочая программа

по геометрии

ученика 8 класса

Составила учитель математики:

Шаварикова С.Б.

П. Южный

2024г.

Пояснительная записка Рабочая программа составлена на основе:

• положения МКОУ ЮСОШ «О рабочей программе педагога»;

• основной образовательной программы основного общего образования;

• учебного плана МКОУ ЮСОШ на 2024-2025 учебный год;

• учебно-методического комплекса: УМК «Геометрия. 7-9 классы» Л.С. Атанасян, В.Ф. Бутузов и др. (М.: Просвещение, 2023).

Особенности познавательной сферы

У подростков с ОВЗ сохраняются недостаточный уровень сформированности познавательных процессов и пониженная продуктивность интеллектуальной деятельности.

Сохраняются неустойчивость внимания, трудности переключения с одного вида деятельности на другой, повышенные истощаемость, отвлекаемость на посторонние раздражители, что затрудняет последовательное и контролируемое выполнение длинного ряда операций.

Трудности вызывает построение логических рассуждений, опирающихся на установление причинно-следственных связей, на необходимость доказательного обоснования ответа, способность делать вывод на основе анализа полученной информации. Подросток с ОВЗ затрудняется в осуществлении логической операции перехода от видовых признаков к родовому понятию, в обобщении, интегрировании информации из различных источников, в построении простейших прогнозов. Следует отметить, что часто возникают трудности использования мыслительной операции, сформированной на одном учебном материале, в работе с другим материалом или в изменившихся условиях сходных задач.

При выполнении классификации, объединении предметов и явлений в группы по определенным признакам сложности возникают при самостоятельном определении основания для классификации и его вербальном обозначении.

Понятийные формы мышления долгое время не достигают уровня нормального развития, затрудняется процесс абстрагирования, оперирования понятиями, включения понятий в разные системы обобщения. Все это осложняется недостаточной способностью к использованию знаково-символических средств. Школьники с ОВЗ нуждаются в сопровождении изучения программного материала дополнительной визуализацией, конкретизацией, примерами, связью с практическим опытом.

Для обучающихся с подросткового возраста характерна слабость речевой регуляции действий, они испытывают затруднения в речевом оформлении, не могут спланировать свои действия и дать о них вербальный отчет.

Цели и задачи учебного предмета «Геометрия» на уровне основного общего образования

Овладение учащимися системой геометрических знаний и умений необходимо в повседневной жизни, для изучения смежных дисциплин и продолжения образования.

Практическая значимость школьного курса геометрии обусловлена тем, что его объектом являются пространственные формы и количественные отношения действительного мира. Геометрическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.

Геометрия является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь, это относится к предметам естественно- научного цикла, в частности, к физике. Развитие логического мышления учащихся при обучении геометрии способствует усвоению предметов гуманитарного цикла.

Геометрия существенно расширяет кругозор учащихся, знакомя их с индукцией и дедукцией, обобщением и конкретизацией, анализом и синтезом, классификацией и систематизацией, абстрагированием, аналогией. Активное использование задач на всех этапах учебного процесса развивает творческие способности школьников.

При обучении геометрии формируются умения и навыки умственного труда – планирование своей работы, поиск рациональных путей её выполнения, критическая оценка результатов. В процессе обучения геометрии школьники должны научиться излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобрести навыки чёткого, аккуратного и грамотного выполнения математических записей.

Важнейшей задачей школьного курса геометрии является развитие логического мышления учащихся. Сами объекты геометрических умозаключений и принятые в геометрии правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратно и наглядно вскрывают механизм логических построений и учат их применению. Тем самым геометрия занимает ведущее место в формировании научно-теоретического мышления школьников. Раскрывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, способствуя восприятию геометрических форм, усвоению понятия симметрии, геометрия вносит значительный вклад в эстетическое воспитание учащихся. Её изучение развивает воображение школьников, существенно обогащает и развивает их пространственные представления.

В курсе геометрии можно выделить следующие содержательные линии: «Наглядная геометрия», «Геометрические фигуры», «Измерение геометрических величин»,

«Координаты», «Векторы», «Логика и множества», «Геометрия в историческом развитии».

Материал, относящийся к линии «Наглядная геометрия» способствует развитию пространственных представлений учащихся в рамках изучения планиметрии.

Содержание разделов «Геометрические фигуры» и «Измерение геометрических величин» нацелено на получение конкретных знаний о геометрической фигуре как важнейшей математической модели для описания окружающего мира.

Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:

Личностные УУД:

• Осознание этнической принадлежности, знание истории, языка, культуры своего народа, своего края, основ культурного наследия народов России и человечества (идентичность человека с российской многонациональной культурой, сопричастность истории народов и государств, находившихся на территории современной России); интериоризация гуманистических, демократических и традиционных ценностей многонационального российского общества

• Готовность и способность осознанному выбору и построению дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений, с учетом устойчивых познавательных интересов

• Сформированность ответственного отношения к учению; уважительного отношения к труду, наличие опыта участия в социально значимом труде. Осознание значения семьи в жизни человека и общества, принятие ценности семейной жизни, уважительное и заботливое отношение к членам своей семьи.

• Осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению, мировоззрению, культуре, языку, вере, гражданской позиции.

• Освоенность социальных норм, правил поведения, ролей и форм социальной жизни в группах и сообществах. Участие в школьном самоуправлении и общественной жизни в пределах возрастных компетенций с учетом региональных, этнокультурных, социальных и экономических особенностей (формирование готовности к участию в процессе упорядочения социальных связей и отношений, в которые включены и которые формируют сами учащиеся;

• включенность в непосредственное гражданское участие, готовность участвовать в жизнедеятельности подросткового общественного объединения, продуктивно взаимодействующего с социальной средой и социальными институтами;

• Сформированность ценности здорового и безопасного образа жизни; интериоризация правил индивидуального и коллективного безопасного поведения в чрезвычайных ситуациях, угрожающих жизни и здоровью людей, правил поведения на транспорте и на дорогах.

• Развитость эстетического сознания через освоение художественного наследия народов России и мира, творческой деятельности эстетического характера (способность понимать художественные произведения, отражающие разные этнокультурные

Метапредметные:

Регулятивные УУД:

Умение самостоятельно определять цели обучения, ставить и формулировать новые задачи в учебе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности. Обучающийся сможет:

• формулировать учебные задачи как шаги достижения поставленной цели деятельности;

• обосновывать целевые ориентиры и приоритеты ссылками на ценности, указывая и обосновывая логическую последовательность шагов.

Умение самостоятельно планировать пути достижения целей, в том числе альтернативные, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Обучающийся сможет:

• составлять план решения проблемы (выполнения проекта, проведения исследования);

• определять потенциальные затруднения при решении учебной и познавательной задачи и находить средства для их устранения;

• описывать свой опыт, оформляя его для передачи другим людям в виде технологии решения практических задач определенного класса;

• планировать и корректировать свою индивидуальную образовательную траекторию.

Умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией. Обучающийся сможет:

• систематизировать (в том числе выбирать приоритетные) критерии планируемых результатов и оценки своей деятельности;

• отбирать инструменты для оценивания своей деятельности, осуществлять самоконтроль своей деятельности в рамках предложенных условий и требований;

• находить достаточные средства для выполнения учебных действий в изменяющейся ситуации и/или при отсутствии планируемого результата;

• работая по своему плану, вносить коррективы в текущую деятельность на основе анализа изменений ситуации для получения запланированных характеристик продукта/результата;

• устанавливать связь между полученными характеристиками продукта и характеристиками процесса деятельности и по завершении деятельности предлагать изменение характеристик процесса для получения улучшенных характеристик продукта.

Умение оценивать правильность выполнения учебной задачи, собственные возможности ее решения. Обучающийся сможет:

• анализировать и обосновывать применение соответствующего инструментария для выполнения учебной задачи;

• свободно пользоваться выработанными критериями оценки и самооценки, исходя из цели и имеющихся средств, различая результат и способы действий;

• оценивать продукт своей деятельности по заданным и/или самостоятельно определенным критериям в соответствии с целью деятельности;

• обосновывать достижимость цели выбранным способом на основе оценки своих внутренних ресурсов и доступных внешних ресурсов.

Владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной. Обучающийся сможет:

• наблюдать и анализировать собственную учебную и познавательную деятельность и деятельность других обучающихся в процессе взаимопроверки;

• соотносить реальные и планируемые результаты индивидуальной образовательной деятельности и делать выводы;

• ретроспективно определять, какие действия по решению учебной задачи или параметры этих действий привели к получению имеющегося продукта учебной деятельности.

Познавательные УУД:

Умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное, по аналогии) и делать выводы. Обучающийся сможет:

• определять обстоятельства, которые предшествовали возникновению связи между явлениями, из этих обстоятельств выделять определяющие, способные быть причиной данного явления, выявлять причины и следствия явлений;

• строить рассуждение от общих закономерностей к частным явлениям и от частных явлений к общим закономерностям;

• строить рассуждение на основе сравнения предметов и явлений, выделяя при этом общие признаки;

• самостоятельно указывать на информацию, нуждающуюся в проверке, предлагать и применять способ проверки достоверности информации.

Умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач. Обучающийся сможет:

• строить модель/схему на основе условий задачи и/или способа ее решения;

• создавать вербальные, вещественные и информационные модели с выделением существенных характеристик объекта для определения способа решения задачи в соответствии с ситуацией.

• преобразовывать модели с целью выявления общих законов, определяющих данную предметную область.

Смысловое чтение. Обучающийся сможет:

• устанавливать взаимосвязь описанных в тексте событий, явлений, процессов;

• резюмировать главную идею текста;

• преобразовывать текст, «переводя» его в другую модальность, интерпретировать текст (художественный и нехудожественный – учебный, научно-популярный, информационный, текст non-fiction).

Формирование и развитие экологического мышления, умение применять его в познавательной, коммуникативной, социальной практике и профессиональной ориентации. Обучающийся сможет:

• распространять экологические знания и участвовать в практических делах по защите окружающей среды;

• выражать свое отношение к природе через рисунки, сочинения, модели, проектные работы.

Развитие мотивации к овладению культурой активного использования словарей и других поисковых систем. Обучающийся сможет:

• формировать множественную выборку из поисковых источников для объективизации результатов поиска.

Коммуникативные УУД:

Умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; формулировать, аргументировать и отстаивать свое мнение. Обучающийся сможет:

• определять свои действия и действия партнера, которые способствовали или препятствовали продуктивной коммуникации;

• корректно и аргументированно отстаивать свою точку зрения, в дискуссии уметь выдвигать контраргументы, перефразировать свою мысль (владение механизмом эквивалентных замен);

• критически относиться к собственному мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;

• предлагать альтернативное решение в конфликтной ситуации;

• выделять общую точку зрения в дискуссии;

• договариваться о правилах и вопросах для обсуждения в соответствии с поставленной перед группой задачей;

• организовывать учебное взаимодействие в группе (определять общие цели, распределять роли, договариваться друг с другом и т. д.);

• устранять в рамках диалога разрывы в коммуникации, обусловленные непониманием/неприятием со стороны собеседника задачи, формы или содержания диалога.

Умение осознанно использовать речевые средства в соответствии с задачей коммуникации для выражения своих чувств, мыслей и потребностей для планирования и регуляции своей деятельности; владение устной и письменной речью, монологической контекстной речью. Обучающийся сможет:

• соблюдать нормы публичной речи, регламент в монологе и дискуссии в соответствии с коммуникативной задачей;

• высказывать и обосновывать мнение (суждение) и за-прашивать мнение партнера в рамках диалога;

• создавать письменные «клишированные» и оригинальные тексты с использованием необходимых речевых средств;

• использовать вербальные средства (средства логической связи) для выделения смысловых блоков своего выступления.

Формирование и развитие компетентности в области использования информационно- коммуникационных технологий (далее – ИКТ). Обучающийся сможет:

• целенаправленно искать и использовать информационные ресурсы, необходимые для решения учебных и практических задач с помощью средств ИКТ;

• выбирать, строить и использовать адекватную информационную модель для передачи своих мыслей средствами естественных и формальных языков в соответствии с условиями коммуникации;

• использовать информацию с учетом этических и правовых норм;

• создавать информационные ресурсы разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности.

• использовать компьютерные технологии (включая выбор адекватных задаче инструментальных программно-аппаратных средств и сервисов) для решения

информационных и коммуникационных учебных задач, в том числе: вычисление, написание писем, сочинений, докладов, рефератов, создание презентаций и др.

В результате изучения учебного предмета «Геометрия» на уровне освоения основного общего образования Обучающийся 8 класса научится (для использования в повседневной жизни и обеспечения возможности успешного продолжения образования на базовом уровне):

Элементы теории множеств и математической логики

• оперировать на базовом уровне понятиями: определение, аксиома, теорема, доказательство;

• приводить примеры и контрпримеры для подтверждения своих высказываний.

Геометрические фигуры

• оперировать на базовом уровне понятиями геометрических фигур;

• извлекать информацию о геометрических фигурах, представленную на чертежах в явном виде;

• применять для решения задач геометрические факты, если условия их применения заданы в явной форме;

• решать задачи на нахождение геометрических величин по образцам или алгоритмам.

В повседневной жизни и при изучении других предметов:

• использовать свойства геометрических фигур для решения типовых задач, возникающих в ситуациях повседневной жизни, задач практического содержания.

Измерения и вычисления

• применять формулы площади, когда все данные имеются в условии;

• применять теорему Пифагора для вычисления длин, расстояний, площадей в простейших случаях.

В повседневной жизни и при изучении других предметов:

• вычислять расстояния на местности в стандартных ситуациях, площади в простейших случаях, применять формулы в простейших ситуациях в повседневной жизни.

Геометрические построения

• изображать типовые плоские фигуры и фигуры в пространстве от руки и с помощью инструментов.

В повседневной жизни и при изучении других предметов:

• выполнять простейшие построения на местности, необходимые в реальной жизни.

Геометрические преобразования

• строить фигуру, симметричную данной фигуре относительно оси и точки.

В повседневной жизни и при изучении других предметов:

• распознавать симметричные фигуры в окружающем мире.

История математики

• описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;

• знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;

• понимать роль математики в развитии России.

Методы математики

• выбирать подходящий изученный метод для решения изученных типов математических задач;

• приводить примеры математических закономерностей в окружающей действительности и произведениях искусства.

Обучающийся 8 класса получит возможность научиться для обеспечения возможности успешного продолжения образования на базовом и углубленном уровнях:

Элементы теории множеств и математической логики

• оперировать понятиями: определение, теорема, аксиома.

Геометрические фигуры

• оперировать понятиями геометрических фигур;

• извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;

• применять геометрические факты для решения задач, в том числе, предполагающих несколько шагов решения;

• формулировать в простейших случаях свойства и признаки фигур;

• доказывать геометрические утверждения;

• владеть стандартной классификацией плоских фигур (треугольников).

В повседневной жизни и при изучении других предметов:

• использовать свойства геометрических фигур для решения задач практического характера и задач из смежных дисциплин.

Отношения

• оперировать понятиями: подобие фигур, подобные фигуры, подобные треугольники;

• применять теорему Фалеса и теорему о пропорциональных отрезках при решении задач;

• характеризовать взаимное расположение прямой и окружности, двух окружностей.

В повседневной жизни и при изучении других предметов:

• использовать отношения для решения задач, возникающих в реальной жизни.

Измерения и вычисления

• оперировать представлениями о площади как величине. Применять теорему Пифагора, формулы площади, при решении многошаговых задач, в которых не все данные представлены явно, а требуют вычислений, оперировать более широким количеством формул длины, площади, вычислять характеристики комбинаций фигур (окружностей и многоугольников), вычислять расстояния между фигурами;

• формулировать задачи на вычисление длин и площадей и решать их.

В повседневной жизни и при изучении других предметов:

• проводить вычисления на местности;

• применять формулы при вычислениях в смежных учебных предметах, в окружающей действительности.

Геометрические построения

• изображать геометрические фигуры по текстовому и символьному описанию;

• свободно оперировать чертежными инструментами в несложных случаях,

• выполнять построения треугольников, применять отдельные методы построений циркулем и линейкой и проводить простейшие исследования числа решений;

• изображать типовые плоские фигуры и объемные тела с помощью простейших компьютерных инструментов.

В повседневной жизни и при изучении других предметов:

• выполнять простейшие построения на местности, необходимые в реальной жизни;

• оценивать размеры реальных объектов окружающего мира.

Преобразования

• строить фигуру, подобную данной, пользоваться свойствами подобия для обоснования свойств фигур.

В повседневной жизни и при изучении других предметов:

• применять подобие для построений и вычислений.

История математики

• характеризовать вклад выдающихся математиков в развитие математики и иных научных областей;

• понимать роль математики в развитии России.

Методы математики

• используя изученные методы, проводить доказательство, выполнять опровержение;

• выбирать изученные методы и их комбинации для решения математических задач;

• использовать математические знания для описания закономерностей в окружающей действительности и произведениях искусства;

• применять простейшие программные средства и электронно- коммуникационные системы при решении математических задач.

Содержание учебного предмета «Геометрия» 8 класса Геометрические фигуры

Фигуры в геометрии и в окружающем мире

Геометрическая фигура. Формирование представлений о метапредметном понятии

«фигура».

Точка, линия, отрезок, прямая, луч, ломаная, плоскость, угол, биссектриса угла и ее свойства, виды углов, многоугольники, круг.

Осевая симметрия геометрических фигур. Центральная симметрия геометрических фигур.

Многоугольники

Многоугольник, его элементы и его свойства. Распознавание некоторых многоугольников. Выпуклые и невыпуклые многоугольники. Правильные многоугольники.

Четырехугольники. Параллелограмм, ромб, прямоугольник, квадрат, трапеция, равнобедренная трапеция. Свойства и признаки параллелограмма, ромба, прямоугольника, квадрата.

Окружность, круг

Окружность, круг, их элементы и свойства; центральные и вписанные углы. Касательная и секущая к окружности, их свойства. Вписанные и описанные окружности для треугольников, четырехугольников, правильных многоугольников.

Отношения Подобие

Пропорциональные отрезки, подобие фигур. Подобные треугольники. Признаки подобия.

Взаимное расположение прямой и окружности, двух окружностей.

Измерения и вычисления Величины

Понятие о площади плоской фигуры и ее свойствах. Измерение площадей.

Единицы измерения площади.

Измерения и вычисления

Инструменты для измерений и построений; измерение и вычисление углов, длин (расстояний), площадей. Тригонометрические функции острого угла в прямоугольном треугольнике. Тригонометрические функции тупого угла. Вычисление элементов треугольников с использованием тригонометрических соотношений. Сравнение и вычисление площадей. Теорема Пифагора.

Расстояния

Расстояние между точками. Расстояние от точки до прямой. Расстояние между фигурами.

Геометрические построения

Геометрические построения для иллюстрации свойств геометрических фигур.

Инструменты для построений: циркуль, линейка, угольник. Простейшие построения циркулем и линейкой: построение биссектрисы угла, перпендикуляра к прямой, угла, равного данному.

Построение треугольников по трем сторонам, двум сторонам и углу между ними, стороне и двум прилежащим к ней углам.

Деление отрезка в данном отношении.

Геометрические преобразования Преобразования

Понятие преобразования. Представление о метапредметном понятии

«преобразование». Подобие.

Движения

Осевая и центральная симметрия.

История математики

Возникновение математики как науки, этапы ее развития. Основные разделы математики. Выдающиеся математики и их вклад в развитие науки.

От земледелия к геометрии. Пифагор и его школа. Фалес, Архимед. Платон и Аристотель. История числа π. Золотое сечение. «Начала» Евклида. Л Эйлер, Н.И.Лобачевский. История пятого постулата.

Геометрия и искусство. Геометрические закономерности окружающего мира.

Астрономия и геометрия. Что и как узнали Анаксагор, Эратосфен и Аристарх о размерах Луны, Земли и Солнца. Расстояния от Земли до Луны и Солнца. Измерение расстояния от Земли до Марса.

Роль российских ученых в развитии математики: Н.И. Лобачевский.

Математика в развитии России: Петр I, школа математических и навигацких наук, развитие российского флота, А.Н. Крылов. Космическая программа и М.В. Келдыш.

Содержание учебного предмета «Геометрия» 8 класса Геометрические фигуры

Фигуры в геометрии и в окружающем мире

Геометрическая фигура. Формирование представлений о метапредметном понятии

«фигура».

Точка, линия, отрезок, прямая, луч, ломаная, плоскость, угол, биссектриса угла и ее свойства, виды углов, многоугольники, круг.

Осевая симметрия геометрических фигур. Центральная симметрия геометрических фигур.

Многоугольники

Многоугольник, его элементы и его свойства. Распознавание некоторых многоугольников. Выпуклые и невыпуклые многоугольники. Правильные многоугольники.

Четырехугольники. Параллелограмм, ромб, прямоугольник, квадрат, трапеция, равнобедренная трапеция. Свойства и признаки параллелограмма, ромба, прямоугольника, квадрата.

Окружность, круг

Окружность, круг, их элементы и свойства; центральные и вписанные углы. Касательная и секущая к окружности, их свойства. Вписанные и описанные окружности для треугольников, четырехугольников, правильных многоугольников.

Отношения Подобие

Пропорциональные отрезки, подобие фигур. Подобные треугольники. Признаки подобия.

Взаимное расположение прямой и окружности, двух окружностей.

Измерения и вычисления Величины

Понятие о площади плоской фигуры и ее свойствах. Измерение площадей.

Единицы измерения площади.

Измерения и вычисления

Инструменты для измерений и построений; измерение и вычисление углов, длин (расстояний), площадей. Тригонометрические функции острого угла в прямоугольном треугольнике. Тригонометрические функции тупого угла. Вычисление элементов треугольников с использованием тригонометрических соотношений. Сравнение и вычисление площадей. Теорема Пифагора.

Расстояния

Расстояние между точками. Расстояние от точки до прямой. Расстояние между фигурами.

Геометрические построения

Геометрические построения для иллюстрации свойств геометрических фигур.

Инструменты для построений: циркуль, линейка, угольник. Простейшие построения циркулем и линейкой: построение биссектрисы угла, перпендикуляра к прямой, угла, равного данному.

Построение треугольников по трем сторонам, двум сторонам и углу между ними, стороне и двум прилежащим к ней углам.

Деление отрезка в данном отношении.

Геометрические преобразования Преобразования

Понятие преобразования. Представление о метапредметном понятии

«преобразование». Подобие.

Движения

Осевая и центральная симметрия.

История математики

Возникновение математики как науки, этапы ее развития. Основные разделы математики. Выдающиеся математики и их вклад в развитие науки.

От земледелия к геометрии. Пифагор и его школа. Фалес, Архимед. Платон и Аристотель. История числа π. Золотое сечение. «Начала» Евклида. Л Эйлер, Н.И.Лобачевский. История пятого постулата.

Геометрия и искусство. Геометрические закономерности окружающего мира.

Астрономия и геометрия. Что и как узнали Анаксагор, Эратосфен и Аристарх о размерах Луны, Земли и Солнца. Расстояния от Земли до Луны и Солнца. Измерение расстояния от Земли до Марса.

Роль российских ученых в развитии математики: Н.И. Лобачевский.

Математика в развитии России: Петр I, школа математических и навигацких наук, развитие российского флота, А.Н. Крылов. Космическая программа и М.В. Келдыш.

Класс 8

Тематическое планирование по геометрии

Количество часов по учебному плану: всего 68 часов; в неделю 2 часа. Контрольных работ 5.

Учебник: «Геометрия. 7-9 классы» Л.С. Атанасян, В.Ф. Бутузов. – М.: Просвещение, 2017

Раздел	№ урока	Название темы урока	Характеристика основных видов деятельности (на уровне учебных действий)
I. Четырехуголь ники (14 часов)	1	Многоугольники	Объяснять, что такое ломаная, многоугольник, его вершины, смежные стороны, диагонали, изображать и распознавать многоугольники на чертежах; показывать элементы многоугольника, его внутрненнюю и внешнюю области; изображать и распознвать выпуклые и невыпуклые многоугольники; формулировать и доказывать утверждения о сумме углов выпуклого многоугольника и сумме его внешних углов; обяъснять, какие стороны (вершины) четырехугольника называются противоположными; формулировать определения параллелограмма, трапеции, равнобедренной и прямоугольной трапеций, прямоугольника, ромба, квадрата; изображать и распознавать эти четырехугольники; формулировать и доказывать утверждения об их свойствах и признаках; решать задачи на вычисление, доказательство и построение, связанные с этими видами четырёхугольников; объяснять, какие две точки называются симметричными относительно прямой (точки), в каком случае фигура называется симметричной относительно прямой (точки) и что такое ось (центр) симметрии фигуры; приводить примеры фигур, обладающих осевой (центральной) симметрией, а также примеры осевой и центральной симметрий в окружающей нас обстановке.
	2	Решение задач по теме «Многоугольники»
	3	Параллелограмм
	4	Признаки параллелограмма
	5	Решение задач по теме «Параллелограмм»
	6	Трапеция
	7	Решение задач по теме «Трапеция»
	8	Решение задач по теме «Трапеция»
	9	Прямоугольник
	10	Ромб. Квадрат
	11	Осевая и центральная симметрии
	12	Решение задач по теме «Четырёхугольники»
	13	Обобщающий урок по теме «Четырехугольники»
	14	Контрольная работа №1 по теме «Четырехугольники»
II. Площадь (16 часов)	15	Анализ контрольной работы. Площадь многоугольника	Объяснять, как производится измерение площадей

	16	Площадь прямоугольника	многоугольников, какие многоугольники называются равновеликими и какие равносоставленными; формулировать основные свойства площадей и выводить с их помощью формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; формулировать и доказывать теорему об отношении площадей треугольников, имеющих по равному углу; формулировать и доказывать теорему Пифагора и обратную ей; выводить формулу Герона для площади треугольника; решать задачи на вычисление и доказательство, связанные с формулами площадей и теоремой Пифагора.
	17	Площадь параллелограмма
	18	Площадь параллелограмма
	19	Площадь треугольника
	20	Площадь треугольника
	21	Площадь трапеции
	22	Площадь трапеции
	23	Теорема Пифагора
	24	Теорема Пифагора
	25	Теорема Пифагора
	26	Решение задач по теме «Площадь. Теорема Пифагора»
	27	Обобщающий урок по теме «Площадь»
	28	Контрольная работа №2 по теме «Площадь»
III. Подобные треугольники (19 часов)	29	Анализ контрольной работы. Определение подобных треугольников	Объяснять понятие пропорциональности отрезков; формулировать определения подобных треугольников и коэффициента подобия; формулировать и доказывать теоремы: об отношении площадей подобных треугольников, о признаках подобия треугольников, о средней линии треугольника, о пересечении медиан треугольника, о пропорциональных отрезках в прямоугольном треугольнике; объяснять, как можно использовать свойства подобных треугольников в измерительных работах на местности; объяснять, как ввести понятие подобия для произвольных фигур; формулировать определение и иллюстрировать понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника; выводить основное тригонометрическое тождество и значения синуса, косинуса и тангенса для углов 30о, 45о, 60о; решать задачи, связанные с подобием треугольников, для вычисления значений тригонометрических функций использовать компьютерные программы.
	30	Отношение площадей подобных треугольников
	31	Первый признак подобия треугольников
	32	Первый признак подобия треугольников
	33	Второй и третий признаки подобия треугольников
	34	Второй и третий признаки подобия треугольников
	35	Решение задач по теме «Подобные треугольники»
	36	Контрольная работа №3 по теме «Подобные треугольники»
	37	Анализ контрольной работы. Средняя линия треугольника
	38	Свойство медиан треугольника
	39	Пропорциональные отрезки в прямоугольном треугольнике
	40	Пропорциональные отрезки в прямоугольном треугольнике
	41	Измерительные работы на местности
	42	Задачи на построение методом подобных треугольников
	43	Синус, косинус и тангенс острого угла прямоугольного треугольника

	44	Значение синуса, косинуса и тангенса для углов 300, 450, 600
	45	Соотношение между сторонами и углами прямоугольного треугольника
	46	Решение задач по теме «Соотношение между сторонами и углами прямоугольного треугольника»
	47	Контрольная работа №4 по теме «Соотношения между сторонами и углами прямоугольного треугольника»
IV. Окружность (17 часов)	48	Анализ контрольной работы. Взаимное расположение прямой и окружности	Исследовать взаимное расположение прямой и окружности; формулировать определение касательной к окружности; формулировать и доказывать теоремы: о свойстве касательной, о признаке касательной, об отрезках касательных, проведенных из одной точки; формулировать понятие центрального угла и градусной меры дуги окружности; формулировать и доказывать теоремы: о вписанном угле, о произведении отрезков пересекающихся хорд; формулировать и доказывать теоремы, связанные с замечательными точками треугольника: о биссектрисе угла и, как следствие, о пересечении биссектрис треугольника; о серединном перпендикуляре к отрезку и, как следствие, о пересечении серединных перпендикуляров к сторонам треугольника; о пересечении высот треугольника; формулировать определения окружностей, вписанной в многоугольник и описанной около многоугольника; формулировать и доказывать теоремы: об окружности, вписанной в треугольника; об окружности, описанной около треугольника; о свойстве сторон описанного четырехугольника; о свойстве углов вписанного четырехугольника; решать задачи на вычисление, доказательство и построение, связанные с окружностью, вписанными и описанными треугольниками и четырехугольниками; исследовать
	49	Касательная к окружности
	50	Касательная к окружности
	51	Градусная мера дуги окружности
	52	Теорема о вписанном угле
	53	Теорема об отрезках пересекающихся хорд
	54	Решение задач по теме «Центральные и вписанные углы»
	55	Свойство биссектрисы угла
	56	Серединный перпендикуляр
	57	Теорема о пересечении высот треугольника
	58	Вписанная окружность
	59	Свойство описанного четырехугольника
	60	Описанная окружность
	61	Свойство вписанного четырехугольника
	62	Решение задач по теме «Окружность»
	63	Решение задач по теме «Окружность»
	64	Контрольная работа №5 по теме «Окружность»

			свойства конфигураций, связанных с окружностью, с помощью компьютерных программ.
V. Итоговое повторение (4 часа)	65	Решение задач по теме «Четырехугольники»
	66	Решение задач по теме «Площадь»
	67	Решение задач по теме «Подобные треугольники»
	68	Решение задач по теме «Окружность»

Критерии и нормы оценочной деятельности

Оценивание письменных контрольных работ:

Каждая контрольная работа рассчитана на один урок. Все работы составлены в четырех вариантах одинакового уровня сложности.

Для подготовки к контрольной работе даются задания, проверяющие те же знания и умения, что и задания контрольной работы.

Каждая работа состоит из трех частей, соответствующих форме предлагаемых заданий.

В часть А включаются задания с выбором ответа. Учащимися нужно выбрать из предложенных вариантов либо верное утверждение, либо нужный рисунок. При этом верных ответов может быть несколько. Задание считается выполненным верно, если указаны номера всех верных ответов.

В часть В входят вычислительные задачи, которые необходимо решить и записать в тетради число, которое получилось в результате вычислений.

В части С имеются и задачи на доказательство, и задачи на вычисление геометрических величин. При решение этих задач необходимо приводить обоснования с использованием геометрических фактов. Последняя задача, в каждом варианте предназначена для наиболее подготовленных учащихся.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

• работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

Оценка устных ответов:

Устный опрос является одним из основных способов учета знаний учащихся. Развернутый ответ ученика должен представлять собой связное, логически последовательное сообщение на

определенную тему, показывать его умение применять определения, правила в конкретных случаях.

При оценке ответа ученика надо руководствоваться следующими критериями:

1. полнота и правильность ответа;

2. степень осознанности, понимания изученного;

3. языковое оформление ответа.

Ответ оценивается отметкой «5», если ученик:

1. полно излагает изученный материал, дает правильное определение языковых понятий;

2. обнаруживает понимание материала, может обосновать свои суждения, применить знания на практике, привести необходимые примеры не только по учебнику, но и самостоятельно составленные;

3. излагает материал последовательно и правильно с точки зрения норм литературного языка.

Ответ оценивается отметкой «4», если ученик:

Ученик дает ответ, удовлетворяющий тем же требованиям, что и для оценки «5», но допускает 1-

2 ошибки, которые сам же исправляет, и 1-2 недочета в последовательности и языковом оформлении излагаемого.

Ответ оценивается отметкой «3», если ученик:

Ученик обнаруживает знание и понимание основных положений данной темы, но:

1. излагает материал неполно и допускает неточности в определении понятий или формулировке правил;

2. не умеет достаточно глубоко и доказательно обосновать свои суждения и привести свои примеры;

3. излагает материал непоследовательно и допускает ошибки в языковом оформлении излагаемого.

Ответ оценивается отметкой «2», если ученик:

Ученик обнаруживает незнание большей части соответствующего раздела изучаемого материала, допускает ошибки в формулировке определений и правил, искажающие их смысл, беспорядочно и неуверенно излагает материал. Оценка «2» отмечает такие недостатки в подготовке ученика, которые являются серьезным препятствием к успешному овладению последующим материалом. Ответ оценивается отметкой «1», если ученик:

Ученик обнаруживает полное незнание или непонимание материала.

Отметка («5», «4», «3») может ставиться не только за единовременный ответ, но также и за сумму ответов, данных учеником на протяжении урока (выводится поурочный балл).

Критерии выставления отметок за проверочные тесты:

Отметка «5» ставится, если выполнено 80 – 100 % всех заданий Отметка «4» ставится, если выполнено 60 - 80 % всех заданий Отметка «3» ставится, если выполнено 30 – 60 % всех заданий Отметка «2» ставится, если выполнено менее 30% всех заданий

Контрольная работа №1 по теме «Четырёхугольники» Вариант 1

1. Диагонали прямоугольника 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, ∠𝐴𝐵𝑂 = 36°. Найдите угол 𝐴𝑂𝐷.

2. Найдите углы прямоугольной трапеции, если один из ее углов равен 20°.

3. Стороны параллелограмма относятся как 1 ∶ 2, а его периметр равен 30 см. Найдите стороны параллелограмма.

4. В равнобедренной трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции.

5. Высота 𝐵𝑀, проведенная из вершины угла ромба 𝐴𝐵𝐶𝐷 образует со стороной 𝐴𝐵 угол 30°,

𝐴𝑀 = 4 см. Найдите длину диагонали 𝐵𝐷 ромба, если точка 𝑀 лежит на стороне 𝐴𝐷.

Контрольная работа №1 по теме «Четырёхугольники» Вариант 2

1. Диагонали прямоугольника 𝑀𝑁𝑃𝐾 пересекаются в точке 𝑂, ∠𝑀𝑂𝑁 = 64°. Найдите угол 𝑂𝑀𝑃.

2. Найдите углы равнобедренной трапеции, если один из ее углов на 30° больше второго.

3. Стороны параллелограмма относятся как 3 ∶ 1, а его периметр равен 40 см. Найдите стороны параллелограмма.

4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 48°. Найдите углы трапеции.

5. Высота 𝐵𝑀, проведенная из вершины угла ромба 𝐴𝐵𝐶𝐷 образует со стороной 𝐴𝐵 угол 30°, длина диагонали 𝐴𝐶 равна 6 см. Найдите 𝐴𝑀, если точка 𝑀 лежит на продолжении стороны

𝐴𝐷.

Контрольная работа №2 по теме «Площадь» Вариант 1

1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.

2. Катеты прямоугольного треугольника равна 6 см и 8 см. Найдите гипотенузу и площадь треугольника.

3. 
   Найдите площадь и периметр ромба, если его диагонали равны 8 см и 10 см.

4. ^{В прямоугольной трапеции 𝐴𝐵𝐶𝐾 большая боковая сторона равна 3}√^{2 см, угол 𝐾 равен 45°, а} высота 𝐶𝐻 делит основание 𝐴𝐾 пополам. Найдите площадь трапеции.

Контрольная работа №2 по теме «Площадь» Вариант 2

1. Высота треугольника равна 12 см, а сторона, проведенная к ней, в три раза меньше высоты. Найдите площадь треугольника.

2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катету и гипотенузу треугольника.

3. Диагонали ромба равны 10 см и 12 см. Найдите его площадь и периметр.

4. В прямоугольной трапеции 𝐴𝐵𝐶𝐷 большая боковая сторона равна 8 см см, угол 𝐴 равен 60°, а высота 𝐵𝐻 делит основание 𝐴𝐷 пополам. Найдите площадь трапеции.

Контрольная работа №3 по теме «Подобные треугольники» Вариант 1

1. На рисунке ∠𝐴 = ∠𝐵, 𝐶𝑂 = 4, 𝐷𝑂 = 6, 𝐴𝑂 = 5.

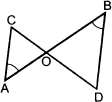
Найдите: а) 𝑂𝐵; б) 𝐴𝐶 ∶ 𝐵𝐷; в) 𝑆_𝐴𝑂𝐶 ∶ 𝑆_𝐵𝑂𝐷.

1. В треугольнике 𝐴𝐵𝐶 𝐴𝐵 = 4 см, 𝐵𝐶 = 7 см, 𝐴𝐶 = 6 см, а в треугольнике 𝑀𝑁𝐾 𝑀𝐾 = 8 см,

𝑀𝑁 = 12 см, 𝐾𝑁 = 14 см. Найдите углы треугольника 𝑀𝑁𝐾, если ∠𝐴 = 80°, ∠𝐵 = 60°.

1. Прямая пересекает стороны треугольника 𝐴𝐵𝐶 в точках 𝑀 и 𝐾 соответственно так, что 𝑀𝐾 ∥

𝐴𝐶, 𝐵𝑀 ∶ 𝐴𝑀 = 1 ∶ 4. Найдите периметр треугольника 𝐵𝑀𝐾, если периметр треугольника 𝐴𝐵𝐶

равен 25 см.

1. В трапеции 𝐴𝐵𝐶𝐷 (𝐴𝐷 и 𝐵𝐶 основания) диагонали пересекаются в точке 𝑂, 𝐴𝐷 = 12 см, 𝐵𝐶 = 4 см. Найдите площадь треугольника 𝐵𝑂𝐶, если площадь треугольника 𝐴𝑂𝐷 равна 45 см².

Контрольная работа №3 по теме «Подобные треугольники» Вариант 2

1. На рисунке 𝑃𝐸 ∥ 𝑁𝐾, 𝑀𝑃 = 8, 𝑀𝑁 = 12, 𝑀𝐸 = 6.

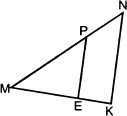
Найдите: а) 𝑀𝐾; б) 𝑃𝐸 ∶ 𝑁𝐾; в) 𝑆_𝑀𝐸𝑃 ∶ 𝑆_𝑀𝐾𝑁.

1. В треугольнике 𝐴𝐵𝐶 𝐴𝐵 = 12 см, 𝐵𝐶 = 18 см, ∠𝐵 = 70°, а в треугольнике 𝑀𝑁𝐾 𝑀𝑁 = 6 см,

𝑁𝐾 = 9 см, ∠𝑁 = 70°. Найдите сторону 𝐴𝐶 и угол 𝐶 треугольника 𝐴𝐵𝐶, если ∠𝐾 = 60°,

𝑀𝐾 = 7 см.

1. Отрезки 𝐴𝐵 и 𝐶𝐷 пересекаются в точке 𝑂 так, что ∠𝐴𝐶𝑂 = ∠𝐵𝐷𝑂, 𝐴𝑂 ∶ 𝑂𝐵 = 2 ∶ 3. Найдите периметр треугольника 𝐴𝐶𝑂, если периметр треугольника 𝐵𝑂𝐷 равен 21 см.

2. В трапеции 𝐴𝐵𝐶𝐷 (𝐴𝐷 и 𝐵𝐶 основания) диагонали пересекаются в точке 𝑂, 𝑆_𝐴𝑂𝐷 = 32 см²,

𝑆_𝐵𝑂𝐶 = 8 см². Найдите меньшее основание трапеции, если большее из них равно 10 см.

Контрольная работа №4 по теме «Соотношение между сторонами и углами треугольника» Вариант 1

1. Средние линии треугольника относятся как 2 ∶ 2 ∶ 4, а периметр треугольника равен 45 см. Найдите стороны треугольника.

2. 
   Медианы треугольника 𝐴𝐵𝐶 пересекаются в точке 𝑂. Через точку 𝑂 проведена прямая, параллельная стороне 𝐴𝐶 и пересекающая стороны 𝐴𝐵 и 𝐵𝐶 в точках 𝐸 и 𝐹 соответственно. Найдите 𝐸𝐹, если сторона 𝐴𝐶 равна 15 см.

3. ^{В прямоугольном треугольнике 𝐴𝐵𝐶 (∠𝐶 = 90°) 𝐴𝐶 = 5 см, 𝐵𝐶 = 5}√^{3 см. Найдите угол 𝐵 и} гипотенузу 𝐴𝐵.

4. В треугольнике 𝐴𝐵𝐶 ∠𝐴 = 𝛼, ∠𝐶 = 𝛽, сторона 𝐵𝐶 = 7 см, 𝐵𝐻 – высота. Найдите 𝐴𝐻.

5. В трапеции 𝐴𝐵𝐶𝐷 продолжения боковых сторон пересекаются в точке 𝐾, причем точка 𝐵 – середина отрезка 𝐴𝐾. Найдите сумму оснований трапеции, если 𝐴𝐷 = 12 см.

Контрольная работа №4 по теме «Соотношение между сторонами и углами треугольника» Вариант 2

1. Стороны треугольника относятся как 4 ∶ 5 ∶ 6, а периметр треугольника, образованного его средними линиями равен 30 см. Найдите средние линии треугольника.

2. Медианы треугольника 𝑀𝑁𝐾 пересекаются в точке 𝑂. Через точку 𝑂 проведена прямая, параллельная стороне 𝑀K и пересекающая стороны 𝑀𝑁 и 𝑁𝐾 в точках 𝐴 и 𝐵 соответственно. Найдите 𝑀𝐾, если сторона 𝐴𝐵 равна 12 см.

1. ^{В прямоугольном треугольнике 𝑃𝐾𝑇 (∠𝑇 = 90°) 𝐾𝑇 = 7 см, 𝑃𝑇 = 7}√^{3 см. Найдите угол 𝐾 и} гипотенузу 𝐾𝑃.

2. В треугольнике 𝐴𝐵𝐶 ∠𝐴 = 𝛼, ∠𝐶 = 𝛽, высота 𝐵𝐻 = 4 см. Найдите 𝐴𝐶.

3. В трапеции 𝑀𝑁𝐾𝑃 продолжения боковых сторон пересекаются в точке 𝐸, причем 𝐸𝐾 = 𝐾𝑃. Найдите разность оснований трапеции, если 𝑁𝐾 = 7 см.

Контрольная работа №5 по теме «Окружность» Вариант 1

1. 𝐴𝐵 и 𝐴𝐶 – отрезки касательных, проведенных к окружности радиуса 9 см. Найдите длины отрезков 𝐴𝐶 и 𝐴𝑂, если 𝐴𝐵 = 12 см.

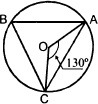2. На рисунке ∪ 𝐴𝐵 ∶ ∪ 𝐵𝐶 = 11 ∶ 12.

Найдите ∠𝐵𝐶𝐴, ∠𝐵𝐴𝐶.

1. Хорды 𝑀𝑁 и 𝑃𝐾 пересекаются в точке 𝐸 так, что 𝑀𝐸 = 12 см, 𝑁𝐸 = 3 см, 𝑃𝐸 = 𝐾𝐸. Найдите

𝑃𝐾.

1. Окружность с центром 𝑂 и радиусом 16 см описана около треугольника 𝐴𝐵𝐶 так, что ∠𝑂𝐴𝐵 = 30°, ∠𝑂𝐶𝐵 = 45°. Найдите стороны 𝐴𝐵 и 𝐵𝐶 треугольника.

Контрольная работа №5 по теме «Окружность» Вариант 2

1. 𝑀𝑁 и 𝑀𝐾 – отрезки касательных, проведенных к окружности радиуса 5 см. Найдите длины отрезков 𝑀𝑁 и 𝑀𝐾, если 𝑀𝑂 = 13 см.

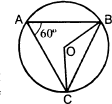2. На рисунке ∪ 𝐴𝐵 ∶ ∪ 𝐵𝐶 = 5 ∶ 3.

Найдите ∠𝐵𝑂𝐶, ∠𝐴𝐵𝐶.

1. Хорды 𝐴𝐵 и 𝐶𝐷 пересекаются в точке 𝐹 так, что 𝐴𝐹 = 4 см, 𝐵𝐹 = 16 см, 𝐶𝐹 = 𝐷𝐹. Найдите

𝐶𝐷.

1. Окружность с центром 𝑂 и радиусом 12 см описана около треугольника 𝑀𝑁𝐾 так, что

∠𝑀𝑂𝑁 = 120°, ∠𝑁𝑂𝐾 = 90°. Найдите стороны 𝑀𝑁 и 𝑁𝐾 треугольника.