План учебного занятия
Тема учебного занятия: Взаимное расположение точек, прямых и плоскостей: аксиомы стереометрии.
Цели:
Обучающая: способствовать развитию навыков аналитического и образного мышления; закрепить знания учащихся о взаимном расположении точек, прямых и плоскостей в пространстве.
Развивающая: развитие привычки самостоятельной подготовки к занятиям, учить сравнивать и обобщать изучаемые факты и понятия, развитие познавательного интереса и пространственного мышления учащихся.
Воспитательная: создать условия для развития коммуникативных компетенций учащихся (культуры общения, умения работать в парах); способствовать развитию творческой деятельности учащихся, интереса к учебным занятиям по дисциплине «Математика» и самообразованию.
Методическая: использование на занятии информационно-компьютерных технологий для активизации познавательной деятельности учащихся.
Тип учебного занятия: комбинированное
Методы и приемы обучения: информационно-аналитический, репродуктивный.
В результате изучения темы учащиеся должны:
Знать:
основные фигуры стереометрии;
правила обозначения основных фигур;
аксиомы стереометрии;
следствия из аксиом стереометрии.
Уметь:
распознавать пространственные геометрические фигуры;
раскрывать сущность геометрических понятий;
формулировать аксиомы стереометрии и следствия из них;
объяснять способы задания плоскости и соотношение принадлежности прямой и плоскости;
иллюстрировать условие задачи;
применять теоретические сведения при решении задач;
решать задачи на построение точки пересечения прямой и плоскости, прямой пересечения плоскостей.
Методическое и материально-техническое обеспечение учебного занятия: учебники, макеты многогранников, карточки с индивидуальными заданиями (многогранники, самостоятельная работа), компьютер, мультимедийный проектор, мультимедийное сопровождение учебного занятия.
Междисциплинарные связи: с учебной дисциплиной «История».
| Дидактическая структура занятия | Методическая подструктура |
| Методические приемы, их содержание | Методы обучения | Средства обучения | Способы организации деятельности учащихся |
Организационный этап | Организация начала занятия. Подготовка к совместной коммуникативной деятельности учащихся и преподавателя Проверка присутствующих учащихся и их готовности к занятию | Информационно-аналитический
| Предъявление информации через слово преподавателя | Фронтальная, учащиеся проявляют готовность к учебному занятию |
Целевая установка. Мотивация учебной деятельности учащихся. | Сообщение темы занятия. Обсуждение целей учебно-познавательной деятельности учащихся (быстро). Знакомство с этапами работы, а также с критериями оценки учебной деятельности учащихся при выполнении контрольной работы | Информационно-аналитический
| Предъявление информации через слово преподавателя | Фронтальная, анализируется готовность учащихся к активной учебно-познавательной деятельности на основе опорных знаний |
Актуализация знаний | Актуализация опорных знаний. Установление правильности и осознанности выполнения домашнего задания всеми учащимися, выявление пробелов и их коррекция. | Информационно-аналитический
| Результаты выполнения домашнего задания. | Фронтальная, анализируется процент выполнения и правильность выполнения домашнего задания. |
Проверка уровня сформированности общеучебных знаний, умений и навыков. | Проверка домашнего задания: | Репродуктивный
| Перечень вопросов для диктанта и для фронтального опроса; карточки с индивидуальными заданиями | Фронтальная и индивидуальная; учащиеся отвечают на вопросы математического диктанта, выполняют проверку; самостоятельно выполняют задания по карточкам. |
Формирование новых знаний, умений и навыков. | Выполнение устно заданий по готовым рисункам Задачи №1, 2, 3, 4, 5.
| Репродуктивный | Мультимедийная презентация | Фронтальная, учащиеся под руководством преподавателя выполняют задания устно |
Работа по готовым рисункам Задачи №1, 2, 3, 4 | Репродуктивный | Мультимедийная презентация | Фронтальная, учащиеся под руководством преподавателя выполняют задания в тетрадях. |
Выполнение заданий по учебнику [6] глава 1 §2 стр. №71; №73 §3 стр. №111; №112 Дополнительно §2 стр. №75 | Репродуктивный | Учебники, изображения многогранников на доске | Фронтальная, учащиеся под руководством преподавателя выполняют задания у доски. |
Закрепление полученных знаний. | Работа по карточкам | Репродуктивный | Карточки для индивидуальной работы | Индивидуальная, учащиеся самостоятельно выполняют задания по карточкам. |
Подведение итогов занятия. | Информирование о домашнем задании. Осмысление содержания и порядка выполнения домашнего задания. [6], глава 1 §2-3 №72, 74, 113 | Информационно-аналитический | План занятия | Фронтальный, учащиеся осознают необходимость выполнения домашнего задания. |
Оценка знаний учащихся и выставление отметок.
| Информационно-аналитический
| Критерии оценки | Индивидуальный, учащиеся сознают успешность выполненных учебных заданий |
Рефлексия. Самоанализ собственной деятельности на учебном занятии учащимися. | Информационно-аналитический | Слово преподавателя, карточки для рефлексии | Фронтальная, учащиеся осознают результаты своей деятельности |
ХОД УЧЕБНОГО ЗАНЯТИЯ
Организационный этап.
Организация начала занятия.
Подготовка к совместной коммуникативной деятельности учащихся и преподавателя.
Проверка присутствующих учащихся и их готовности к занятию.
Целевая установка. Мотивация учебной деятельности учащихся.
Сообщение темы занятия.
Тема нашего учебного занятия «Взаимное расположение точек, прямых и плоскостей в пространстве: аксиомы стереометрии».
Обсуждение целей учебно-познавательной деятельности учащихся (быстро).
Сегодня на занятии мы закрепим наши знания по теме «Аксиомы стереометрии». Эта тема открыла вам знакомство с новым разделом геометрии – «Стереометрия», который мы будем изучать на протяжении всего курса изучения учебной дисциплины «Математика». Сегодня мы повторим взаимное расположение точек, прямых и плоскостей в пространстве, рассмотрим геометрические тела, вспомним некоторые их свойства, повторим аксиомы стереометрии и следствия из них, будем формировать навыки применения аксиом стереометрии и их следствий при решении задач.
И как сказал великий русский ученый Михаил Васильевич Ломоносов «Математику уже затем учить надо, что она ум в порядок приводит».
Знакомство с этапами работы, а также с критериями оценки учебной деятельности учащихся при выполнении контрольной работы.
Наше занятие мы построим следующим образом:
проверим домашнее задание путем написания математического диктанта, фронтального опроса, индивидуальной работы по карточкам;
заслушаем сообщения учащихся об аксиоматическом методе в геометрии;
узнаем, как вы справились с дополнительным домашним заданием по подготовке математических сказок и стихов, а также узнаем ответы на вопросы исторической викторины;
научимся работать с готовыми рисунками;
научимся применять аксиомы стереометрии и следствия из них при решении задач.
Актуализация знаний.
Актуализация опорных знаний.
Установление правильности и осознанности выполнения домашнего задания всеми учащимися, выявление пробелов и их коррекция.
Все выполнили домашнее задание?
Какие вопросы возникли при выполнении домашнего задания?
Проверка уровня сформированности общеучебных знаний, умений и навыков.
Проверка домашнего задания.
Математический диктант с самопроверкой (приложение 1).
Фронтальный опрос (приложение 2, вопросы 1-20).
Историческая справка «Аксиомы. Аксиоматический метод» (приложение 3).
Просмотр видеоролика «Ералаш. Аксиома».
Фронтальный опрос (приложение 2, вопросы 21-28).
Анализ выполнения дополнительного домашнего задания:
определите, о каких аксиомах или следствиях из аксиом идет речь (приложение 4);
чтение учащимися стихов и сказок, которые они сочинили дома.
Формирование знаний, умений и навыков.
Итак, мы повторили взаимное расположение точек, прямых и плоскостей в пространстве, рассмотрели геометрические тела, повторили аксиомы стереометрии и следствия из них. А сейчас будем применять аксиомы стереометрии и их следствия при решении задач на нахождение и построение точки пересечения прямой и плоскости, на нахождение и построение прямой пересечения плоскостей.
Решение задач по готовым рисункам (устно).
| Задача №1 | Пользуясь данным рисунком, назовите: а) четыре точки, лежащие в плоскости SAB, в плоскости АВС; б) плоскость, в которой лежит прямая MN, прямая КМ; в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB. | 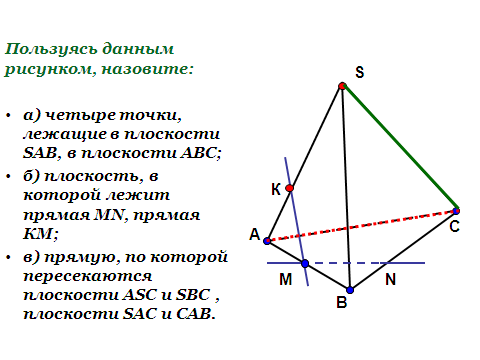
|
| Задача №2 | Пользуясь данным рисунком, назовите: а) две плоскости, содержащие прямую DE, прямую EF; б) прямую, по которой пересекаются плоскости DEF и SBC; плоскости FDE и SAC; в) две плоскости, которые пересекает прямая SC. | 
|
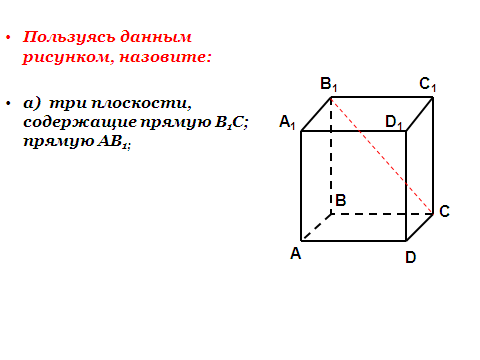
| Задача №3 | Пользуясь данным рисунком, назовите три плоскости, содержащие прямую В1С
| 
|
| Задача №4 | Пользуясь данным рисунком, назовите: несколько точек, которые лежат в плоскости α; несколько точек, которые не лежат в плоскости α; несколько прямых, которые лежат в плоскости α; несколько прямых, которые не лежат в плоскости α; несколько прямых, которые пересекают прямую ВС; несколько прямых, которые не пересекают прямую ВС. | 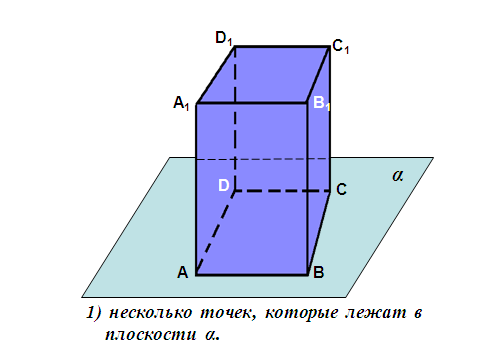
|
| Задача №5 | Определите и сформулируйте аксиомы или следствия из них по схематическому рисунку. | 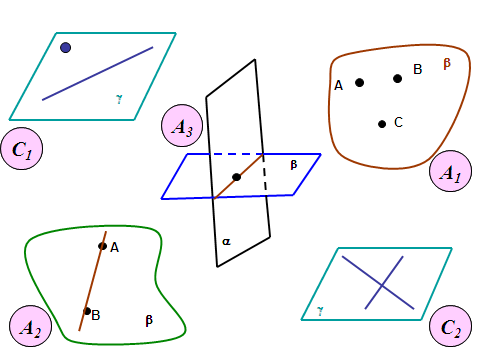
|
Решение задач по готовым рисункам.
Задача №1.
| Дан куб АВСDA1B1C1D1. Точка М лежит на ребре DD1. Точка N лежит на ребре CC1. Точка K лежит на ребре BB1 Назовите плоскости в которых лежат точка М, точка N. Найдите точку F – точку пересечения прямых MN и DС. Каким свойством обладает точка F? Найдите точку пересечения прямой KN и плоскости АВС. Найдите линию пересечения плоскостей MNK и ABC. | 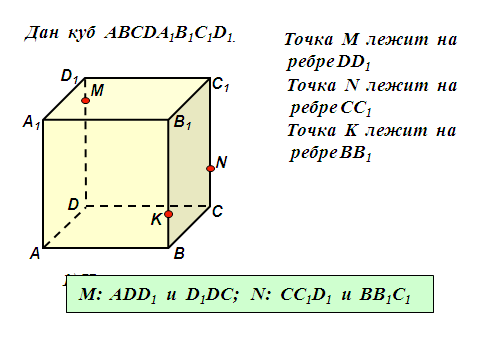
|
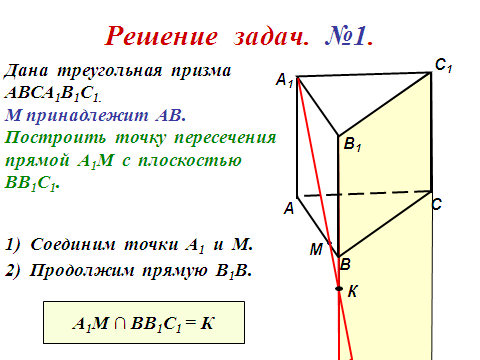
Задача №2.
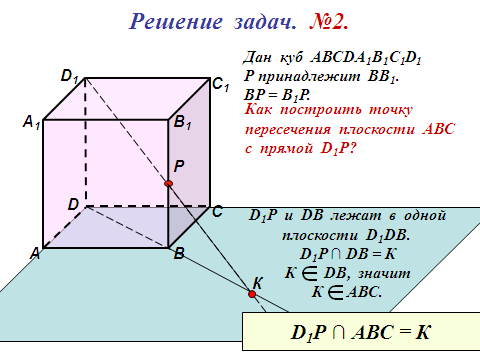
Задача №3.
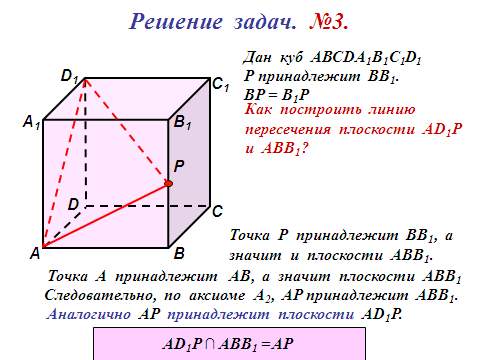
Задача №4.
Решение задач из учебника.
[6], глава 1 §2-3 № 71, 73, 111, 112
Дополнительно №75
Контроль усвоения изученного материала, обсуждение допущенных ошибок и их коррекция.
Работа по карточкам. (Приложение 7).
Подведение итогов занятия.
Викторина. (Приложение 8).
Просмотр видеоролика “Евклид”.
Информирование о домашнем задании.
Осмысление содержания и порядка выполнения домашнего задания.
[6], глава 1 §2-3 № 72, 74, 113
Дополнительно: Найти ответ на вопрос «Где в практической деятельности человека используются аксиомы стереометрии?»
Оценка знаний учащихся и выставление отметок.
Рефлексия.
Самоанализ собственной деятельности на учебном занятии учащимися.
Приложение 1
Математический диктант с самопроверкой.
Перечень вопросов
раздел геометрии, который изучает свойства фигур на плоскости… (планиметрия)
раздел геометрии, который изучает свойства фигур в пространстве… (стереометрия)
геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников, любые два смежные из которых не лежат в одной плоскости… (многогранник)
многогранник, имеющий шесть граней, которые являются равными квадратами… (куб)
многогранник, у которого шесть граней и каждая из них - параллелограмм… (параллелепипед)
параллелепипед, у которого боковые грани прямоугольники… (прямой параллелепипед)
параллелепипед, у которого все грани прямоугольники… (прямоугольный параллелепипед)
многогранник, у которого две грани равные многоугольники, а остальные грани - параллелограммы… (призма)
призма, у которой боковые грани - прямоугольники… (прямая призма)
призма, у которой боковые грани - прямоугольники, а ее основания – правильные многоугольники… (правильная призма)
многогранник, у которого одна грань - многоугольник, а остальные грани треугольники с общей вершиной… (пирамида)
пирамида, у которой основание – правильный многоугольник, а все боковые ребра равны между собой… (правильная пирамида)
треугольная пирамида, у которой все грани – равные правильные треугольники… (тетраэдр).
ОТВЕТЫ
Планиметрия
Стереометрия
Многогранник
Куб
Параллелепипед
Прямой параллелепипед
Прямоугольный параллелепипед
Призма
Прямая призма
Правильная призма
Пирамида
Правильная пирамида
Тетраэдр
Приложение 2
Фронтальный опрос.
Перечень вопросов:
Какие разделы геометрии вы знаете?
Ответ: планиметрия и стереометрия.
Дайте определение понятию «планиметрия».
Ответ: планиметрия – раздел геометрии, который изучает свойства фигур на плоскости.
Дайте определение понятию «стереометрия».
Ответ: стереометрия – раздел геометрии, который изучает свойства фигур в пространстве.
Назовите основные фигуры на плоскости.
Ответ: Основные фигуры на плоскости – точка и прямая.
Назовите основные фигуры в пространстве.
Ответ: Основные фигуры на плоскости – точка, прямая и плоскость.
Что дает нам наглядное представление об основных фигурах в пространстве?
Ответ: Геометрические тела.
Какие геометрические тела вы знаете?
Ответ: Многогранники и тела вращения.
С какими геометрическими телами мы познакомились.
Ответ: Многогранники.
Какое геометрическое тело называется многогранником?
Ответ: Многогранник – это геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников, любые два смежные из которых не лежат в одной плоскости.
Назовите виды многогранников, которые вы знаете.
Ответ: Призма, пирамида.
Какой многогранник называется кубом?
Ответ: Куб – многогранник, имеющий шесть граней, которые являются равными квадратами.
Какой многогранник называется параллелепипедом?
Ответ: Параллелепипед – многогранник, у которого шесть граней и каждая из них - параллелограмм.
Какой параллелепипед называется прямым?
Ответ: Прямой параллелепипед – это параллелепипед, у которого боковые грани прямоугольники.
Какой параллелепипед называется прямоугольным?
Ответ: Прямоугольный параллелепипед – это параллелепипед, у которого все грани прямоугольники.
Какой многогранник называется призмой?
Ответ: Призма – это многогранник, у которого две грани равные многоугольники, а остальные грани - параллелограммы.
Какая призма называется прямой?
Ответ: Прямая призма – это призма, у которой боковые грани - прямоугольники.
Какая призма называется правильной?
Ответ: Правильная призма – это призма, у которой боковые грани - прямоугольники, а ее основания – правильные многоугольники.
Какой многогранник называется пирамидой?
Ответ: Пирамида – это многогранник, у которого одна грань - многоугольник, а остальные грани треугольники с общей вершиной.
Какая призма называется правильной?
Ответ: Правильная пирамида – это пирамида, у которой основание – правильный многоугольник, а все боковые ребра равны между собой.
Какая пирамида называется тетраэдром?
Ответ: Тетраэдр – это треугольная пирамида, у которой все грани – равные правильные треугольники.
Какое утверждение называется аксиомой?
Ответ: Аксиома – исходное положение научной теории, принимаемое без доказательства.
Сколько аксиом стереометрии мы знаем?
Ответ: Три.
Сформулируйте аксиомы стереометрии?
Ответ:
А1.Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей
Сформулируйте следствия из аксиом стереометрии?
Ответ:
Сл1.Через прямую и не лежащую на ней точку проходит единственная плоскость.
Сл2. Через две пересекающиеся прямые проходит единственная плоскость.
Что описывают аксиомы стереометрии?
Ответ:
А1.Способ задания плоскости.
А2. Взаимное расположение прямой и плоскости.
А3. Взаимное расположение плоскостей.
Сформулируйте способы задания плоскости? Покажите на рисунке.
Ответ: 1) через три точки; 2)через прямую и не лежащую на ней точку; 3) через две пересекающиеся прямые.
Каково взаимное расположение прямой и плоскости в пространстве? Покажите на рисунке.
Ответ: 1) прямая лежит в плоскости; 2)прямая пересекает плоскость; 3) прямая не пересекает плоскость.
Сколько общих точек в каждом случае? Покажите на рисунке.
Ответ: 1) множество; 2)одна; 3) ни одной.
Приложение 3
Аксиоматический метод построения геометрии
Изучаемая нами геометрия является иллюстрацией метода построения теории, которая получила название аксиоматического метода.
К началу III в. до н. э. в работах древнегреческого ученого Аристотеля была сформулирована идея построения научной теории. Применительно к геометрии ее реализовал Евклид в своей работе «Начала». На основании накопленных к тому времени фактов и знаний он выделил и сформулировал несколько утверждений (постулатов), принимаемых без доказательств, из которых выводились их логические следствия в виде теорем. Система Евклида явилась первым опытом применения аксиоматического метода и просуществовала без изменений до XIX века н. э. Однако она обладала рядом недостатков с современной точки зрения на аксиоматический метод, и на рубеже XIX–XX веков была построена геометрическая система, свободная от этих недостатков.
Суть аксиоматического метода построения научной теории состоит в следующем:
перечисляются основные (неопределяемые) понятия,
все вновь возникающие понятия должны быть определены через основные понятия и понятия, определенные ранее.
Основные понятия делятся на два вида: одни обозначают объекты, которыми занимается теория, другие обозначают отношения между ними. Так, точка и прямая – это объекты геометрии, а то, что точка принадлежит прямой, – отношение между ними. Необходимость введения основных понятий очевидна, так как процесс, состоящий в том, чтобы определить одни объекты через другие, более простые, а эти в свою очередь через еще более простые, не будет ограничен до тех пор, пока некоторые объекты не будут считаться неопределимыми.
Далее формулируются аксиомы – предложения, принимаемые без доказательства. Доказывая какое-либо утверждение, опираются на некоторые предпосылки, которые считаются известными. Но эти предпосылки необходимо, в свою очередь, обосновать, опираясь на другие, и т. д. Чтобы оборвать эту бесконечную последовательность, вводят аксиомы – предпосылки, которые принимаются за исходные и составляют основу для доказательства теорем. Все остальные предложения должны являться логическим следствием аксиом или ранее доказанных утверждений.
К середине XIX века основания евклидовой геометрии оставались на том же уровне, как они были изложены в работах Евклида. Однако общая тенденция к повышению математической строгости во второй половине XIX века побудила многих авторов к пересмотру основ геометрии с целью предложить полную, непротиворечивую, независимую систему аксиом. Наибольшее признание среди различных сформулированных систем получила аксиоматика немецкого математика Давида Гильберта, изложенная в его книге «Основания геометрии» в 1899 г. Ему удалось построить аксиоматику геометрии, расчлененную настолько естественным образом, что логическая структура геометрии становилась совершенно прозрачной: три группы аксиом управляют каждая своим основным отношением – принадлежности, порядка, равенства. Такое расчленение позволило, во-первых, формировать аксиомы кратким и простым образом; во-вторых, исследовать, как далеко можно развить геометрию, если положить в основу не всю аксиоматику, а только ту или иную ее группу. При этом система задавала действительно абстрактную теорию, в которой объекты и отношения между ними – это просто какие-то мыслимые «вещи», про которые известно только то, что они удовлетворяют аксиомам.
Наряду с системой аксиом Гильберта можно назвать и другие варианты аксиоматики евклидовой геометрии: аксиоматика, предложенная в 1904 году Фридрихом Шуром и основанная на понятии движения (наложения), аксиоматика, основанная на понятии о численном расстоянии, предложенная тогда же Вениамином Федоровичем Каганом, векторная аксиоматика Германа Вейля и др.
Несмотря на то, что вопрос о формулировке непротиворечивой, полной и независимой системы аксиом геометрии был решен, выбор «удобной» системы остается открытым еще и с точки зрения методики и наглядности изложения материала, т. е. с точки зрения педагогики. В связи с этим необходимо заметить, что изучаемая нами система аксиом не является полной.
При подготовке к занятию мы обратили внимание на аксиому параллельности прямых. Независимость аксиомы о параллельных прямых в рамках аксиоматики евклидовой геометрии удалось установить только в XIX веке, после двух тысячелетий попыток вывести ее как следствие других аксиом системы. Хотя и сейчас многие задумываются над ее содержанием.
(Просмотр видеоролика - Ералаш)
Приложение 4
Анализ выполнения дополнительного домашнего задания.
Определите, о каких аксиомах или следствиях из аксиом идет речь:
На трех морях живут киты,
На синих трех морях.
На трех китах стоит Земля,
На трех больших китах.
Три точки – это якоря
Для плоскости одной.
И хоть в китов не верю я,
Но пусть по плоскости меня
Сейчас троллейбус номер «три»
Быстрей умчит.
Ответ: Аксиома А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Говорит прямой прямая:
- Я единственная знаю,
Как в далекий путь с тобой,
Даже в плоскости одной,
Мне отправиться, сестрица…
Точка А тут пригодится.
Не знакома с нею ты,
Ну, да это полбеды;
Раз нам, видно, все равно
Пересечься не дано,
Пусть она хоть в том поможет,
Что единый курс проложит!
Ответ: Аксиома 3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Чтение учащимися стихов и сказок, которые они сочинили дома.
Приложение 5
| Ф.И. учащегося ______________________________________________________________
|
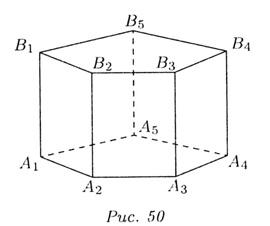
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
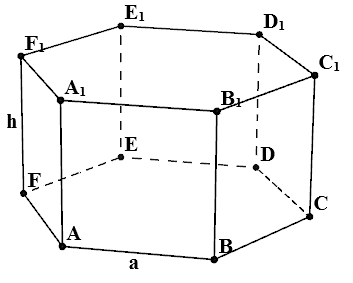
| Запишите: Название многогранника _________________ ______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
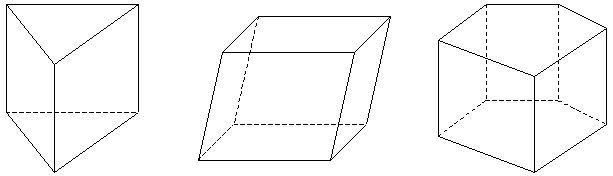
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
|
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ ______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
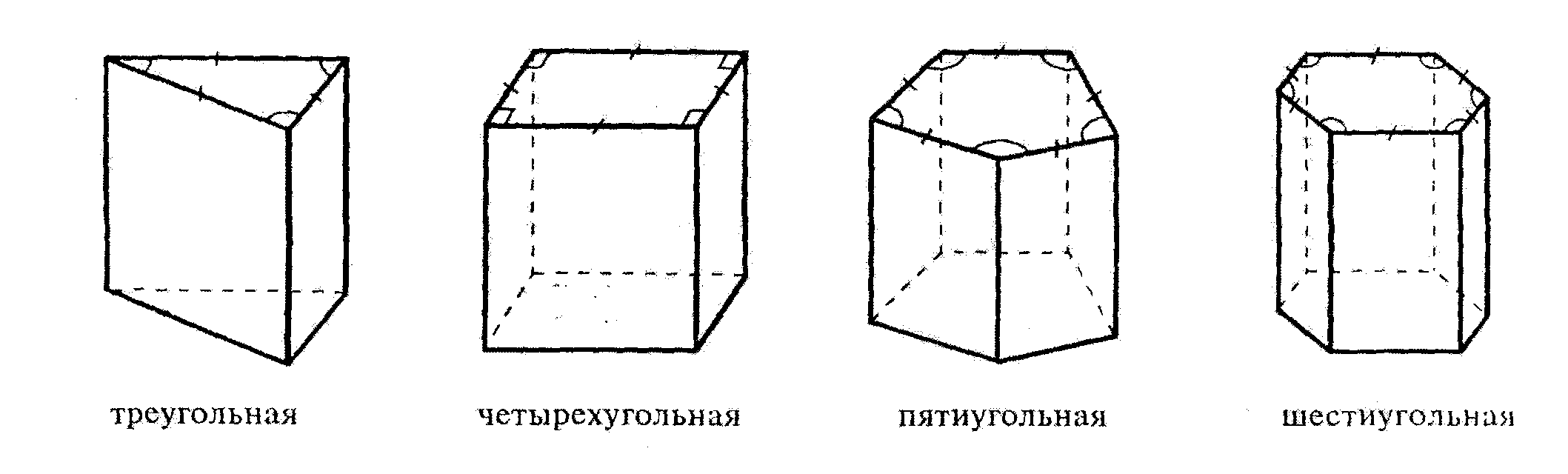
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
|
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ ______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
|

|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
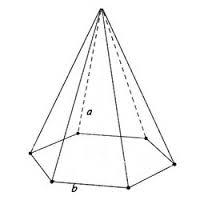
| Запишите: Название многогранника _________________ ______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
|
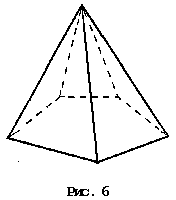
|
| Ф.И. учащегося ______________________________________________________________
|
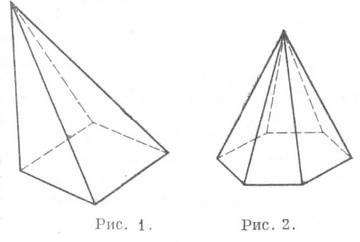
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ ______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
|
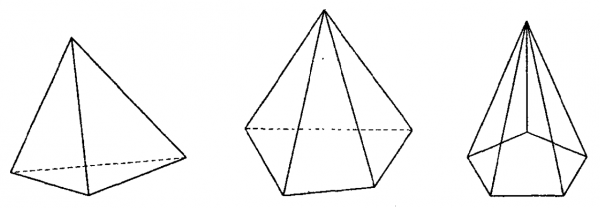
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ ______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| 
|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
|

|
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ _______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| |
| Ф.И. учащегося ______________________________________________________________
|
| Запишите: Название многогранника _________________ ______________________________________ Количество вершин _____________________ Перечислите вершины ___________________ _______________________________________ Количество ребер _______________________ Перечислите ребра ______________________ _______________________________________ Количество граней ______________________ Перечислите грани ______________________ _______________________________________
| |
Приложение 6

Приложение 7
Вариант 1
Ф.И. учащегося ______________________________________________________________
| Дано: | N (DBC) (DBC) |
| Построить: | MN∩(ABC) |
| Построение: |
|

Вариант 2
Ф.И. учащегося ______________________________________________________________
| Дано: | К B1B B1B |
| Построить: | а) KM∩(ABC) б) NK∩(ABC) |
| Построение: |
|
Вариант 3
Ф.И. учащегося ______________________________________________________________

| Дано: | N (DBC) (DBC) |
| Построить: | MN∩(ABC) |
| Построение: |
|
Вариант 4
Ф.И. учащегося ______________________________________________________________
| Дано: | P (ADC), N (ADC), N (DBC) (DBC) |
| Построить: | PN∩(ABC) |
| Построение: |
|
Вариант 5
Ф.И. учащегося ______________________________________________________________
| Дано: | P (NKL), F (NKL), F (NML) (NML) |
| Построить: | PF∩(KML) |
| Построение: |
|
Вариант 6
Ф.И. учащегося ______________________________________________________________
| Дано: | M AA1C1C AA1C1C |
| Построить: | A1M∩(CC1B) |
| Построение: |
|
Вариант 7
Ф.И. учащегося ______________________________________________________________
| Дано: | A α, B α, B β β |
| Построить: | а) α∩(MAB) б) β∩(MAB) |
| Построение: |
|

Вариант 8
Ф.И. учащегося ______________________________________________________________
| Дано: |
|
| Построить: | (MNK)∩(ABC) |
| Построение: |
|
Вариант 9
Ф.И. учащегося ______________________________________________________________
| Дано: |
|
| Построить: | (MNK)∩(ABC) |
| Построение: |
|
Приложение 8
Викторина по истории геометрии
ВОПРОСЫ
1. Кто, по преданию, из великих геометров древности сказал вражескому солдату, пришедшему его убить: «Не тронь моих кругов»?
Архимед, погибший при захвате римлянами его родного города Сиракузы в то время, когда пришел римский солдат. По преданию, Архимед был увлечен решением геометрической задачи, чертеж которой был выполнен на песке. Солдат, убивший Архимеда, или не знал о приказе военачальника сохранить жизнь Архимеду, или не узнал Архимеда. Впоследствии этот солдат был наказан, а семья Архимеда была окружена почестями.
2. На каком здании были начертаны слова: «Да не войдет сюда не искусившийся в геометрии!»
По преданию, эти слова были написаны у входа в Академию Платона (429-348 гг. до н.э.), чрезвычайно ценившего математику и способствовавшего его развитию. «Академией» называлась философская научная школа, основанная Платоном в 6 веке до н.э. близ Афин, в садах, посвященных памяти героя Академа.
3. Что, по преданию, завещал высечь на своем надгробном камне Архимед?
Архимед завещал высечь чертеж к теореме о свойствах шара и цилиндра. Он установил, что объем шара равен удвоенному объему конуса с радиусом основания, равным радиусу шара, и высотой, равной диаметру шара или 2/3 объема цилиндра с таким же радиусом основания и такою же высотой. Эти три тела с данным соотношением называют «телами Архимеда». Римский военачальник Марцелл исполнил желание ученого, воздвигнув в его честь гробницу, на которой был изображен шар, вписанный в цилиндр.
4. Кто является создателем первой неевклидовой геометрии? Когда и где она впервые была изложена?
Н.И. Лобачевский (1792-1856). На заседании физико-математического факультета Казанского университета 11(23) февраля 1826 г. Лобачевский сделал доклад об основах геометрии.
5. Кто является основоположником аналитической геометрии, являющейся соединением алгебры с геометрией?
Рене Декарт (1596-1650), французский философ и математик.
6. Кто ввел термины «абсцисса», «ордината», «координата»?
Лейбниц ввел понятия «абсцисса» в 1665 г., «ордината» - в 1684 г., «координата» - 1692 г.
7. Кто является автором самого первого учебника геометрии? Он же является однофамильцем известного греческого медика.
Гиппократ.
8. Этот ученый больше известен своими открытиями в алгебре, тем не менее, на своем надгробном памятнике он завещал выгравировать правильный 17-угольник, вписанный в круг. О каком ученом идет речь?
О Карле Фридрихе Гауссе – немецком математике.
9. Назовите фамилию древнегреческого ученого, предложившего формулу для нахождения площади треугольника по трем сторонам.
Герон.
10. Какая книга лежит в основе большинства школьных учебников по геометрии? Кто её автор?
«Начала» Евклида, написанные в 6 веке до н.э.
11. Кто является создателем современной аксиоматики геометрии Евклида?
Д. Гильберт (1862-1943), немецкий математик.
12. Кто автор слов «В геометрии нет особых путей для царей!»? В связи с чем они были произнесены?
Автор этих слов – Евклид. Он произнес их Птоломею, спросившему у Евклида однажды, нет ли в геометрии более краткого пути, чем его «Начала».












































