10 класс
№ 5
Тема урока:
Аксиомы стереометрии.
Цель урока: ♦ рассмотреть пространственные аксиомы С1 – С3 и стереометрические аналоги
планиметрических аксиом I1 – I2;
♦ повторить аксиомы планиметрии;
♦ научить применять аксиомы стереометрии при решении задач.
Оборудование: чертёжные инструменты; компьютер; проектор, экран.
ХОД УРОКА.
1.Организация начала урока.
2. Сообщение темы и цели урока.
● Мы начинаем изучение систематического курса следующего раздела геометрии –
стереометрии. На какие вопросы мы должны сегодня получить ответы: Что изучает
стереометрия? Каковы основные фигуры стереометрии? Какими основными свойствами они
обладают?
3.Изучение нового материала.
Стереометрия – это раздел геометрии, в котором изучаются фигуры в пространстве.
В стереометрии, также как и в планиметрии, свойства геометрических фигур устанавливаются путём доказательства соответствующих теорем.
При этом отправными являются свойства основных геометрических фигур, сформулированных в виде аксиом.
Аксиомы – это первоначальные факты геометрии, которые принимаются без доказательств и позволяют вывести из них дальнейшие факты этой науки.
По словам Аристотеля: «Аксиомы обладают наивысшей степенью общности и представляют начала всего»
Фридрих Энгельс говорил, что «Так называемые аксиомы математики – это те немногие мыслительные определения, которые необходимы в математике в качестве исходного пункта».
Логически безупречный список аксиом геометрии был указан на рубеже XIX – XX вв. немецким математиком Д. Гильбертом.
● Основными фигурами в пространстве являются точка, прямая и плоскость. О точке и
прямой мы вели разговор на уроках планиметрии. Остановимся теперь на плоскости.
● Плоскость мы представляем себе как ровную поверхность крышки стола, доски и т. д.
Изображать плоскость мы будем в виде параллелограмма или в виде произвольной
области.


● Плоскость, как и прямая, бесконечна. На рисунке мы изображаем только часть плоскости,
но представляем её неограниченно продолженной во все стороны. Плоскости обозначают
греческими буквами 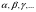
● Введение нового геометрического образа (плоскости) заставляет расширить, известную
нам в планиметрии, систему аксиом. Поэтому вводится группа аксиом С, которая
выражает основные свойства плоскости в пространстве. Эта группа состоит из трёх аксиом.
Сформулируем их.
С1: Какова бы ни была плоскость, существуют точки, принадлежащие этой
плоскости, и точки, не принадлежащие ей.

Например, на данном рисунке точки А и С принадлежат плоскости α, а точки D, B и K ей
не принадлежат.
С2: Если две различные плоскости имеют общую точку, то они пересекаются по
прямой, проходящей через эту точку.
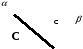
Этой аксиомой утверждается, что если две различные плоскости  и
и 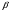 имеют общую точку С, то существует прямая c, принадлежащая каждой из этих плоскостей. При этом если точка С принадлежит обеим плоскостям, то она принадлежит прямой c.
имеют общую точку С, то существует прямая c, принадлежащая каждой из этих плоскостей. При этом если точка С принадлежит обеим плоскостям, то она принадлежит прямой c.
То есть совокупность всех общих точек плоскостей  и
и 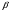 есть прямая, которая, конечно, проходит через указанную в аксиоме общую точку. Можно сказать иначе: общие точки плоскостей
есть прямая, которая, конечно, проходит через указанную в аксиоме общую точку. Можно сказать иначе: общие точки плоскостей  и
и 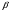 составляют прямую (но не просто лежат на одной прямой).
составляют прямую (но не просто лежат на одной прямой).
Независимо от способа выражения смысл аксиомы С2 в том, что если плоскости  и
и 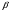 различны и пересекаются (имеют хотя бы одну общую точку), то их пересечением является прямая (а не какая-нибудь другая линия, фигура).
различны и пересекаются (имеют хотя бы одну общую точку), то их пересечением является прямая (а не какая-нибудь другая линия, фигура).
С3: Если две различные прямые имеют общую точку, то через них можно провести
плоскость, и притом только одну.

Это значит, что если две различные прямые имеют общую точку С, то существует плоскость 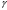 , содержащая прямые а и b. Плоскость, обладающая этим свойством, единственна.
, содержащая прямые а и b. Плоскость, обладающая этим свойством, единственна.
● Аксиомы выражают интуитивно ясные свойства плоскостей, их связь с двумя другими
основными фигурами стереометрии – с прямыми и точками.
● Рассмотренные аксиомы С1 – С3 относятся только к плоскостям, и к ним необходимо
добавить аксиомы о прямых, аналогичные соответствующим планиметрическим
аксиомам.
● Таким образом, система аксиом стереометрии состоит из аксиом планиметрии и группы
аксиом С.
3.Закрепление изученного материала.
№ 1,2
4. Итог урока.
- Что изучает стереометрия?
- Какие фигуры в стереометрии считаются основными?
- В виде каких утверждений формулируются свойства основных фигур стереометрии?
- Сформулируйте аксиомы группы С.
5. Домашнее задание.
№3,4








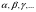

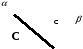
 и
и 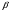 имеют общую точку С, то существует прямая c, принадлежащая каждой из этих плоскостей. При этом если точка С принадлежит обеим плоскостям, то она принадлежит прямой c.
имеют общую точку С, то существует прямая c, принадлежащая каждой из этих плоскостей. При этом если точка С принадлежит обеим плоскостям, то она принадлежит прямой c.
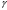 , содержащая прямые а и b. Плоскость, обладающая этим свойством, единственна.
, содержащая прямые а и b. Плоскость, обладающая этим свойством, единственна.


















