Алгебра жана анализдин башталышы

Повторение «Квадратичная функция и её график»

Определение

Функция

а, в, с - заданные числа, а=0, х -действительная переменная, называется квадратичной функцией

Свойства

• График
• Направление «ветвей»
• Вершина параболы
• Ось симметрии
• Нули функции
• Возрастание, убывание функции
• Положительные, отрицательные значения функции
• Построение графика квадратичной функции

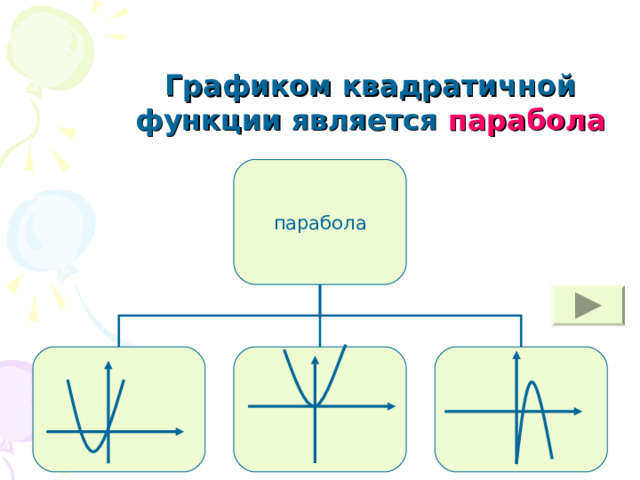
Графиком квадратичной функции является парабола

парабола

4

0, то «ветви» параболы направлены вверх у у 0 х х 0 " width="640"

Направление «ветвей» параболы

• Если а 0, то «ветви» параболы направлены вниз

• Если а 0, то «ветви» параболы направлены вверх

у

у

0

х

х

0

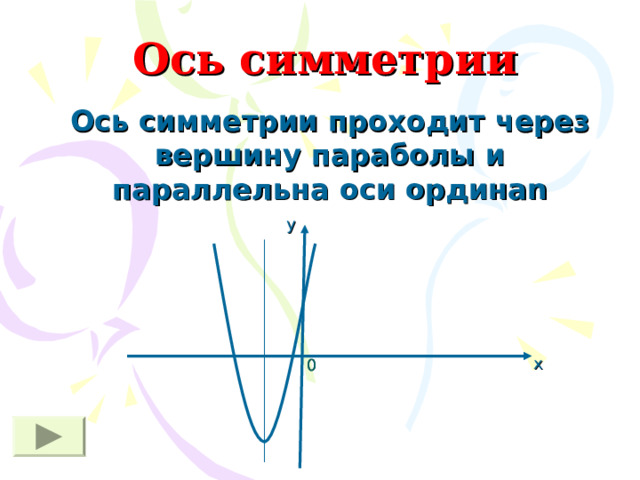
Ось симметрии

Ось симметрии проходит через вершину параболы и параллельна оси ордина n

у

х

0

Нули функции

Те значения х, при которых функция принимает значение, равное 0, называют нулями функции

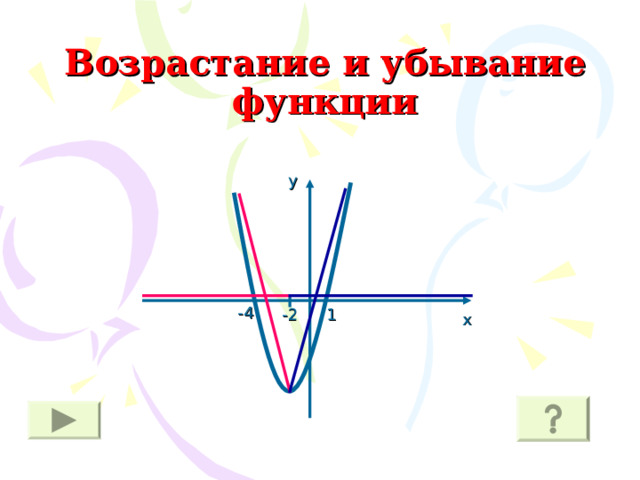
Возрастание и убывание функции

у

-4

-2

1

х

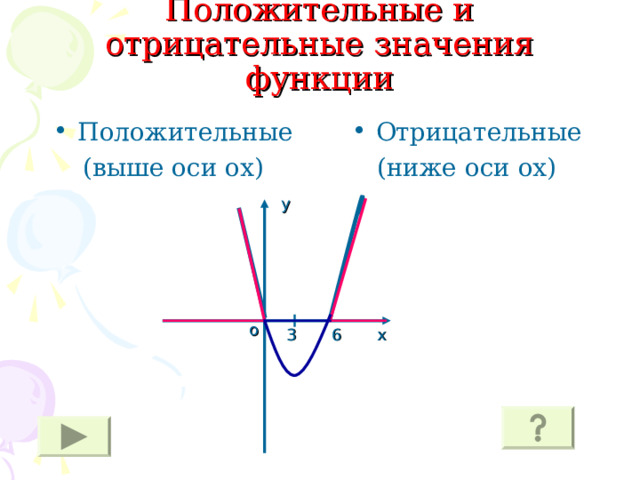
Положительные и отрицательные значения функции

• Положительные

• Отрицательные

(ниже оси ох)

(выше оси ох)

у

о

3

6

х

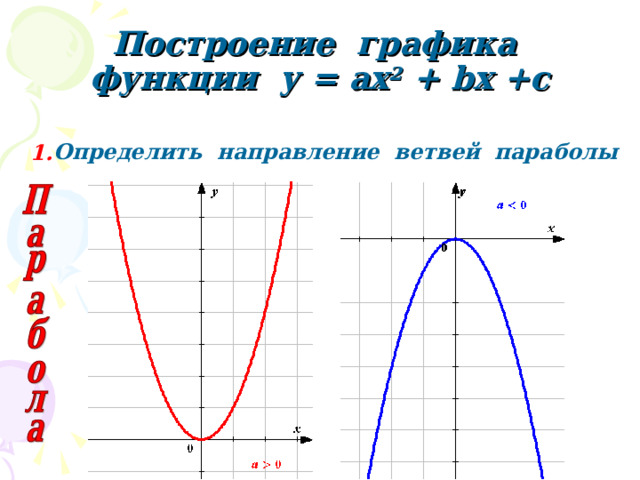
Построение графика функции у = ах 2 + b х +с

Определить направление ветвей параболы

1.

Построение графика функции у = ах 2 + b х +с

Найти координаты вершины параболы

(т; п).

2.

Провести ось

симметрии

3.

О (т;п)

Построение графика функции у = ах 2 + b х +с

Определить точки пересечения графика

функции с осью О х , т.е. найти нули

функции

4.

( х 1 ;0 )

( х 2 ;0 )

Построение графика функции у = ах 2 + b х +с

Составить таблицу значений функции

с учетом оси симметрии параболы

5.

х

х 1

у

х 2

у 1

х 3

у 2

х 4

у 3

у 4

Алгоритм построения графика функции у = ах 2 + b х +с

1.

Определить направление ветвей параболы.

Найти координаты вершины параболы

(т; п).

2.

3.

Провести ось симметрии.

Определить точки пересечения графика

функции с осью О х , т.е. найти нули

функции.

4.

5.

Составить таблицу значений функции

с учетом оси симметрии параболы.

Экзаменационный сборник: № 177 (1).

Задание

Запишите свойства функции

и постройте её график

• Направление «ветвей» - ветви вниз, т.к. -1
• Вершина параболы - А (-2; 9)
• Ось параболы х = -2
• Нули функции - -5 и 1
• Возрастает
• Убывает
• Положительные

значения

8. Отрицательные значения

y -5 -2 0 1 x

Домашнее задание:

Экзаменационный сборник

На «3»

№ 879

№ 878

На «4» и «5»

№ 178

№ 179

№ 183

• Каков вид графика функции

обратной пропорциональности?

1.

г

и

п

е

р

б

о

л

а

• Каков вид графика

квадратичной функции?

2.

п

1.

а

р

г

а

и

б

п

е

о

л

р

а

б

о

л

а

3.

3. Как называется

координата

точки по оси Ох?

а

б

2.

с

п

ц

а

1.

и

р

г

с

а

и

б

с

п

е

а

о

л

р

а

б

о

л

а

4.

о

3.

4. Как называется

координата

точки по оси Оу?

р

а

б

д

2.

и

п

с

ц

а

1.

н

и

а

р

г

с

а

т

и

с

б

п

а

е

о

а

л

р

а

б

о

л

а

4.

о

3.

5. Один из способов задания

функции.

р

а

б

д

2.

и

п

с

н

ц

а

1.

5.

ф

а

и

р

г

а

т

с

о

и

с

б

п

а

р

е

а

м

о

у

л

р

а

л

б

а

о

л

а

4.

о

3.

6. Переменная величина,

значение которой зависит

от изменения другой

величины.

а

р

6.

ф

д

б

2.

у

и

с

п

н

н

ц

а

1.

5.

к

а

и

р

ф

г

а

о

т

ц

с

и

и

с

б

п

а

р

е

а

я

о

м

л

у

р

л

а

б

а

о

л

а

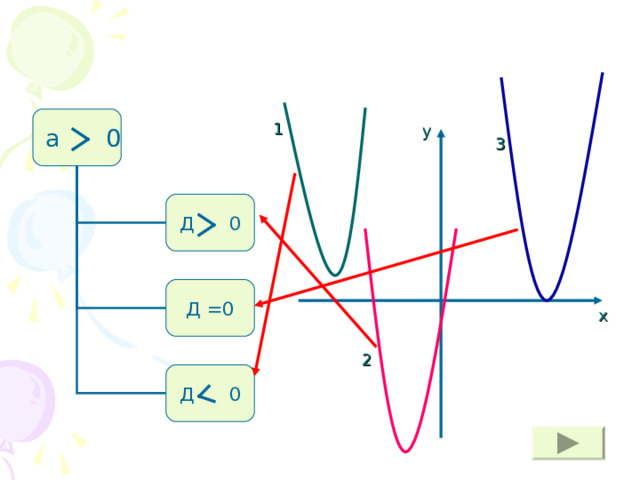
а 0

1

у

3

Д 0

Д =0

х

2

Д 0

25

у

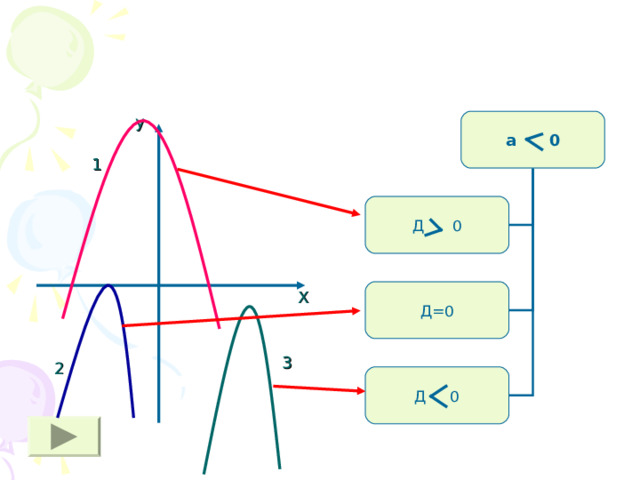
а 0

1

Д 0

Д=0

Х

3

2

Д 0

26

Какие функции являются квадратичными и почему?

Найти нули функции

• 0 и 1

2) нет нулей

3) -0,2 и 1

4) -3 и 3

0 2) вверх, т. к. 10 3) вверх, т. к. 4) вниз, т. к . -8 5) вниз, т. к . -1 " width="640"

Определить направление ветвей параболы

1) вверх, т. к. 4 0

2) вверх, т. к. 10

3) вверх, т. к.

4) вниз, т. к . -8

5) вниз, т. к . -1

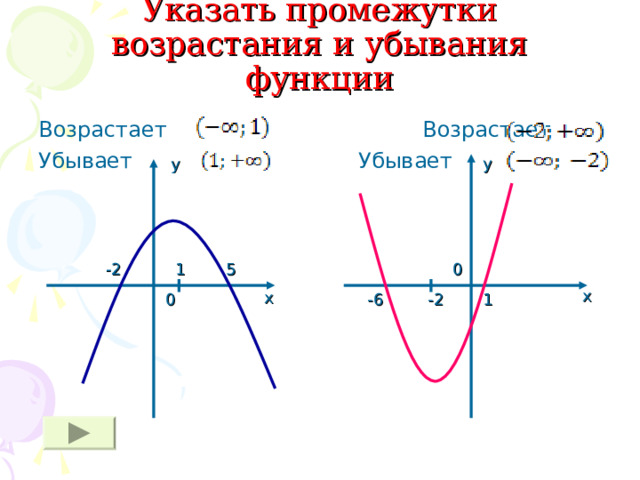
Указать промежутки возрастания и убывания функции

Возрастает Возрастает

Убывает Убывает

у

у

5

1

-2

0

х

х

1

-2

-6

0

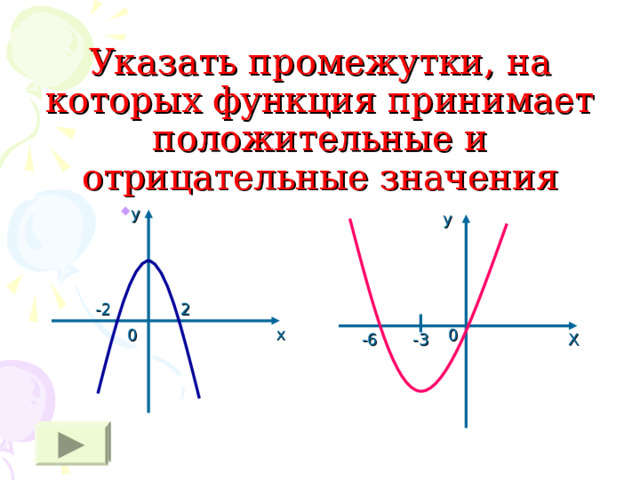
Указать промежутки, на которых функция принимает положительные и отрицательные значения

• у

у

2

-2

х

0

0

Х

-6

-3

• у

• у

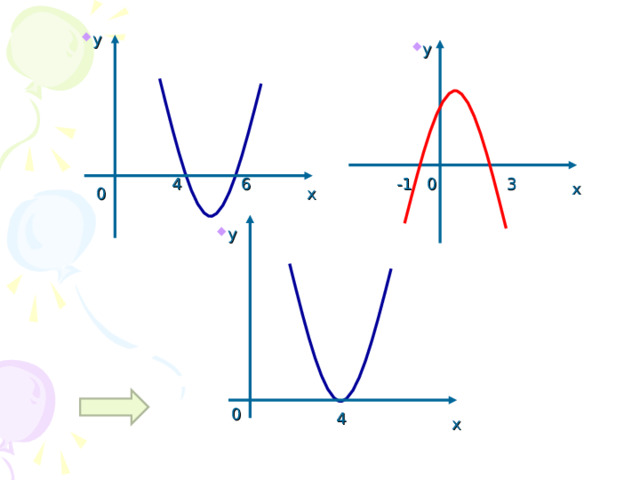
4

6

0

3

-1

х

0

х

• у

0

4

х

32

Найти координаты вершины параболы

1) А(-2; 1)

2) А (3;4)

3) А (2; 12)

Координаты вершины параболы