11.10.2016 АЛГЕБРА класс: 8б
Урок 17.Тема: «Алгебраические дроби ».
Цель урока:
образовательная - совершенствовать навыки действий с рациональными дробями; формировать умения выполнять тождественные преобразования рациональных выражений;
воспитательная - воспитывать чувство коллективизма и сопереживания успехам и неудачам своих товарищей;
развивающая - учить проводить доказательные рассуждения, используя математическую речь; учить умению сосредотачиваться на учебной деятельности и предупреждать ошибки по невнимательности (развивать самоконтроль); развивать творчество учеников.
Оборудование: раздаточный материал, маршрутные листы с критериями оценивания, цветные стикеры.
Тип урока: повторение, обобщение и систематизация пройденного материала
Формы работы: работа в малой группе, индивидуальная работа.
План урока:
Орг момент.
Актуализация.
Применение знаний
Творческое задание
Домашнее задание
Рефлексия
Орг момент.
Учащиеся рассаживаются в малые группы по принципу сильные, средние, слабые.
Учащиеся определяют тему и цели урока.
«Экспресс удачи»- пожелания друг другу на цветных стикерах.
Новые подходы в преподавании и обучении
Актуализация.
Заполнение таблицы ЗХУ.
Соотнеси термины и их формулировки
1
Целые выражения - это
1
Если числитель и знаменатель дроби умножить или разделить на одно и то же выражение, то получится равная ей дробь
2
Допустимые значения переменных - это
2
Перемножить числители и записать в числитель, перемножить знаменатели и записать в знаменатель
3
Рациональная дробь - это
3
Замена выражения другим, тождественно равным данному
4
Основное свойство дроби заключается в том, что
4
Нужно привести дроби к общему знаменателю и воспользоваться правилом сложения дробей с одинаковыми знаменателями
5
Чтобы перемножить дроби нужно
5
Выражения, составленные из чисел и переменных с помощью действий сложения, вычитания , умножения и деления на число, отличное от нуля
6
Преобразование выражения - это
6
Дробь, числитель и знаменатель которой многочлены
7
Чтобы сложить или вычесть дроби с разными знаменателями
7
Значения переменных, при которых выражение имеет смысл
Управление и лидерство в обучении.
Обучение критическому мышлению.
Применение знаний
Учащиеся сообща обсуждают задания, и распределяют их между собой.
Какая дробь называется рациональной?
Какие значения называются допустимыми значениями переменных?
Укажите допустимые значения переменной в выражении:
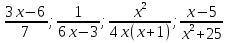
Сформулируйте основное свойство дроби?
Сократите дробь: 1) 2)
2)  3)
3) 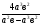
Найдите сумму и разность дробей
1)  2)
2)  3)
3)  4)
4) 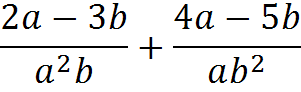
5)  6)
6)  7)
7) 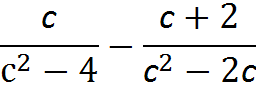
Как найти произведение алгебраических дробей?
Представьте в виде дроби:
 2)
2) 
Как выполнить деление алгебраических дробей?
Выполните деление:
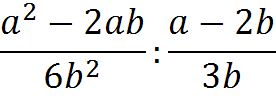 2)
2)  3)
3) 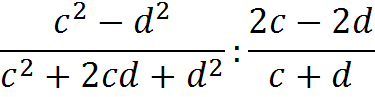
Как возвести алгебраическую дробь в степень?
Представьте в виде дроби:
 2)
2)  3)
3) 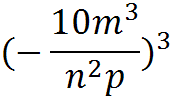
Самопроверка с помощью интерактива
Новые подходы в преподавании обучении.
Управление и лидерство в обучении.
Творческое задание Кроссворд.
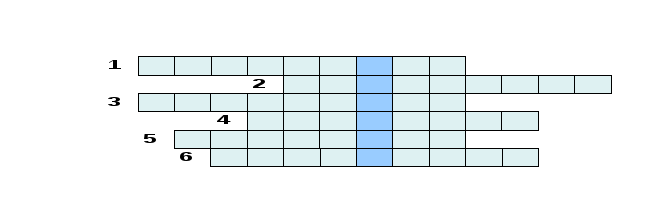
1. С помощью тождественных преобразований можно заменить исходное выражение тождественно равным выражением, более удобным для решения. То есть _________.
2. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их _________ ,
а знаменатель оставить прежним.
3. Равенство, верное при всех допустимых значениях входящих в него переменных называется ___________ .
4. Частное двух дробей равно произведению делимого на дробь, обратную ___________.
5. Как называются слагаемые многочлена, которые отличаются друг от друга только коэффициентом?
6. Что можно сделать с алгебраической дробью, если в состав числителя и знаменателя одновременно входит общий множитель?
Домашнее задание
Индивидуальные разноуровневые задания по карточкам
Обучение талантливы х и одаренных.
Рефлексия
Дополнить таблицу ЗХУ
Обучение критическому мышлению

















