Алгоритм по решению задач на поиск количества различных путей в графе, проходящих через город N

Алгоритм по решению задач на поиск количества различных путей в графе,

проходящих через город N.

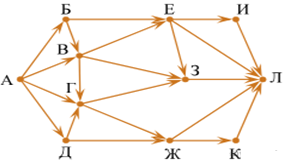
Задача. На рисунке  — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К и Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л, проходящих через город B?

Граф ориентированный. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком. Количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.

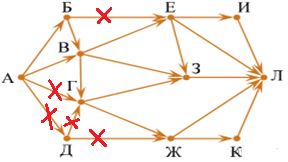
1. Убираем из рассмотрения те пути, которые не позволяют пройти через город В.

На рисунке вычёркиваем пути из Б в Е, из А в Г, из А в Д, из Д в Г, из Д в Ж.

1. Каждой вершине, начиная с начальной (А) ставим с соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1.

2. Применяем правило «индекс вершины равен сумме индексов его предков». Подсчитываем индекс только тех вершин, индексы предков которых уже посчитаны.

   3.1.индекс Б равен 1 (предок у Б один – вершина A)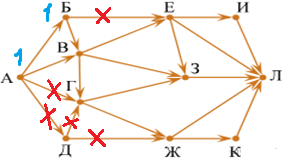
   3.2.индекс В равен 1+1=2 (предки вершины В – вершины A и Б).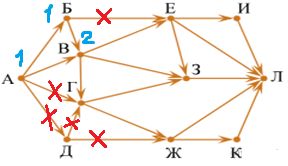
   3.3.индекс Г равен 2 (предок у вершины Г один – вершина В).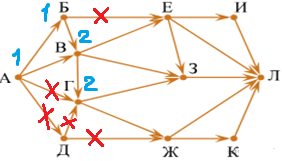
   3.4.индексы вершин Е и Ж равны 2 (предок у вершины Е один - вершина В, предок у вершины Ж один – вершина Г).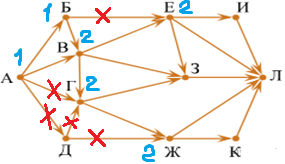
   3.5.индексы вершин И и К равны 2 (предок у вершины И один – вершина Е, предок у вершины К один – вершина Ж).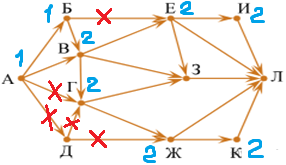
   3.6.индекс З равен 2+2+2=6 (предки вершины З – вершины Е, В и Г).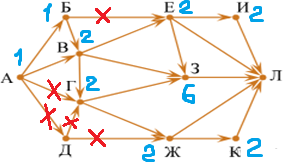
   3.7.индекс вершины Л равен 2+2+6+2+2=14 (предки вершины Л – вершины И, Е, З, Ж и К).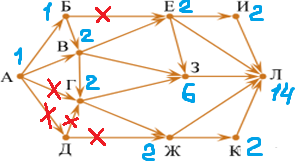

3. Индекс вершины Л – ответ задачи.

4. Ответ: 14.

Решите самостоятельно:

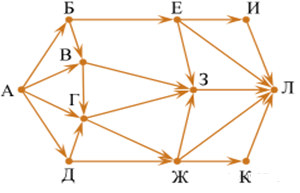
1) На рисунке  — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К и Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л, проходящих через город З?

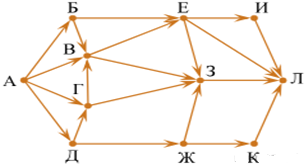
2) На рисунке  — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К и Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л, проходящих через город E?