Алгоритмы математических действий (математика 5 - 7 класс)

Чтобы научить детей самостоятельно учиться и проявлять творчество необходимо применение деятельностного подхода в обучении. Для этого учащихся нужно замотивировать и обучить их приемам и способам учебной деятельности, которые помогут сформировать необходимые знания, умения и навыки.

Применение алгоритмов при изучении математики способствуют умственному развитию и формированию логического мышления.  Знание алгоритмов помогает избежать многих ошибок.

Алгоритм - одно из основных математических понятий. Слово «АЛГОРИТМ» происходит от имени узбекского математика Хорезми (поарабски ал-Хорезми), который в 1Х веке до нашей эры разработал правила четырёх арифметических действий над числами в десятичной системе счисления. Совокупность
этих правил в Европе стали называть «алгоритм». В последствии это слово сделалось собирательным названием отдельных правил определённого вида (и не только правил арифметических действий). 

Алгоритмы арифметических действий:

Алгоритм умножения числа на произведение (сочетательное свойство умножения)

Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

Алгоритм вычитания суммы

Для того чтобы вычесть сумму из числа, можно вначале вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое;

Алгоритм вычитания числа из суммы
Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить второе слагаемое.

Алгоритм умножения числа на произведение (сочетательное свойство умножения)

Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

Алгоритм умножения суммы на число (распределительное тельное свойство умножения относительно сложения)
Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения.

Алгоритм умножения разности на число (распределительное тельное свойство умножения относительно вычитания)

Для того, чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.

Алгоритмы нахождения компонентов:

Нахождение неизвестного слагаемого

Чтобы найти неизвестное слагаемое, надо их суммы вычесть известное слагаемое.

Нахождение неизвестного уменьшаемого

Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.

Нахождение неизвестного вычитаемого
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть и разность.

Нахождение неизвестного множителя
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Нахождение неизвестного делимого
Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Нахождение неизвестного делителя
Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Решение задач с помощью уравнения
1. Прочитать внимательно условие задачи;
2. Записать кратко условие задачи, записав все величины (единицы их измерения) , названные в задаче, установив связи и зависимости между ними;
3.Выбрать неизвестное задачи;
4. Выразить остальные величины задачи, установить связи их с неизвестным задачи;
5. Составить уравнение задачи, обосновав его условием задачи;
6. Решить уравнение;
7. Сделать проверку;
8. Выписать ответ.

Алгоритмы выполнения порядка действий

1. Если в выражении нет скобок, и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
2. Если выражение содержит действия первой (сложение и вычитание) и второй (умножение и деление) ступени и в нем нет скобок, то сначала выполняют действия второй ступени, а потом – действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).

Алгоритмы действий с обыкновенными дробями

Сравнение дробей с одинаковыми знаменателями

а) Выбрать наибольшую дробь с одинаковыми знаменателями ту, у которой больше числитель;
б) Выбрать наименьшую дробь с одинаковыми знаменателями ту, у которой меньше числитель.

Сокращение дробей

Для того чтобы сократить дробь необходимо и числитель и знаменатель дроби разделить на их общий делитель, отличный от 1.

Сложение и вычитания дробей с одинаковыми знаменателями

а) При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатели оставляют тот же;
б) При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатели оставляют тот же.

Алгоритм приведения дробей к общему знаменателю
Чтобы привести дроби к наименьшему общему знаменателю надо:
1. найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2. разделить наименьший общий множитель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель;
3. умножить числитель и знаменатель каждой дроби на её дополнительный множитель;

Сложение и вычитания дробей с разными знаменателями

Если знаменатели разные, то:

1) приводим дроби к общему знаменателю, то есть подбираем наименьшее число, которое делится на знаменатели всех дробей;

2)для каждой дроби находим дополнительные множители: для этого общий знаменатель делим на знаменатель той дроби, у которой находим дополнительный множитель;

3)  числитель каждой дроби умножаем на дополнительный множитель;

4)  складываем или вычитаем дроби с одинаковыми знаменателями

Представление смешанного числа в виде неправильной дроби

1. Умножить его целую часть на знаменатель дробной части;
2. К полученному произведению прибавить числитель дробной части;
3. Записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.

Умножение обыкновенных дробей

1)  Записываем под общей чертой, то есть числитель умножить на числитель, знаменатель на знаменатель;

2)  Сокращаем, что можно;

3)  Умножаем.

Деление обыкновенных дробей

1)  Первую дробь переписываем, ставим знак умножения и вторую дробь переворачиваем, то есть, меняем местами числитель и знаменатель;

2)  Выполняем умножение дробей.

Сложение смешанных чисел

1)  Складываем целые части;

2)  Складываем дробные части.

Вычитание смешанных чисел

1)  Вычитаем целые части;

2)  Вычитаем дробные части. Если дробные части не вычитаются, то занимаем из целой части, тогда в числитель первой дроби прибавится число, равное знаменателю и выполняем вычитание.

Умножение смешанных чисел

1. Превращаем смешанные числа или целые числа в неправильные дроби

2. Умножаем по правилу умножения обыкновенных дробей.

Деление смешанных чисел

1)  превращаем смешанные числа или целые числа в неправильные дроби

2)  делим по правилу деления обыкновенных дробей.

Алгоритм нахождения дроби от числа
Чтобы найти дробь от числа, надо умножить число на эту дробь

Алгоритм нахождения числа по его дроби
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.

Алгоритмы действий с десятичными дробями

Сложения (вычитания) десятичных дробей
Чтобы сложить (вычесть) десятичные дроби, нужно:
1. уравнять в этих дробях количество знаков после запятой;
2. записать их друг под другом так, чтобы запятая была записана под запятой;
3. выполнить сложение (вычитание), не обращая внимания на запятую;
4. поставить в ответе запятую под запятой в данных дробях.

Округление десятичных дробей

а) Если первая отброшенная или замененная нулём цифра равна 5, 6,7, 8, 9, то стоящую перед ней цифру увеличивают на 1.
а) Если первая отброшенная или замененная нулём цифра равна 0, 1, 2, 3, 4, то стоящую перед ней цифру оставляют без изменения.

Умножение десятичной дроби на натуральное число

Чтобы умножить десятичную дробь на натуральное число, надо:
1. умножить её на это число, не обращая внимания на запятую;
2. в полученном произведении отделить запятой столько цифр справа , сколько их отделено запятой в десятичной дроби.

Умножение десятичной дроби на 10, 100, 1000, ….

Чтобы умножить десятичную дробь на 10, 100, 1000, … надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоят в множителе после единицы.

Деление десятичных дробей на натуральные числа

Чтобы разделить десятичную дробь на натуральное число, надо:
1. разделить дробь на это число, не обращая внимания на запятую;
2. поставить в частном запятую, когда кончится деление целой части.

Деление десятичной дроби на 10, 100, 1000, ….

Чтобы разделить десятичную дробь на 10, 100, 1000, …надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:
1. выполнить умножение, не обращая внимания на запятые;
2. отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе;
3. если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.

Умножение числа на 0,1; 0,01, 0,001 …

Для того чтобы умножить число на 0,1; 0,01, 0,001 надо:
1. разделить его на 10,100, 1000;
2. перенести запятую на столько цифр, сколько нулей стоит перед единицей в множителе.

Деление числа на десятичную дробь

Для того чтобы разделить число на десятичную дробь, надо:
1. В делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
2. после этого выполнить деление на натуральное число.

Деление числа на 0,1; 0,01, 0,001

Для того чтобы разделить десятичную дробь на 0,1; 0,01, 0,001…, надо:
перенести в ней запятую вправо на столько цифр, сколько в делителе стоит нулей перед единицей ( то есть умножить её на 10, 100, 1000.

Нахождение среднего арифметического

Для нахождения среднего арифметического нескольких чисел надо:
1.найти сумму этих чисел;
2. разделить полученную сумму на число слагаемых;
3. выписать частное в ответ.

Перевод десятичной дроби в проценты :

Чтобы обратить десятичную дробь в проценты надо умножить дробь на 100.

Перевод процентов в десятичную дробь

Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.

Признаки делимости

Признак делимости на 10

Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.

Признак делимости на 5
Если запись натурального числа оканчивается цифрами 0 и 5, то это число делится без остатка на 5.

Признак делимости на 2
Если запись натурального числа оканчивается четной цифрой, то это число четно и делится без остатка на 2.

Признак делимости на 3
Если сумма цифр числа делится на 3, то и число делится на 3.

Признак делимости на 9

Если сумма цифр числа делится на 9, то и число делится на 9.

Признак делимости на 4

На 4 делятся те и только те числа, две последние цифры которого образуют число, делящееся на 4.

Признак делимости на 6

Чтобы число делилось на 6, оно должно делиться на 2 и 3, то есть должно быть чётным и сумма его цифр должна делиться на 3.

Признак делимости на 12

Чтобы число делилось на 12, надо, чтобы оно делилось на 3 и на 4.

И так далее, так можно составить правила деления и на другие числа.

Разложение на простые множители

Нахождение НОД (наибольшего общего делителя)
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:
1. разложить их на простые множители;
2. из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3. найти произведение оставшихся множителей.

Нахождение НОК (наименьшего общего кратного)
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1. разложить их на простые множители;
2. выписать множители, входящие в разложение одного из чисел;
3. добавить к ним недостающие множители из разложений остальных чисел;
4. найти произведение оставшихся множителей.


Арифметические действия с положительными и отрицательными числами

Сложение отрицательных чисел

Чтобы сложить два отрицательных числа, надо:
1. сложить их модули;
2. поставить перед полученным числом знак « - »..

Сложение чисел с разными знаками

Чтобы сложить два числа с разными знаками, надо:
1. из большего модуля слагаемых вычесть меньший;
2. поставить перед полученным числом знак того слагаемого , модуль которого больше.

Нахождение длины отрезка на координатной прямой

Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.

Умножение чисел с разными знаками

Чтобы перемножить два числа с разными знаками, надо:
1.перемножить модули этих чисел;
2. поставить перед полученным числом знак « - ».

Умножение отрицательных чисел

Чтобы перемножить два числа с отрицательными знаками, надо перемножить их модули.

Деление отрицательного числа на отрицательное

Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.

Деления чисел с разными знаками

При делении чисел с разными знаками, надо:
1. разделить модуль делимого на модуль делителя;
2. поставить перед полученным числом знак « - ».

Раскрытие скобок

а) Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».

б) Если перед скобками стоит знак « - », то надо заменить этот знак на « + »,
поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.

Решение линейных уравнений

Чтобы решить линейное уравнение нужно:  

1)  если есть скобки, то раскрываем их по правилу раскрытия скобок;

2)  выражения с буквой переносим в левую часть уравнения , без буквы в правую, меняя знак у числа.

3)  считаем и получаем уравнение вида

ах = в

4)  находим неизвестную букву

х =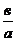 

5) записываем ответ

Алгоритмы действий над одночленами

Запись одночлена в стандартном виде

1. Вычислить произведение числовых множителей (коэффициентов) одночлена и запись его на первом месте.

2. Определить какие переменные входят в одночлен, и записать их в алфавитном порядке.

3. Найти и записать степени переменных.

Умножение одночленов.

Чтобы умножить одночлен на одночлен, надо

1) отдельно умножить их коэффициенты

2)отдельно умножить буквенные множители (степени с одинаковыми основаниями).

Возведение одночлена в степень.

Чтобы возвести одночлен в степень, нужно

1)записать соответствующее выражение;

2)применить свойство возведения произведения в степень;

3)применить свойство возведения степени в степень и вычислить степени чисел.

Алгоритмы действий над многочленами

Алгоритм записи многочлена в стандартном виде

1. Записать все члены многочлена в стандартном виде.

2. Привести подобные слагаемые.

3. Определить степень каждого одночлена и записать их в алгебраическую сумму в порядке убывания степеней.

Сложение и вычитания многочленов

Чтобы найти алгебраическую сумму многочленов, надо

1)записать их в скобках и расставить знаки

2)раскрыть скобки следующим образом: если перед скобкой стоит знак плюс, то знаки членов многочлена не меняются, если перед скобкой стоит знак минус, то знаки членов многочлена меняются на противоположные

3) Приводим получившийся многочлен к стандартному виду.

Умножение одночлена на многочлен

Чтобы умножить одночлен на многочлен, надо

1) умножить этот одночлен на каждый член многочлена

2) полученные произведения сложить.

Умножение многочлена на многочлен

Чтобы умножить многочлен на многочлен, надо

1)каждый член одного многочлена умножить на каждый член другого многочлена

2) полученные одночлены сложить

Алгоритмы применения формул сокращенного умножения

Возведение в квадрат суммы и разности двух выражений.

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения

Возведение в куб суммы и разности двух выражений.

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.  

Умножение разности двух выражений на их сумму

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Разложение разности квадратов на множители

Разность квадратов двух выражений равна произведению их суммы и разности.

Разложение на множители суммы и разности кубов

1) сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

2) разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

Способы для разложения на множители

Выражение можно разложить на множители различными способами:

Вынесение общего множителя за скобки

Чтобы вынести общий множитель за скобки нужно выполнить следующие действия.

Найти число, на которое делятся без остатка числовые коэффициенты каждого одночлена.

Найти буквенные множители, которые повторяются в каждом одночлене. Вынести их за скобку в наименьшей степени.

Вычислить многочлен, который остается в скобках.

Использование формул сокращённого умножения

Многочлен можно разложить на множители с помощью формул сокращенного умножения, записанных в виде:

a2−b2=(a−b)(a+b) (разность квадратов)

a3−b3=(a−b)(a2+ab+b2) (разность кубов)

a3+b3=(a+b)(a2−ab+b2) (сумма кубов)

a2+2ab+b2=(a+b)2 (квадрат суммы)

a2−2ab+b2=(a−b)2 (квадрат разности)

Способ группировки

Способ группировки можно разбить на два этапа:

1) Объединение членов многочлена в группы, имеющие общий множитель, и вынесение из каждой группы общего множителя (в одной из групп общего множителя может не быть).

2) Вынесение полученного общего для всех групп множителя за скобки.

Комбинированный способ

Чтобы разложить многочлен на множители, нужно соблюдать следующий порядок:

1. Вынести общий множитель за скобку. ( Если он есть);

2. Попробовать разложить многочлен на множители по формулам   сокращенного умножения

3. Попытаться  применить способ группировки (если предыдущие не привели к цели).

Алгоритм построения графика функции у=кх

1. Отметить на координатной плоскости Оху точку О с координатами (0;0).

2. Выбрать некоторое значение х₁=0.

3. Вычислить значение у₁=кх₁.

4. Отметить на координатной плоскости Оху точку А с координатами (х₁;у₁).

5. Через точки О и А провести прямую.

1. Выбрать два различных значения х: х₁ и х_{2 .}

2. Вычислить значение у₁=кх₁ +в .

3. Вычислить значение у₂=кх₂+в.

1. Отметить на координатной плоскости Оху точку А с координатами (х₁;у₁).

5. Отметить на координатной плоскости Оху точку В с координатами (х₂;у₂).

1. Через точки А и В провести прямую.