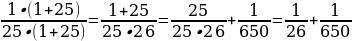| 5 класс В стаде 8 овец. Первая съедает копну за 1 день, вторая – за 2 дня, третья - за 3 дня, …, восьмая – за 8 дней. Кто съест быстрее копну сена: две первые овцы или все остальные вместе? Решение: Первые две овцы за день съедают 1+ 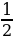 = 1 = 1 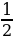 копны сена. Остальные овцы за день съедают ( копны сена. Остальные овцы за день съедают (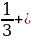 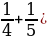 + ( + ( 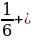 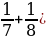 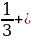 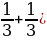 + ( + ( 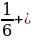 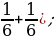 ( (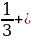 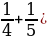 + ( + ( 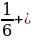 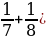 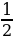 . Значит, копну сена быстрее съедят первые две овцы. . Значит, копну сена быстрее съедят первые две овцы.
6 класс Вычислить значение выражения: 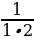 + + 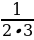 + + 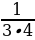 + … + + … + 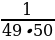 Решение: 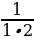 + + 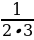 + + 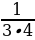 + … + + … + 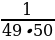 = = 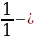 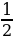 + + 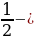 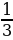 + + 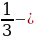 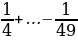 + +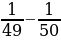 = = 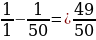 = 0,98 = 0,98
8 класс Соросовская олимпиада: Можно ли написать пять различных дробей, дающих в сумме 1, таких, что их числитель равен 1, а знаменатель – натуральное число. Решение: 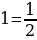 + + 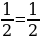 + + 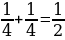 + + 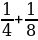 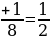 + + 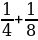 + + 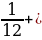 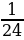
Можно, например, 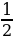 + + 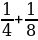 + + 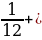 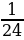 = 1. = 1.
11 класс Задание №19 ЕГЭ: Решить в N числах уравнение: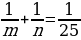 (m n). Решение: Число 25 имеет две пары взаимно простых делителей: 1 и 5; 1 и 25. Разложим аликвотную дробь на сумму аликвотных дробей: 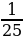 = = 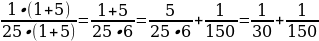 ; ;
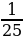 = = 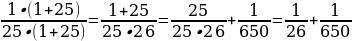
Ответ: m = 150, n = 30 или m = 650, n = 26
ЗА СТРАНИЦАМИ УЧЕБНИКА На машиностроительных заводах есть очень увлекательная профессия разметчик. Разметчик намечает на заготовке линии, по которым эту заготовку следует обрабатывать, чтобы придать ей необходимую форму. Разметчику приходится решать интересные и подчас нелегкие геометрические задачи, производить арифметические расчеты и т. д. Задача: "Понадобилось как-то распределить 7 одинаковых прямоугольных пластинок равными долями между 12 деталями. Принесли эти 7 пластинок разметчику и попросили его, если можно, разметить пластинки так, чтобы не пришлось дробить ни одной из них на очень мелкие части». Решение: Резать каждую пластинку на 12 равных частей - не годилось, так как при этом получалось много мелких долей. Возможно ли деление данных пластинок на более крупные доли? Оказывается, разметчик представил дробь 7/12 в виде суммы единичных дробей 1/3 + 1/4.
| 






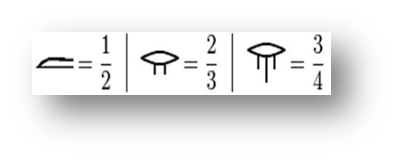



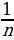 , где n — натуральное число – единичные дроби или аликвотные (от латинского aliquot – «несколько»).
, где n — натуральное число – единичные дроби или аликвотные (от латинского aliquot – «несколько»).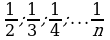
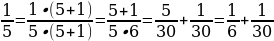 ;
;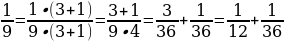
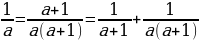
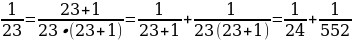
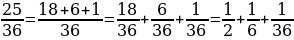
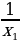 и
и 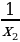 удовлетворяют равенству
удовлетворяют равенству 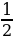 .
. 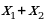 =
= 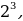 если
если 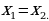
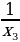 удовлетворяют равенству
удовлетворяют равенству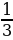 . Тогда
. Тогда 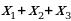 =
= 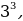 если
если 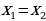 =
= 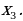
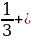
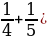 + (
+ ( 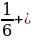
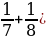
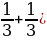 + (
+ ( 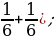 (
(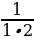 +
+ 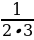 +
+ 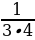 + … +
+ … + 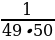
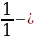
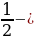
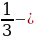
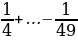 +
+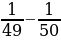 =
= 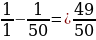 = 0,98
= 0,98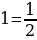 +
+ 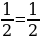 +
+ 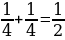 +
+ 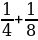
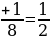 +
+ 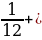
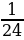
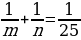
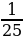 =
= 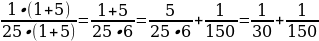 ;
;