Аналитическая справка
по итогам проведения основного государственного экзамена
по математике в 9-х классах 2018 года
В соответствии с приказом Министерства образования и науки Российской Федерации от 10 ноября 2017 г. № 1098 "Об утверждении единого расписания и продолжительности проведения государственного выпускного экзамена по образовательным программам основного общего и среднего общего образования по каждому учебному предмету, перечня средств обучения и воспитания, используемых при его проведении в 2018 году" (зарегистрирован Минюстом России 06.12.2017, рег. № 49127) проведен основной государственный экзамен по математике в 9-х классах.
Основной целью экзамена является государственная (итоговая) аттестация девятиклассников и получение на ее основе информации о состоянии математической подготовки выпускников. С другой стороны, структурные и содержательные особенности экзаменационной работы позволяют дифференцировать учащихся по уровню подготовки с целью определения возможностей для получения дальнейшего образования, в частности для комплектования профильных классов.
Характеристика состава участников экзамена
В 2018 году в экзамене по математике приняли участие 31 выпускник 9-х классов.
Анализ результатов выполнения экзаменационных работ
Краткая характеристика экзаменационной работы
Назначение экзаменационной работы – оценить уровень общеобразовательной подготовки по математике выпускников основной школы общеобразовательных учреждений с целью их государственной (итоговой) аттестации. Результаты экзамена могут быть использованы при приеме учащихся в профильные классы общеобразовательных учреждений и учреждения среднего профессионального образования.
Содержание экзаменационной работы определяется на основе Федерального компонента государственного стандарта основного общего образования по математике (Приказ Минобразования России от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального, общего, основного общего и среднего (полного) общего образования»). КИМ разработаны с учетом положения, что результатом освоения основной образовательной программы основного общего образования должна стать математическая компетентность выпускников, т.е. они должны овладеть специфическими для математики знаниями и видами деятельности, научиться преобразованию знания и его применению в учебных и внеучебных ситуациях, сформировать качества, присущие математическому мышлению, а также овладеть математической терминологией, ключевыми понятиями, методами и приемами.
Работа состоит из двух модулей: «Алгебра», «Геометрия». В модули «Алгебра» и «Геометрия» входит две части, соответствующие проверке на базовом и повышенном уровнях, При проверке базовой математической компетентности учащиеся должны продемонстрировать: владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств, приемов решения задач и пр.), умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.
Части 2 модулей «Алгебра» и «Геометрия» направлены на проверку владения материалом на повышенном уровне. Их назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленную часть выпускников, составляющую потенциальный контингент профильных классов. Эти части содержат задания повышенного уровня сложности из различных разделов курса математики. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности – от относительно более простых до сложных, предполагающих свободное владение материалом курса и хороший уровень математической культуры.
Модуль «Алгебра» содержит 17 заданий: в части 1- 14 заданий, в части 2 - 3 задания.
Модуль «Геометрия» содержит 9 заданий: в части 1 - 6 заданий, в части 2 - 3 задания.
Всего: 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня.
Таблица 1
Результаты экзамена по пятибалльной шкале
|
| Всего | 5 | 4 | 3 | 2 | Успев | Качество | СОУ | Ср. балл |
| 9А | 20 | 0 | 2 | 18 | 0 | 100 | 10 | 38,8 | 3,1 |
| 9Б | 11 | 0 | 2 | 9 | 0 | 100 | 18 | 41 | 3,1 |
| итого | 31 | 0 | 4 | 27 | 0 | 100 | 36 | 40 | 3,1 |
Данные таблицы позволяют сделать вывод, что процент успеваемости составляет 100%, а процент качества (т.е. процент полученных «4» и «5») – 36%.
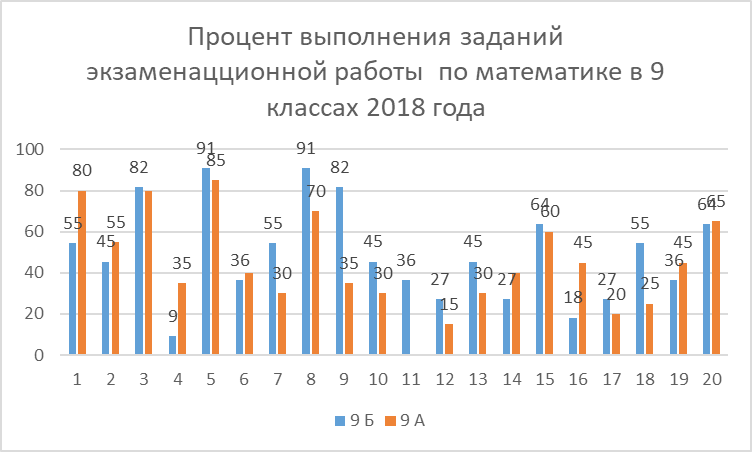
Таблица 2
Максимальное количество баллов, которые можно получить за работу 32 баллов
Лучшие результаты экзамена (18- 20 баллов)
| № п/п | Фамилия, имя | Класс | Количество баллов |
| 1 |
| 9А | 20 |
| 2 |
| 9А | 18 |
| 3 |
| 9Б | 18 |
Самый низкий результат:
| № п/п | Фамилия, имя | Класс | Количество баллов |
| 1 |
| 9А | 3 |
| 2 |
| 9А | 3 |
| 3 |
| 9Б | 3 |
Таблица 3
Сопоставление результатов экзамена и школьной итоговой отметки
| Предмет | Кол-во участников | Кол-во обуч-ся, понизивших школьные отметки на 1 балл | Кол-во обуч-ся, повысивших школьные отметки на 1 балл | Кол-во обуч-ся, подтвердивших школьные отметки |
| Математика | 31 | 3(10%) | 0(0%) | 28(90%) |
Данные таблицы свидетельствуют об объективной оценки знаний учащихся учителем.
Полученные показатели трудности (процент правильных ответов) заданий обязательной части находятся в пределах от 0% до 91%.
В обязательной части экзаменационной работы учащимся предлагались задания по всем содержательным линиям школьного курса алгебры и геометрии основной школы:
Числа и вычисления;
Алгебраические выражения;
Уравнения и неравенства;
Числовые последовательности;
Функции и графики;
Геометрические фигуры и их свойства;
Треугольник;
Многоугольник;
Окружность и круг;
Измерение геометрических величин;
Затруднения у выпускников вызывают задачи, где необходимо было найти процент от числа. Традиционно тема «Проценты» считается трудной для учащихся. Очевидно, это происходит в силу того, что навыки решения простейших задач на проценты отрабатываются в школе крайне мало в силу особенностей расположения материала в учебниках (в 5-6 классах).
По разделу «Тождественные преобразования» сложности возникли при решении задания, связанного с преобразованием выражений, содержащих арифметический квадратный корень. Типичные ошибки при выполнении такого рода заданий заключаются в незнании свойств корней (формул).
При решении задач по теме «Неравенства» трудности у школьников вызвало графическое решение квадратного неравенства. Сложности при выполнении задания были связаны с тем, что учащиеся затрудняются в переводе аналитически заданного неравенства на графический язык.
Раздел «Последовательности и прогрессии» вызвал самые большие затруднения из всех заданий. Эта тема очень неоднозначна. С одной стороны, учащиеся в большинстве школ знакомятся только с частными видами последовательностей – прогрессиями, причем это знакомство носит формальный характер, т.к. большинство задач сводится лишь к применению ограниченного набора формул.
В разделе «Функции и графики» сложности возникли с интерпретацией графика реальной зависимости.
Кроме вышеуказанных, можно выделить еще ряд типичных ошибок:
при соотнесении формулы, задающей функцию, и графика;
при применении различных формул (свойства корней, формулы сокращенного умножения);
при выполнении действий с числами, заданными в стандартном виде.
Успешно справились с категорией заданий «Применение знаний в практической ситуации», сравнение десятичных дробей, решение квадратных уравнений, применение диаграмм для решения задачи.
Часть II экзаменационной работы направлена на проверку владения материалом на повышенном уровне. Основная ее цель – более точная дифференциация учащихся по уровню математической подготовки.
Анализируя данные, отметим имеющееся соответствие между уровнем сложности задания и процентом его выполнения, что свидетельствует о том, что вторая часть работы выполняет свою дифференцирующую функцию. Результаты выполнения заданий работы (№21, №22, №23, №24, №25, №26) оказались низкими.
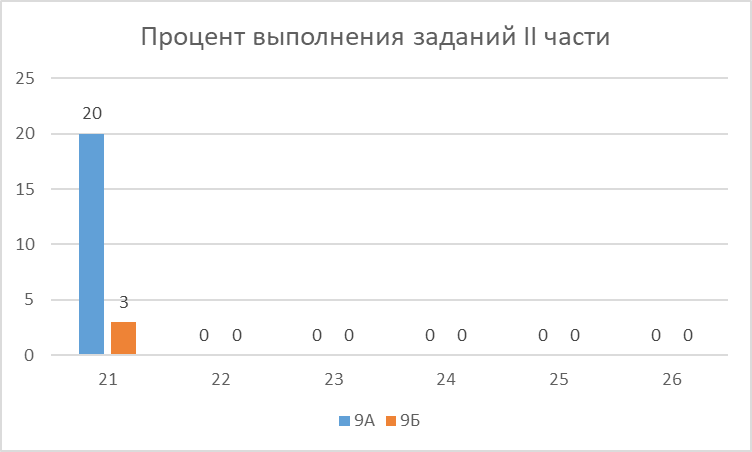
Таблица 4
|
| № | Основные проверяемые требования к математической подготовке | Процент выполнения |
| Раздел «АЛГЕБРА» | 21 | Уметь, решать системы квадратных уравнений
| 20% |
|
| 22 | Уметь строить и исследовать простейшие математические Модели, решать задачи на движение, перевод имкнованных чисел | 0% |
|
| 23 | Уметь выполнять преобразования алгебраических выражений, ре- шать уравнения, неравенства и их системы, строить и читать графи- ки функций, строить и исследовать простейшие математические модели | 0% |
| Раздел «Геометрия» | 24 | Уметь выполнять действия с геометрическими фигурами
| 0% |
|
| 25 | Проводить доказательные рассуждения при решении задач, оцени- вать логическую правильность рассуждений, распознавать оши- бочные заключения | 0% |
|
| 26 | Уметь выполнять действия с геометрическими фигурами, координа- тами и векторами | 0% |
Общие тенденции состояния математической подготовки
Результаты экзамена показывают, что базовая математическая подготовка, составляющая основу общего образования, у учащихся, принимавших участие в государственной (итоговой) аттестации в 9 классе, в целом сформирована.
Так, с заданиями базового уровня сложности, которые проверяют знание основных формул, правил, алгоритмов и умение их применять к решению задач, справляются в среднем около 50% выпускников. Наиболее успешно школьники справляются с заданиями, требующими знаний ограниченного набора математических формул, законов, правил, а также с заданиями, где нужно применить хорошо отработанные алгоритмы решения уравнений, неравенств, преобразования выражений. Задания, в которых требуется интеграция знаний из различных разделов курса алгебры, а также задания, связанные с применением знаний в новой ситуации (в том числе практического характера) вызывают серьезные затруднения у школьников.
На уровне повышенных требований успешно справляются с экзаменационной работой лишь 20% выпускников, сдававших экзамен. Эта группа выпускников, помимо хороших знаний на базовом уровне показывает умение применять эти знания в несколько измененной, новой ситуации.
С заданиями высокого уровня сложности, проверяющими более сложные интеллектуальные и математические умения, выпускники не справились.
Сравнивая результаты основного государственного экзамена с результатами районного пробного основного государственного экзамена следует отметить, что результаты ОГЭ- 2018 намного выше.
Таблица 5
|
| Качество знаний, % | Успеваемость, % |
| Пробный ОГЭ | 52% | 79% |
| ОГЭ-2018 | 36% | 100% |
Общие результаты экзамена показывают, что у школьников в недостаточной мере сформированы:
логическое мышление,
общеучебные умения (сравнение, классификация, умение анализировать информацию),
навыки работы с тестовыми заданиями,
вычислительные навыки;
умение грамотно оформить решение.
Эти проблемы связаны с тем, что учителя много времени и внимания уделяют на отработку алгоритмов решения заданий стандартного характера («решите уравнение», «решите неравенство», «упростите выражение» и т.д.), т.е. «натаскивают» учеников на определенные типы заданий, на определенные формулировки. В то же время на уроках недостаточно внимания уделяется решению задач, требующих применения знаний из различных разделов курса алгебры, недостаточно решается задач практического характера, связанных с жизненным опытом выпускников. Недостаточно внимания уделяется развитию общеучебных умений и умений записывать и оформлять решение.
Результаты экзамена позволили выявить элементы содержания образования, которые недостаточно усвоены выпускниками. К ним относятся:
Задачи, в условиях которых встречаются проценты;
Графическое решение неравенств;
Графическое решение систем уравнений;
Решение текстовых задач;
Способы задания последовательностей;
Построение графиков различных функций.
Рекомендации
Итоги проведения экзамена по математике для выпускников основной школы позволяют высказать некоторые рекомендации, направленные на совершенствование процесса преподавания алгебры и геометрии.
Администрации образовательного учреждения необходимо:
обеспечить проведение анализа итогов экзамена в соответствии с разработанными критериями. Этот анализ будет способствовать планированию управленческих действий, направленных на повышение качества результата.
обеспечить организацию и проведение независимой экспертизы знаний учащихся по математике в течение учебного года, в целях более объективной оценки качества образовательного процесса.
составить план подготовки выпускников к государственной (итоговой) аттестации в 2019 году;
учителям математики необходимо:
проанализировать результаты экзамена по математике в 2018 году;
на семинарах продолжить знакомство педагогов с нормативно-правовыми, организационными, содержательными особенностями экзамена; осуществлять знакомство с критериями оценивания работ выпускников; осуществлять разбор наиболее сложных заданий, предлагавшихся в рамках экзамена.
Учителям математики необходимо:
при годовом планировании уроков отводить достаточное количество времени на организацию повторения материала основной школы;
при проведении текущих и итоговых проверок знаний учащихся чаще использовать материалы и инструментарий, используемые в рамках новой формы проведения экзамена;
совершенствовать формы и методы проведения учебных занятий, использовать возможности для организации индивидуального и дифференцированного обучения школьников;
продумать систему работы со школьниками, имеющими разный уровень математической подготовки;
чаще использовать тестовые технологии при организации обучения математике;
изыскивать возможности для осуществления дополнительной подготовки выпускников через систему уроков, а также через курсы по выбору учащихся. Использование курсов по выбору, направленных на формирование умений решать задачи высокого уровня сложности, будет обеспечивать более качественную подготовку выпускников с хорошей алгебраической подготовкой;
активнее использовать информационно-коммуникативные технологии при проведении учебных занятий и при подготовке к экзамену;
перенести акцент со знаниевого компонента на проверку овладения ключевыми предметными компетенциями; развивать практическую математическую компетентность выпускников;
составить открытый перечень требований к математической подготовке учащихся 9 класса и образцы заданий, конкретизирующих эти требования, с целью знакомства всех категорий выпускников с особенностями содержания проверки;
больше внимания уделять не только отработке стандартных алгоритмов решения задач, но и формированию умений применять знания для решения задач в несколько измененной или новой для ученика ситуации; чаще использовать задачи практического содержания;
больше внимания уделять развитию общеучебных умений и навыков учащихся: умение находить и анализировать информацию, умение работать с различными источниками информации; умение найти более рациональный способ решения, умение осуществлять самоконтроль при решении примеров и задач;
больше внимания уделять развитию самостоятельности мышления учащихся, что будет способствовать формированию умений решать задачи и, в конечном итоге, повышению качества математического образования;
при организации и проведении уроков обязательно обращать внимание на оформление решений. Здесь главным критерием должна служить математически грамотная запись решения;
при подготовке к экзамену обязательно изучить демоверсию и планировать повторение с учетом наиболее сложных тем;
познакомить школьников с критериями оценивания экзаменационных работ в рамках новой формы государственной (итоговой) аттестации;
с учетом выявленных пробелов в математической подготовке школьников, следует более тщательно подходить к изучению таких элементов содержания, как:
решение текстовых задач;
интерпретация графиков реальных зависимостей;
графическое решение уравнений, неравенств и систем;
числовые последовательности и способы их задания;
задачи с параметрами и модулями.


















